
Билет 23.
1
. Градиент функции нескольких переменных,
его свойства.Градиентом
функции
 называется
называется
 ,
,
един.векторы.Теорема
3.5. Производная
функции
един.векторы.Теорема
3.5. Производная
функции
 по направлению вектора
по направлению вектора
 равняется проекции градиента этой
функции на это направление, т. е.
равняется проекции градиента этой
функции на это направление, т. е. .Проекция
некоторого вектора
.Проекция
некоторого вектора
 на направление вектора
на направление вектора
 равняется
равняется .
.
един.вектор, совп. по направлению с
.
един.вектор, совп. по направлению с
.

 .Свойство
1. Производная
функции
.Свойство
1. Производная
функции
 по направлению вектора
по направлению вектора
 достигает своего наибольшего значения,
если направление вектора
совпадает с направлением градиента
этой функции.
достигает своего наибольшего значения,
если направление вектора
совпадает с направлением градиента
этой функции.
Свойство
2. Производная
функции
 по направлению вектора
по направлению вектора
 равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции.
равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции. .
.
2.
Вычисление
двойных интегралов. Перестановка
пределов интегрирования.Пусть
функция
 является непрерывной и ограниченной в
области D.
Область D
ограничена прямыми
является непрерывной и ограниченной в
области D.
Область D
ограничена прямыми
 ,
,
 и кривыми
и кривыми
 ,
,
 ,
,
 Д
Д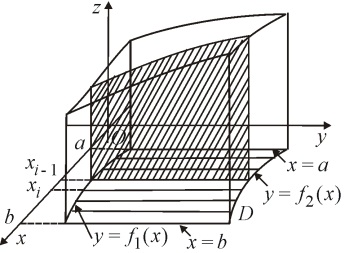 анный
интеграл найдем как объем криволинейного
цилиндра. Отрезок
анный
интеграл найдем как объем криволинейного
цилиндра. Отрезок
 разобьем с помощью произвольно выбранных
точек
разобьем с помощью произвольно выбранных
точек
 на
n
элементарных отрезков длиной
на
n
элементарных отрезков длиной
 ,
i
= 1, 2, …,
n.Через
точки деления
,
i
= 1, 2, …,
n.Через
точки деления
 проведем плоскости параллельно плоскости
Oyz.
Эти плоскости разобьют криволинейный
цилиндр на n
элементарных криволинейных цилиндров.
Найдем площадь каждого сечения
проведем плоскости параллельно плоскости
Oyz.
Эти плоскости разобьют криволинейный
цилиндр на n
элементарных криволинейных цилиндров.
Найдем площадь каждого сечения
 ,
i
= 1, 2, …,
n.Объем
каждого элементарного цилиндра найдем
приближенно как произведение основания
,
i
= 1, 2, …,
n.Объем
каждого элементарного цилиндра найдем
приближенно как произведение основания
 на высоту
на высоту
 .
Получим.
.
Получим. .Объем
всего криволинейного цилиндра приближенно
равен
.Объем
всего криволинейного цилиндра приближенно
равен
 .Перейдем
к пределу при
.Перейдем
к пределу при
 и
и
 ,
получим точное значение объема
криволинейного цилиндра
,
получим точное значение объема
криволинейного цилиндра . Таким
образом, двойной интеграл рассматриваемого
вида находится по формуле
. Таким
образом, двойной интеграл рассматриваемого
вида находится по формуле .Если
область D
ограничена прямыми
.Если
область D
ограничена прямыми
 ,
,
 и кривыми
и кривыми
 ,
,
 ,
,
 ,
то аналогично можно получить формулу
,
то аналогично можно получить формулу
 .Если
область D
ограничена прямыми
,
.Если
область D
ограничена прямыми
,
 ,
,
 ,
,
 ,
то двойной интеграл по этой прямоугольной
области находится по формуле
,
то двойной интеграл по этой прямоугольной
области находится по формуле .При
перестановке пределов интегрирования
интеграл изменяет знак, т. е.
.При
перестановке пределов интегрирования
интеграл изменяет знак, т. е.
 .Для
доказательства используем формулу
Ньютона-Лейбница.
.Для
доказательства используем формулу
Ньютона-Лейбница.
 .
.
3.
Второй признаки сравнения знакоположительных
рядов. Теорема 8.4.
(Третий признак сравнения рядов). 1. Если
отношение последующего члена ряда к
предыдущему для ряда
 не превосходит соответствующего
отношения последующего члена ряда к
предыдущему для сходящегося ряда
не превосходит соответствующего
отношения последующего члена ряда к
предыдущему для сходящегося ряда
 ,
т. е.
,
т. е.
 для любого n,
то ряд
для любого n,
то ряд
 сходится.2. Если же
сходится.2. Если же
 и ряд
и ряд
 расходится,
то и ряд
расходится,
то и ряд расходится. Д о к а з а т е л ь с т в о. По
условию теоремы для любого
n
имеют место неравенства
расходится. Д о к а з а т е л ь с т в о. По
условию теоремы для любого
n
имеют место неравенства
 .Перемножим
почленно левые и правые части этих
неравенств, получим
.Перемножим
почленно левые и правые части этих
неравенств, получим
 .Сократим
одинаковые члены в числителях и
знаменателях левой и правой частях
неравенства, получим
.Сократим
одинаковые члены в числителях и
знаменателях левой и правой частях
неравенства, получим
 .Отсюда
следует, если ряд
.Отсюда
следует, если ряд
 сходится, то по теореме 8.2 (первый признак
сходимости) сравнения рядов также
сходится ряд
сходится, то по теореме 8.2 (первый признак
сходимости) сравнения рядов также
сходится ряд
 ,
так как его члены не превосходят
соответствующих членов сходящегося
ряда
,
так как его члены не превосходят
соответствующих членов сходящегося
ряда
 .
На основании той же теоремы, если ряд
.
На основании той же теоремы, если ряд
 расходится, то и ряд
расходится, то и ряд
 расходится.
расходится.
Билет №24
1.
Непрерывность функции в точке и на
отрезке. Определение непрерывности
функции Пусть
на отрезке [a,
b]
задана функция y
= f(x).
Точки х
и
 принадлежат интервалу (a,
b).
Разность
принадлежат интервалу (a,
b).
Разность
 называется приращением независимой
переменной х
в точке
,
а
называется приращением независимой
переменной х
в точке
,
а
 приращением функции в точке
при данном приращении х
(рис. 9).
приращением функции в точке
при данном приращении х
(рис. 9).
О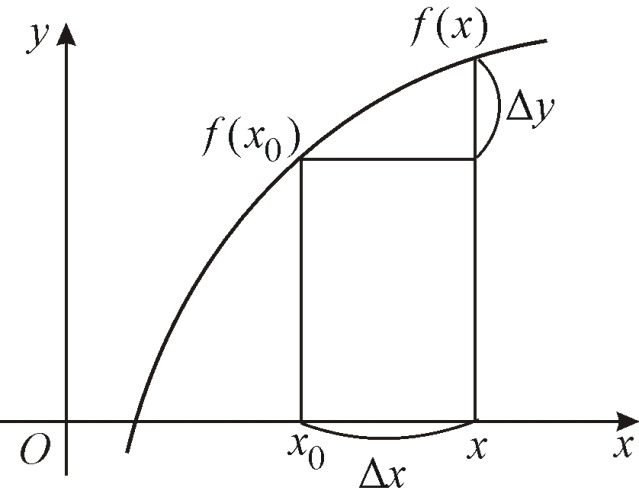 пределение.
Функция
пределение.
Функция
 называется непрерывной в точке
,
если она определена в окрестности этой
точки и бесконечно малому приращению
независимой переменной
называется непрерывной в точке
,
если она определена в окрестности этой
точки и бесконечно малому приращению
независимой переменной
 соответствует бесконечно малое
приращение функции y,
т. е.
соответствует бесконечно малое
приращение функции y,
т. е.
 .Например,
функция y
= С
является непрерывной в любой точке
х(
; +), так как
.Например,
функция y
= С
является непрерывной в любой точке
х(
; +), так как
 .
.
Функция
y
= х
так же является непрерывной в любой
точке х(
; +), так как
 .
.
Преобразуем
условие непрерывности
 .
.
Так
как
 ,
,
 ,
то
,
то
 .
Учитывая это, получим
.
Учитывая это, получим или
или
 .
.
Последнее
равенство можно записать следующим
образом:
 . Таким
образом, если функция непрерывная, то
предел от функции равен функции от
предела независимой переменной, т. е.
можно переходить к пределу под знаком
непрерывной функции.Определение.
Функция
называется непрерывной в точке
,
если она определена в окрестности этой
точки и предел функции в этой точке
равен значению функции в предельной
точке, т. е.
. Таким
образом, если функция непрерывная, то
предел от функции равен функции от
предела независимой переменной, т. е.
можно переходить к пределу под знаком
непрерывной функции.Определение.
Функция
называется непрерывной в точке
,
если она определена в окрестности этой
точки и предел функции в этой точке
равен значению функции в предельной
точке, т. е. .
Определение.
Функция
называется непрерывной на отрезке [a,
b],
если она непрерывна в каждой внутренней
точке этого отрезка и односторонние
пределы функции в граничных точках
равны значениям функции в этих точках,
т. е.
.
Определение.
Функция
называется непрерывной на отрезке [a,
b],
если она непрерывна в каждой внутренней
точке этого отрезка и односторонние
пределы функции в граничных точках
равны значениям функции в этих точках,
т. е.
 ,
,
 .2.
Действия над непрерывными функциями.Теорема
1.11. Если
функции
.2.
Действия над непрерывными функциями.Теорема
1.11. Если
функции
 и
и
 непрерывны в точке
непрерывны в точке
 ,
то в этой точке также непрерывны следующие
функции: 1)
,
то в этой точке также непрерывны следующие
функции: 1)
 ;2)
;2)
 ;3)
;3)
 ,
где
,
где

 . Д
о к о з а т е л ь с т в о. Используем
второе определение непрерывности
функции в точке и свойства пределов,
получим:1)
. Д
о к о з а т е л ь с т в о. Используем
второе определение непрерывности
функции в точке и свойства пределов,
получим:1)
 ;2)
;2)
 ;3)
;3)
 .Так
как пределы от рассмотренных функций
равняются значениям этих функций в
предельной точке, то эти функции
непрерывны.
Непрерывность элементарных функций.1.
Многочлен
.Так
как пределы от рассмотренных функций
равняются значениям этих функций в
предельной точке, то эти функции
непрерывны.
Непрерывность элементарных функций.1.
Многочлен
 является непрерывной функцией, так как
он образован с помощью алгебраических
действий сложения и умножения непрерывных
функций: постоянных коэффициентов
является непрерывной функцией, так как
он образован с помощью алгебраических
действий сложения и умножения непрерывных
функций: постоянных коэффициентов
 и функции y
= х
.
Свойства непрерывных функций.Свойство
1.
Функция y
= f(x)
непрерывная на отрезке [a,
b]
принимает свое наибольшее M
и
наименьшее m
значения
на этом отрезке.Свойство
2.
Функция непрерывная на отрезке хотя бы
один раз принимает любое значение,
заключенное между наименьшим и наибольшим
значениями.Свойство
3.
Если непрерывная функция в граничных
точках отрезка принимает значения
противоположных знаков, то она на этом
отрезке хотя бы один раз обращается в
нуль.Свойство
4.
Если функция y
= f(u)
непрерывна
в точке
и функции y
= х
.
Свойства непрерывных функций.Свойство
1.
Функция y
= f(x)
непрерывная на отрезке [a,
b]
принимает свое наибольшее M
и
наименьшее m
значения
на этом отрезке.Свойство
2.
Функция непрерывная на отрезке хотя бы
один раз принимает любое значение,
заключенное между наименьшим и наибольшим
значениями.Свойство
3.
Если непрерывная функция в граничных
точках отрезка принимает значения
противоположных знаков, то она на этом
отрезке хотя бы один раз обращается в
нуль.Свойство
4.
Если функция y
= f(u)
непрерывна
в точке
 ,
а функция u
= φ
(u)
непрерывна в точке
,
а функция u
= φ
(u)
непрерывна в точке

 ,
то сложная функция
,
то сложная функция
 является непрерывной в точке
является непрерывной в точке
 .
.
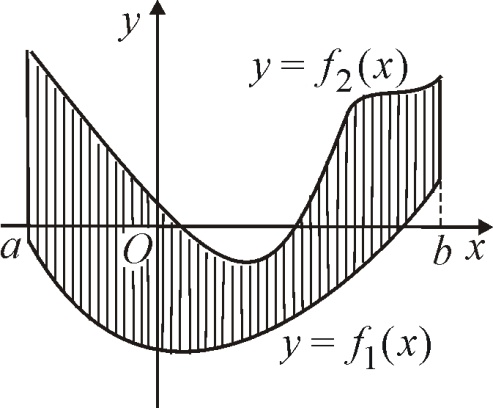
5.10.1. Вычисление площадей фигур.Используем геометрический смысл определенного интеграла.
|
Пусть
требуется найти площадь фигуры,
ограниченной графиками функций
|
В
частном случае, если криволинейная
трапеция ограничена сверху функцией
 ,
а снизу осью Ох
(уравнение y
= 0), то
,
а снизу осью Ох
(уравнение y
= 0), то
|
Если
функции
|
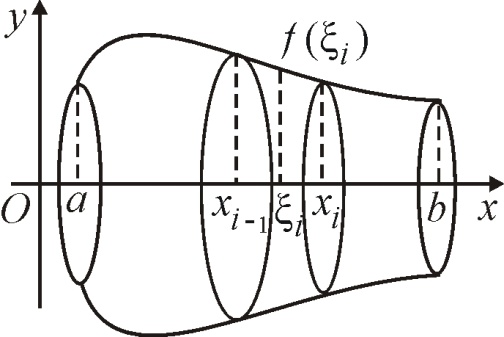
5.10.2. Вычисление объемов тел вращения.
|
Пусть
требуется вычислить объем тела,
образованного вращением вокруг оси
Ох
фигуры,
ограниченной линиями:
|
С
помощью произвольно выбранных точек
 разобьем отрезок
разобьем отрезок
 на n
элементарных отрезков длиной
на n
элементарных отрезков длиной
 i
= 1, 2, …, n.
Через точки деления проведем плоскости
перпендикулярно оси Ох.
Получим n
элементарных объемов тел вращения. На
каждом элементарном отрезке выберем
произвольно точку
i
= 1, 2, …, n.
Через точки деления проведем плоскости
перпендикулярно оси Ох.
Получим n
элементарных объемов тел вращения. На
каждом элементарном отрезке выберем
произвольно точку
 и вычислим значение функции
и вычислим значение функции
 .
Каждое элементарное тело вращения
заменим цилиндром с радиусом основания
и высотой
.
Каждое элементарное тело вращения
заменим цилиндром с радиусом основания
и высотой
 ,
объем которого равен
,
объем которого равен
 .
Объем всего тела вращения приближенно
равен
.
Объем всего тела вращения приближенно
равен
 .Данная
сумма является интегральной. Перейдем
к пределу при
.Данная
сумма является интегральной. Перейдем
к пределу при
 ,
,
 и получим точное значение объема
и получим точное значение объема или
или
 .
.
Если
тело образуется вращением вокруг оси
Оy
фигуры, ограниченной линиями:
 ,
,
 ,
то его объем находится по формуле
,
то его объем находится по формуле .
.


 .Пусть
.Пусть
 .
Тогда площадь фигуры можно найти по
формуле
.
Тогда площадь фигуры можно найти по
формуле .
. .
.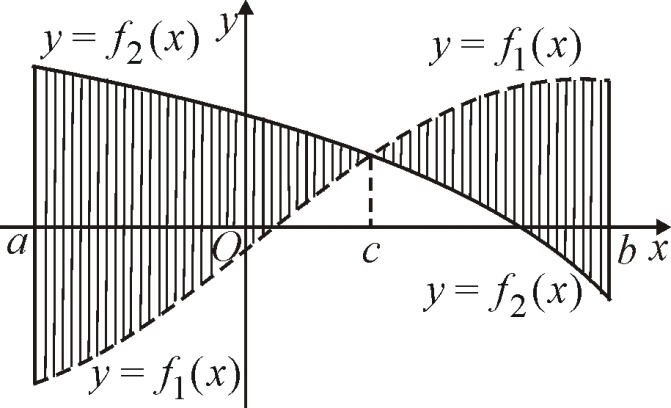
 пересекаются в точке
пересекаются в точке
 ,
так, что при
,
так, что при
 ,
а при
,
а при
 , то
, то
 .
.

 ).
Составим интегральную сумму и перейдем
к пределу
).
Составим интегральную сумму и перейдем
к пределу