
Симплекс метод
Рассмотрим каноническую задачу ЛП:


Р
 ешение
системы
линейных уравнений из системы ограничений
задачи Lk
называется базисным, если система
векторов , соответствующих
ненулевым значениям неизвестных в X0,
является линейной независимой. При
этом, если все координаты X0
неотрицательны , то
такое решение называется опорным.
ешение
системы
линейных уравнений из системы ограничений
задачи Lk
называется базисным, если система
векторов , соответствующих
ненулевым значениям неизвестных в X0,
является линейной независимой. При
этом, если все координаты X0
неотрицательны , то
такое решение называется опорным.
П усть
система ограничений задачи ЛП Lk
приведена к единичному базису и без
ограничения общности имеет следующий
вид:
усть
система ограничений задачи ЛП Lk
приведена к единичному базису и без
ограничения общности имеет следующий
вид:
(1)
З десь
x1, …, xk
– базисные неизвестные, xk+1,
…, xn
– свободные неизвестные.
десь
x1, …, xk
– базисные неизвестные, xk+1,
…, xn
– свободные неизвестные.
С оответственное
базисное решение равно
оответственное
базисное решение равно
Э то базисное решение будет опорным тогда и только тогда, когда все
О порный
план называется невырожденным, если
все
порный
план называется невырожденным, если
все
В ыразим
целевую функцию z(x)
через свободные неизвестные:
ыразим
целевую функцию z(x)
через свободные неизвестные:
Число Dj при свободной неизвестной xj называется оценкой этой неизвестной
К

 ритерий
оптимальности. Опорное решение,
соответствующее системе ограничений
, является оптимальным, если все оценки
свободных неизвестных неотрицательны:
ритерий
оптимальности. Опорное решение,
соответствующее системе ограничений
, является оптимальным, если все оценки
свободных неизвестных неотрицательны:
Критерий неразрешимости. Если существует оценка , такая что в системе (1), то задача Lk неразрешима из-за неограниченности целевой функции.
Запишем задачу Lk в виде следующей таблицы, предполагается, что x1, …, xk – базисные неизвестные.
С |
Б |
x1 |
x2 |
… |
xk |
xk+1 |
… |
xn |
H |
c1 |
c2 |
|
ck |
ck+1 |
|
cn |
|||
c1 |
x1 |
1 |
0 |
|
0 |
g1,k+1 |
|
g1n |
g10 |
c2 |
x2 |
0 |
1 |
|
0 |
g2,k+1 |
|
g2n |
g20 |
|
… |
… |
… |
|
… |
… |
|
… |
… |
ck |
xk |
0 |
0 |
|
1 |
gk,k+1 |
|
gkn |
gk0 |
Z |
0 |
0 |
… |
0 |
Dk+1 |
… |
Dn |
D0 |
|
В
 первом столбце С расположены
коэффициенты при базисных неизвестных
в целевой функции, во втором столбце Б
– базисные неизвестные, следующие
столбцы задают систему ограничений
(1).
первом столбце С расположены
коэффициенты при базисных неизвестных
в целевой функции, во втором столбце Б
– базисные неизвестные, следующие
столбцы задают систему ограничений
(1).
Оценка Dj неизвестной xj находится по формуле:
Э той таблице соответствует базисное решение:
З начение
целевой функции
начение
целевой функции
Переход от одного опорного решения к другому
1 )
Определим среди всех отрицательных
оценок минимальную, т. е. находим
разрешающий столбец q:
)
Определим среди всех отрицательных
оценок минимальную, т. е. находим
разрешающий столбец q:
2 )
Находим отношения свободных членов
к положительным элементам выбранного
столбца; из этих отношений выбираем
наименьшее, т. е. находим разрешающую
строку p:
)
Находим отношения свободных членов
к положительным элементам выбранного
столбца; из этих отношений выбираем
наименьшее, т. е. находим разрешающую
строку p:
3) Из базиса выводим неизвестную xp и вводим вместо нее неизвестную xq.
4
 )
Пересчитываем таблицу по формулам
)
Пересчитываем таблицу по формулам

5) Для полученного нового опорного решения проверяем признак оптимальности и признак неразрешимости.
ТРАНСПОРТНАЯ ЗАДАЧА.
Задача: Однородный груз, имеющийся в m пунктах отправления (производства) в количествах а1, а2, ..., аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) в количествах b1, b2 ..., bn единиц. Стоимость перевозки (тариф) единицы продукции из i-ого пункта отправления в j-ый пункт назначения составляет cij (i=1,…,m; j=1,…,n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится, и запросы всех пунктов потребления удовлетворяются.

П усть
xij – количество
груза перевозимого с i-ого пункта
отправления (ПО) в j-ый пункт назначении
(ПН).
усть
xij – количество
груза перевозимого с i-ого пункта
отправления (ПО) в j-ый пункт назначении
(ПН).
Матрица – план перевозок.
П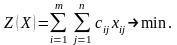
 роизведение
cij×xij
определяет затраты на перевозку груза
с i-ого ПО в j-ый
ПН. Тогда суммарные затраты на перевозку
груза равны . По условию
задачи необходимо обеспечить
роизведение
cij×xij
определяет затраты на перевозку груза
с i-ого ПО в j-ый
ПН. Тогда суммарные затраты на перевозку
груза равны . По условию
задачи необходимо обеспечить
минимум суммарных затрат. Следовательно, целевая функция имеет вид:
м атематическая
модель транспортной задачи имеет вид:
атематическая
модель транспортной задачи имеет вид:
В рассмотренной модели транспортной
задачи предполагается, что суммарные
запасы поставщиков равны суммарным
запросам потребителей, т.е.
рассмотренной модели транспортной
задачи предполагается, что суммарные
запасы поставщиков равны суммарным
запросам потребителей, т.е.
Т акая
задача называется задачей с правильным
балансом, а ее модель – закрытой.
Если равенство (2) не выполняется, т.е.
акая
задача называется задачей с правильным
балансом, а ее модель – закрытой.
Если равенство (2) не выполняется, т.е.
то задача называется задачей с неправильным балансом, а ее модель – открытой.
Рассказать про циклы. Набор клеток, из которых нельзя построить цикл называется ациклическим. Для того чтобы допустимое решение было опорным, необходимо чтобы набор базисных клеток таблицы был ациклическим.
Метод Северо-Западного угла
Заполнение таблицы ТЗ начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель.


Xопор.=
Переход от одного опорного решения к другому. Метод потенциалов
Теорема (признак оптимальности опорного решения). Если существуют m чисел u1, u2, …, um и n чисел v1, v2, …, vn такие, что ui+vj=cij для базисных (занятых) клеток и ui+vj£cij для свободных клеток, то план будет оптимальным планом транспортной задачи. Числа ui называются потенциалами пунктов отправления, числа vj называются потенциалами пунктов назначения
Г руппа
равенств ui+vj=cij
для базисных клеток используется
как система уравнений для нахождения
потенциалов. Данная система имеет m+n
неизвестных ui
и vj
( ). Число уравнений равно
m+n-1. Следовательно, чтобы
найти ее решение достаточно задать
значение одной неизвестной произвольно
(например, u1=0),
а остальные найти из системы.
руппа
равенств ui+vj=cij
для базисных клеток используется
как система уравнений для нахождения
потенциалов. Данная система имеет m+n
неизвестных ui
и vj
( ). Число уравнений равно
m+n-1. Следовательно, чтобы
найти ее решение достаточно задать
значение одной неизвестной произвольно
(например, u1=0),
а остальные найти из системы.
Г руппа
неравенств ui+vj£cij
для свободных клеток используется
для проверки оптимальности опорного
решения.
руппа
неравенств ui+vj£cij
для свободных клеток используется
для проверки оптимальности опорного
решения.
Запишем неравенства в виде:
Числа Dij называются оценками свободных клеток таблицы ТЗ.
О ценки
для свободных клеток ТЗ используются
для улучшения опорного решения. С этой
целью находят клетку (l, k)
таблицы, соответствующую max
Dij
( ). Если Dlk£0,
то решение оптимальное. Если Dlk>0,
то соответствующую клетку вводят в
число базисных. Т.к. базисных клеток
стало m+n, то по теореме 2 из них
можно построить цикл. С помощью цикла
улучшают решение. Для этого необходимо
расставить в клетках, которые входят в
цикл знаки «+» и «–» поочередно, начиная
с вновь введенной базисной клетки , в
которую ставится знак «+».В клетках, где
стоит знак «–» выбрать клетку (p,
q) с наименьшей
перевозкой, т.е. . Затем
осуществляют сдвиг по циклу на
величину Q.
ценки
для свободных клеток ТЗ используются
для улучшения опорного решения. С этой
целью находят клетку (l, k)
таблицы, соответствующую max
Dij
( ). Если Dlk£0,
то решение оптимальное. Если Dlk>0,
то соответствующую клетку вводят в
число базисных. Т.к. базисных клеток
стало m+n, то по теореме 2 из них
можно построить цикл. С помощью цикла
улучшают решение. Для этого необходимо
расставить в клетках, которые входят в
цикл знаки «+» и «–» поочередно, начиная
с вновь введенной базисной клетки , в
которую ставится знак «+».В клетках, где
стоит знак «–» выбрать клетку (p,
q) с наименьшей
перевозкой, т.е. . Затем
осуществляют сдвиг по циклу на
величину Q.
Сдвигом по циклу на величину Q называется увеличение объемов перевозок во всех клетках цикла, отмеченных знаком «+», на Q, и уменьшить – во всех клетках цикла, отмеченных знаком «–», на Q. Таким образом, клетка (p, q) выйдет из числа базисных и получаем новое опорное решение.
