6. Поток вектора напряженности электростатического поля. Теорема Остроградского-Гауса.

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

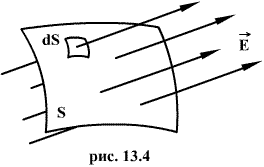
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

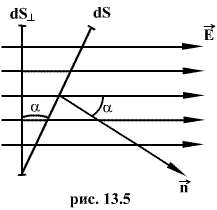
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

где - угол между силовой линией и нормалью к площадке dS; - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

(13.4)

Так как , то

(13.5)

где - проекция вектора на нормаль и к поверхности dS.

7. Напряженность электростатического поля равномерно заряженной сферы.

Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность заряда в любой точке сферы будет одинакова.

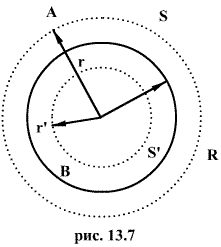
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен

По теореме Гаусса

Следовательно

(13.8)

Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

(13.9)

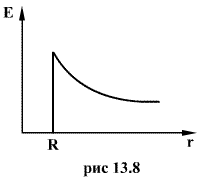
Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. Следовательно, по теореме Гаусса, и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.

8. Напряженность электростатического поля бесконечной равномерно заряженной плоскости.

Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости

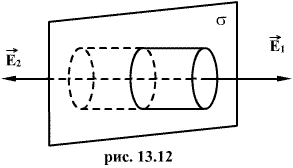
Суммарный поток вектора; напряженности равен вектору , умноженному на площадь S первого основания, плюс поток вектора через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом , С другой стороны по теореме Гаусса

Следовательно

но тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна (13.14)

В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.