Закон Ома в дифференциальной форме.
Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):
В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке.
Сопротивление R участка цепи зависит от длины l этого участка, поперечного сечения S и удельного сопротивления проводника ρ. Зависимость сопротивления от материала проводника и его геометрических размеров выражается формулой:
которая справедлива только для проводников постоянного сечения. Для проводников переменного сечения соответствующая формула не будет столь простой. В проводнике переменного сечения сила тока в различных сечениях будет одинаковой, однако плотность тока будет разной не только в различных сечениях, но даже и в различных точках одного и того же сечения. Различное значение будет иметь и напряженность, а, следовательно, и разность потенциалов на концах различных элементарных участков. Усредненные значения I, U и R по всему объему проводника не дают информации об электрических свойствах проводника в каждой его точке.
Для успешного изучения электрических цепей необходимо получить выражение закона Ома в дифференциальной форме с тем, чтобы оно выполнялось в любой точке проводника любой формы и любых размеров.
Зная
связь напряженности электрического
поля с разностью потенциалов на концах
некоторого участка
, зависимость сопротивления проводника
от его размеров и материала и используя
закон Ома для однородного участка цепи
в интегральной форме
найдем:
Обозначив
где σ — удельная электропроводность
вещества, из которого сделан проводник,
получим:
где
— плотность тока. Плотность тока — это
вектор, направление которого совпадает
с направлением вектора скорости
перемещения положительных зарядов.
Полученное выражение в векторной форме
будет иметь вид:
Оно выполняется в любой точке проводника, по которому течет электрический ток. Для замкнутой цепи следует учесть тот факт, что в ней, кроме напряженности поля кулоновских сил, действуют сторонние силы, создающие поле сторонних сил, характеризующееся напряженностью Ест. С учетом этого закон Ома для замкнутой цепи в дифференциальной форме будет иметь вид:
Разветвленные электрические цепи. Правила Кирхгофа.
Расчет разветвленных цепей упрощается, если пользоваться правилами Кирхгофа. Первое правило относится к узлам цепи. Узлом называется точка, в которой сходится более чем два тока. Токи, текущие к узлу, считается имеют один знак (плюс или минус), от узла - имеют другой знак (минус или плюс).
Первое правило Кирхгофа является выражением того факта, что в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды и формулируется в следующем виде: алгебраическая сумма токов, сходящихся в узле, равна нулю
Второе правило Кирхгофа является обобщением закона Ома на разветвленные электрические цепи.
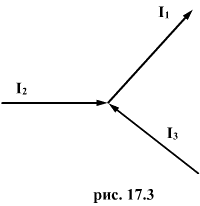
Рассмотрим произвольный замкнутый контур в разветвленной цепи (контур 1-2-3-4-1) (рис. 1.2). Зададим обход контура по часовой стрелке и применим к каждому из неразветвленных участков контура закон Ома.
Сложим эти выражения, при этом потенциалы сокращаются и получаем выражение
В любом замкнутом контуре произвольной разветвленной электрической цепи, алгебраическая сумма падений напряжений (произведений сил токов на сопротивление) соответствующих участков этого контура равна алгебраической сумме эдс входящих в контур.
