Взаимная индукция

Р ассмотрим два неподвижных контура 1 и 2, расположенных близко друг к другу. Если в контуре 1 течет ток силы , он создает через контур 2 пропорциональный полный магнитный поток (на рисунке магнитное поле , создающее этот поток, изображено сплошными линиями). При изменении тока в контуре 2 индуцируется э.д.с.

Аналогичным образом при протекании в контуре 2 тока силой возникает сцепленный с контуром 1 поток (на рисунке магнитное поле , создающее этот поток, изображено штриховыми линиями). При изменении тока в контуре 1 индуцируется э.д.с.

Контуры 1 и 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменениях силы тока в другом называется взаимной индукцией.

Коэффициенты пропорциональности и называются взаимной индуктивностью контуров. Расчеты показывают, что в отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу

Их значение зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей среды. Таким образом, можно не делать различий между и , а просто говорить о взаимной индуктивности контуров. Единицы измерения у них те же, что и у обычной индуктивности (Гн).

Для двух соленоидов, намотанных на один сердечник .

Трансформатор является типичным примером двух связанных контуров. Найдём индуктивность трансформатора и коэффициент трансформации.

Рассчитаем взаимную индуктивность двух катушек, намотанных на общий сердечник.

К огда по левой (первичной) катушке течёт ток I₁, в сердечнике возникает магнитная индукция B и магнитный поток Ф. Магнитное поле тороида равно.

– число витков на единице длины.

Вторую обмотку пронизывает полный магнитный поток (потокосцепление) .

По определению взаимная индуктивность двух катушек равна.

(т.к. ). Тогда получим.

Трансформатор был изобретён русским электротехником Яблочковым в 1876 году для раздельного питания отдельных электрических источников света (свеч Яблочкова).

Рассмотрим коэффициент трансформации.

К левой обмотке подключена переменная э.д.с. ₁. По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней э.д.с. и э.д.с. индукции.

R₁ – сопротивление левой обмотки, его делают малым (например, используют медные провода), и тогда I₁R₁  0. Отсюда получаем.

Во второй обмотке по аналогии можно получить.

Отсюда следует.

В этом выражении – коэффициент трансформации.

Если пренебречь потерями, т.е. положить, что сопротивления обмоток очень малы (близки к нулю), то можно записать.

Энергия магнитного поля

С начала замкнём бесконечно длинный соленоид L на э.д.с. ₀. В цепи установится ток I₀. Затем замкнём соленоид на сопротивление R. В цепи будет течь убывающий ток. При этом будет совершена работа.

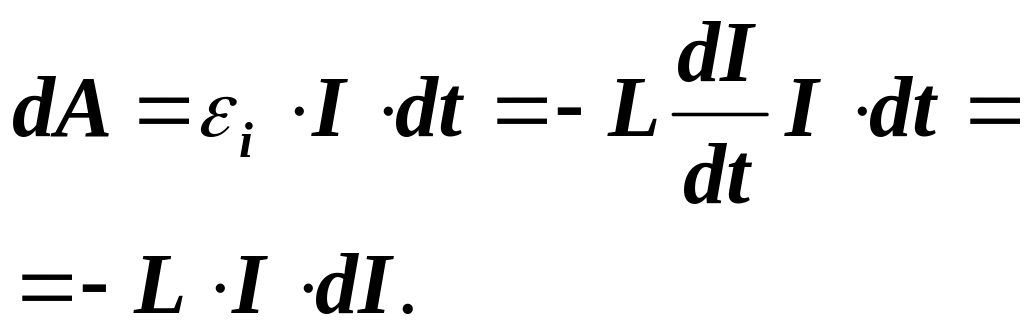
Проинтегрируем и получим выражение для работы.

Работа пошла на нагревание резистора. Откуда взялась эта энергия? Так как других изменений, кроме исчезновения магнитного поля в окружающем пространстве не произошло, то остаётся заключить, что энергия была локализована в магнитном поле соленоида. Следовательно, энергия магнитного поля соленоида равна.

(1)

Подсчитаем энергию магнитного поля через параметры магнитного поля. Для примера рассмотрим соленоид.

, V – объём соленоида.

Подставим эти значения в формулу (1).

Объёмная плотность энергии.

Тогда получим.

Или ещё одно выражение.