Контур с током в магнитном поле

Р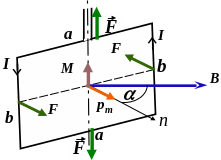 ассмотрим практически важный случай прямоугольного контура (рамки) с током в однородном магнитном поле. Пусть рамка имеет возможность вращаться вокруг оси, проходящей через середины ее сторон длиной а. Поместим рамку перпендикулярно линиям магнитного поля. В рамке протекает ток, направление которого показано на рисунке. Рассмотрим действие сил Ампера на каждую из сторон рамки. Силы Ампера, действующие на стороны контура, направлены в противоположные стороны вдоль оси контура. Действие этих сил сводится только к деформации контура. В зависимости от направления тока к сжатию или растяжению контура. Силы Ампера , действующие на стороны контура, перпендикулярны плоскости, в которой лежат векторы и и направлены так, как это показано на рисунке. Численное значение этих сил можно определить из выражения . Из рисунка видно, что силы, действующие на стороны контура, создают вращающий момент , модуль которого равен

,

где - угол между нормалью к контуру и направлением силовых линий магнитного поля, - плечо силы.

Подставив выражение для силы , получим

Поскольку - это площадь, ограниченная контуром, а это площадь, ограниченная контуром – модуль магнитного момента контура с током, получим выражение вида

.

Запишем это выражение в векторной форме. Магнитный момент контура с током по направлению совпадает с положительной нормалью контура: . Вращающий момент можно записать в виде

(7)

Т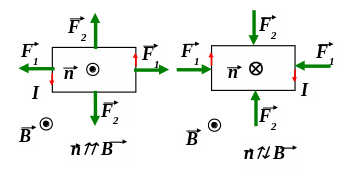 еперь легко определить направление вектора , вспомнив правило: векторы , и образуют правовинтовую ортогональную тройку векторов. Вращающий момент направлен по оси вращения контура, перпендикулярно плоскости, в которой размещаются векторы магнитного момента и магнитной индукции.

П од действием вращающего момента рамка повернётся так, чтобы вектора n и B станут параллельными. На сторону b силы Ампера F₂ действует, растягивая рамку. Так как эти силы равны и противоположны по направлению, то под их действием рамка не смещается. Когда вектора n и B антипараллельны M = 0, так как плечо силы равно нулю, равновесие будет не устойчивым. При незначительном смещении сразу возникнет вращающий момент и рамка повернётся так, чтобы вектора n и B стали параллельными.

Формула (7) применима и к плоскому витку произвольной формы. Кроме того, она может использоваться для расчета вращающего момента контура в неоднородном магнитном поле. В неоднородном поле поведение рамки с током несколько отличается от ее поведения в однородном поле. В неоднородном магнитном поле кроме вращающего момента, стремящегося повернуть рамку, будет действовать сила, вызывающая поступательное перемещение рамки с током. В зависимости от ориентации магнитного момента по отношению к направлению силовых линий магнитного поля контур будет выталкиваться в область более сильного магнитного поля или, наоборот, в область более слабого поля.

Для характеристики магнитного поля используют также поток вектора магнитной индукции.

Угол  это угол между направлением положительной нормали к контуру и направлением вектора магнитной индукции. Единицей измерения магнитного потока является вебер (1 Тлм² = 1 Вб).