3.19 Ферромагнетизм.

3.20 Колебательный контур.

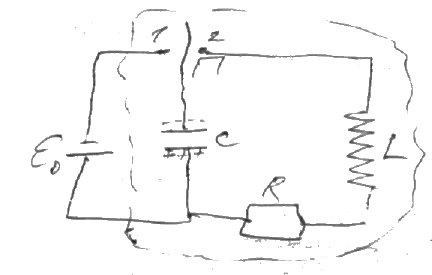Электрическая схема последовательно соединённых конденсатора катушки индуктивности и активного сопротивления R называется колебательным контуром. Если конденсатор зарядить от внешнего источника в положении 1 переключателя П то он накопит энергию где U_m=E₀- амплитуда напряжения на конденсаторе. При переключении П в положение 2 электроны из верхней обкладки через L и R начинают переходить на нижнюю обкладку по цепи пойдёт ток в катушке индуцируется ЭДС самоиндукции поэтому ток возрастает постепенно закон Ома для данной цепи запишется в виде U+E_Si=JR (3) где - Разность потенциалов между обкладками конденсатора, сила тока в цепи связана со скоростью уменьшения заряда конденсатора

из(3) следует или -дифференциальное уравнение изменения заряда на обкладках конденсатора обозначим - коэффициент затухания. - циклическая частота собственных колебаний . . уравнение (6)является уравнением затухающих колебаний. Решение этого уравнения имеет вид где - максимальный заряд на обкладках конденсатора - циклическая частота затухающих колебаний. Если R=0 колебательный контур называется идеальным. Для идеального контура уравнение (6) приобретает вид

уравнение (8) является уравнением гармонических колебаний решение этого уравнения имеет вид . Напряжение на обкладках конденсатора сила тока в цепи обозначим - амплитуда силы тока . Таким образом заряд напряжение и сила тока изменяются в идеальном колебательном контуре изменение по гармоническим законам за ¼ периода сила тока в цепи достигает максимального значения в цепи при этом энергия конденсатора полностью переходит в энергию катушки . однако за счёт ЭДС самоиндукции ток в цепи поддерживается в прежнем направлении, конденсатор перезаряжается нижняя обкладка заряжается отрицательно верхняя положительно к ½ периода ток в цепи прекращается энергия катушки вновь полностью переходит в энергию конденсатора затем конденсатор начинает разряжается в обратном направлении. Таким образом в комбинированном контуре происходит периодический переход энергии электрического поля конденсатора в энергию магнитного поля катушки и наоборот это явление называется электромагнитными колебаниями частота электромагнитных колебаний исходя из(5) - формула Томпсона. В идеальном контуре такие колебания продолжаются бесконечно долго.

3.21 Вынужденные электромагнитные колебания. Резонанс в колебательном контуре

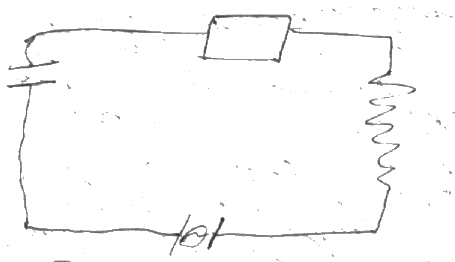В реальном колебательном контуре за счёт наличия активного сопротивления часть энергии выделяется в виде джоулевой теплоты поэтому колебания являются затухающими для обеспечения не затухающих колебаний периодически надо восполнять потерю энергии для этого в колебательный контур вводится источник переменного напряжения называемый звуковым генератором.

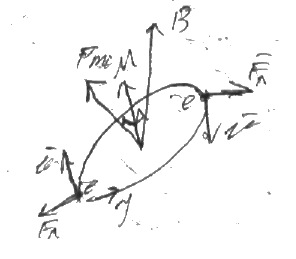Пусть ЭДС генератора – вынуждающее напряжение изменяется по закону E_i =E₀cosΩt;(1) где Ω-циклическая частота вынуждающих колебаний. Тогда закон Ома для контура с генератором запишется в виде U+E_i+E_iS=JR (2) подставив все выражения для соответствующей величины в уравнение (2) получим -дифференциальное уравнение вынужденных колебаний. Это уравнение называется неоднородным дифференциальным уравнением 2-го порядка. Влияние общего решения однородного уравнения только в самом начале работы колебательного контура в дальнейшем изменение заряда J, и определяет изменение и вынуждение поэтому решением (3) для установившегося режима работы относительно J имеет вид

- амплитуда силы тока выражение смещения сдвига по фазе между силой тока и напряжением -реактивное сопротивление -ёмкостное сопротивление индуктивное сопротивление. Как видно из (5) амплитуда J в колебательном контуре является функцией частоты внешнего источника Ω и когда Z_R=0 или амплитуда имеет максимум.

Графически изменение силы тока в зависимости от частоты вынуждающего источника. Резкое увеличение силы тока когда циклическая частота внешнего источника совпадает с собственной частотой контура такое явление называется резонансом колебательного контура. Чем меньше активное сопротивление те острее пик резонансной кривой обычно стремятся уменьшить активное сопротивление. Активное сопротивление это сопротивление проводника и катушки индуктивности при работе колебательного контура между обкладками конденсатора образуется переменное электрическое поле, около катушки переменное магнитное поле с цель ю уменьшить активное сопротивление катушку индуктивности убирают так как сами провода обладают индуктивностью если постепенно приводить к уменьшению емкости и увеличению частоты.

В открытом контуре переменные электрические и магнитные поля от обкладки распространяются во всех направлениях. Распространение в пространстве переменных электрических и магнитных полей называется электромагнитными волнами. Распространение электромагнитных волн можно обнаружить с помощью другого открытия контурного резонатора настроенного с излучателем на резонанс когда волны доходят до резонатора то в искровом промежутке возникает искра.