
- •3.Электромагнетизм
- •3.1 Магнитное поле магнитная индукция закон Ампера
- •3.2 Контур с током в магнитном поле.
- •3.3 Напряжённость магнитного поля.Закон Био-Савара-Лапласа.
- •3.4 Магнитное поле прямолинейного проводника с током
- •3.5 Магнитное поле кругового проводника с током.
- •3.6 Магнитное поле соленоида.
- •3.7 Магнитное взаимодействие токов единица измерения силы тока.
- •3.8 Сила Лоренца движение заряженных частиц в магнитном поле.
- •3.9 Циркуляция вектора напряжённости магнитного поля.
- •3.10 Поток вектора магнитной индукции .Теорема Гаусса для поля .
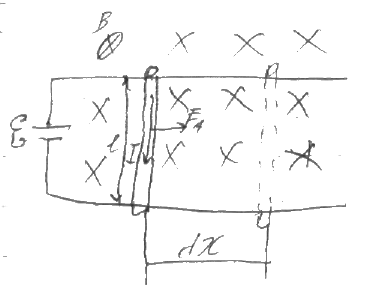
- •3.11 Работа по перемещению проводника и контура с током в магнитном поле.
- •3.12 Явление электромагнитной индукции закон Фарадея Максвелла.
- •3.13 Вращение рамки в магнитном поле.
- •3.14 Индуктивность контура, самоиндукция.
- •3.15 Взаимная индукция. Трансформаторы.
- •3.16 Энергия магнитного поля
- •3.17 Магнитные моменты электронов и атомов.
- •3.19 Ферромагнетизм.
- •3.20 Колебательный контур.
- •3.21 Вынужденные электромагнитные колебания. Резонанс в колебательном контуре
3.8 Сила Лоренца движение заряженных частиц в магнитном поле.

![]()
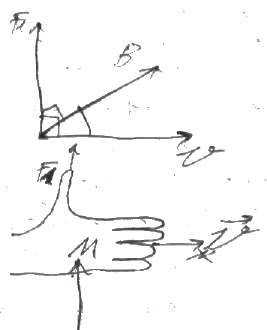 Опыт
показывает что при движении заряженной
частицы в магнитном поле действует сила
называемая силой Лоренца.
Опыт
показывает что при движении заряженной
частицы в магнитном поле действует сила
называемая силой Лоренца.![]() Сила
Лоренца перпендикулярна как скорости
частицы так и магнитной индукции и
направление силы определяется правилом
левой для тройки этих векторов выполняется
векторное произведение
Сила
Лоренца перпендикулярна как скорости
частицы так и магнитной индукции и
направление силы определяется правилом
левой для тройки этих векторов выполняется
векторное произведение![]() .
Сила Ампера является суммой всех сил
действующих на отдельный электрон в
проводнике, также можно показать что
магнитная индукция элемента проводника
с током является суммой магнитных
индукций создаваемых отдельными
частицами
.
Сила Ампера является суммой всех сил
действующих на отдельный электрон в
проводнике, также можно показать что
магнитная индукция элемента проводника
с током является суммой магнитных
индукций создаваемых отдельными
частицами![]() (3)-
Магнитная индукция движущихся заряженных
частиц в произвольной точке М. Формула
(3) легко выводится из закона
Био-Савара-Лапласа. Пусть в однородное
магнитное поле влетает заряженная
частица, на частицу действует сила
Лоренца
(3)-
Магнитная индукция движущихся заряженных
частиц в произвольной точке М. Формула
(3) легко выводится из закона
Био-Савара-Лапласа. Пусть в однородное
магнитное поле влетает заряженная
частица, на частицу действует сила
Лоренца
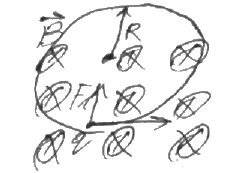
![]() так
как сила Лоренца перпендикулярна
скорости то она не меняется численное
значение скорости, а лишь изменяется
направление движения. То есть FЛ
это центростремительная сила. Под
действием FЛ
частица
движется по окружности радиуса R.
так
как сила Лоренца перпендикулярна
скорости то она не меняется численное
значение скорости, а лишь изменяется
направление движения. То есть FЛ
это центростремительная сила. Под
действием FЛ
частица
движется по окружности радиуса R.
![]() -центростремительная
сила. Приравняв правые части (4) и (5)
-центростремительная
сила. Приравняв правые части (4) и (5)
![]() период обращения
период обращения![]() (7)
(7)
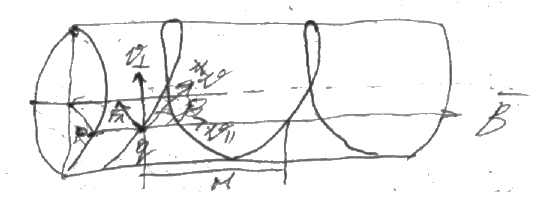
Пусть между скоростью частицы и B уменьшится угол β вектор V можно разложить на 2 составляющие
V┴ =Vsinβ; V║ =Vcosβ ; составляющая параллельная B не меняется а составляющая перпендикулярная B изменяет направление движения согласно предыдущему примеру в результате сложения двух движений траектория приобретает вид спирали, то есть частица движется по поверхности цилиндра радиуса
![]() За
один оборот по направлению вектора B
частица перемещается по направлению
За
один оборот по направлению вектора B
частица перемещается по направлению
![]() если магнитная индукция увеличивается
по ходу движения частицы то согласно(6)
радиус траектории уменьшается таким
образом можно сфокусировать движение
заряженных частиц в узкий пучок.
если магнитная индукция увеличивается
по ходу движения частицы то согласно(6)
радиус траектории уменьшается таким
образом можно сфокусировать движение
заряженных частиц в узкий пучок.
3.9 Циркуляция вектора напряжённости магнитного поля.

![]() Для
электростатического поля циркуляция
напряжённости определяется по формуле
(1) имеет смысл работа перемещения
единичного положительного точечного
заряда вдоль замкнутого контура L
эта работа равна 0 . Силовые поля у которых
циркуляция напряжённости по замкнутому
контуру =0 называются потенциальными.
Напряжённость магнитного поля бесконечно
длинного прямолинейного проводника
Для
электростатического поля циркуляция
напряжённости определяется по формуле
(1) имеет смысл работа перемещения
единичного положительного точечного
заряда вдоль замкнутого контура L
эта работа равна 0 . Силовые поля у которых
циркуляция напряжённости по замкнутому
контуру =0 называются потенциальными.
Напряжённость магнитного поля бесконечно
длинного прямолинейного проводника
![]() -
силовая линия магнитной индукции имеет
вид окружности радиуса R
. Вычислим циркуляцию напряжённости
вдоль силовой линии
-
силовая линия магнитной индукции имеет
вид окружности радиуса R
. Вычислим циркуляцию напряжённости
вдоль силовой линии
![]() как видно циркуляция напряжённости
магнитного поля вдоль контура охватывающего
ток не равна 0. Силовые поля у которых
циркуляция напряжённости вдоль замкнутого
контура не равна 0 называются вихревыми
, магнитное поле вихревое. В таких полях
работа перемещения зависит от формы и
траектории движения поэтому нельзя
вводить понятие потенциала.
как видно циркуляция напряжённости
магнитного поля вдоль контура охватывающего
ток не равна 0. Силовые поля у которых
циркуляция напряжённости вдоль замкнутого
контура не равна 0 называются вихревыми
, магнитное поле вихревое. В таких полях
работа перемещения зависит от формы и
траектории движения поэтому нельзя
вводить понятие потенциала.
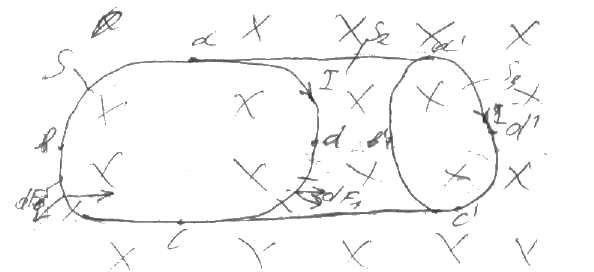
Если контур L
охватывает несколько токов то циркуляция
напряжённости равняется алгебраической
сумме токов охватываемых этим контуром
–Закон полного
тока.
![]() знак + в (2) для J
ставится в том случае если для данного
тока обход по контуру происходит по
правилу правого винта если отдельные
токи контур охватывает несколько раз
то они берутся с соответствующим
множителем
знак + в (2) для J
ставится в том случае если для данного
тока обход по контуру происходит по
правилу правого винта если отдельные
токи контур охватывает несколько раз
то они берутся с соответствующим
множителем![]() .
Магнитное поле торойда . на сердечник
намотано N
круговых витков вычислим циркуляцию
напряжённости радиуса r.
.
Магнитное поле торойда . на сердечник
намотано N
круговых витков вычислим циркуляцию
напряжённости радиуса r.
![]()
