§3 Первообразная.

1.Теорема Морера.

Теорема. Пусть D односвязная область, непрерывна в D и интеграл не зависит от пути интегрирования, или, что тоже, для любой замкнутой кривой Жордана, лежащей в D. Тогда F(z) аналитическая в D и ее производная .

Доказательство.

Рассмотрим две точки z и , путь из z₀ в z обозначим , путь из z₀ в пусть будет , где - отрезок: .

Рис. 4.5.

Тогда

при .

Определение. Функция F(z) такая, что называется первообразной для f(z) на рассматриваемой области.

Теорема. Любые две первообразные одной и той же функции отличаются на константу.

Доказательство. Пусть F₁(z), F₂(z) первообразные для f(z). Положим =F₂ - F₁. Так как  голоморфна, то , кроме того, из условия , следует, что откуда и следует требуемое утверждение.

Напоминание.

Тогда

2.Формула Ньютона-Лейбница

Теорема. Если F(z) первообразная аналитической функции f(z), то

,

в частности, .

Доказательство. Если F(z) – первообразная для функции , то

.

Глава 5. Ряды Тейлора и Лорана

§1 Ряд Тейлора аналитической функции

Напоминание. Равномерно сходящийся на ряд из непрерывных функций можно почленно интегрировать.

1.Теорема Тейлора.

Теорема (Тейлор). Если f аналитическая функция в области D, то для каждой точки z₀ÎD имеет место разложение

R >0 – радиус сходимости ряда, разложение единственно. C – граница некоторой окрестности точки

Доказательство. Пусть меньше, чем расстояние от z₀ до границы .

Рис. 5.1.

Из аналитичности f(z) следует, что для всех лежащих внутри круга ограниченного окружностью C с центром z₀ и радиуса получим: . Так как , то

где .

Ранее отмечалось, что степенной ряд является рядом Тейлора своей суммы, в частности является бесконечно дифференцируемой функцией, таким образом, для его коэффициентов получаем равенство:

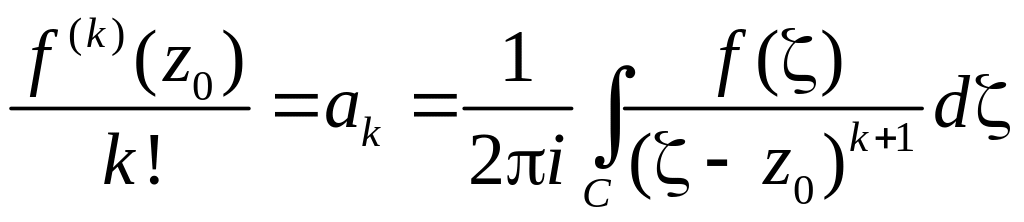. Единственность следует из той же теоремы.

При почленном интегрировании использовалась равномерная сходимость ряда, которая следует из неравенства для .

Следствие. Аналитическая в области D функция f(z) бесконечно дифференцируема в этой области и ее производные вычисляются по формуле

,

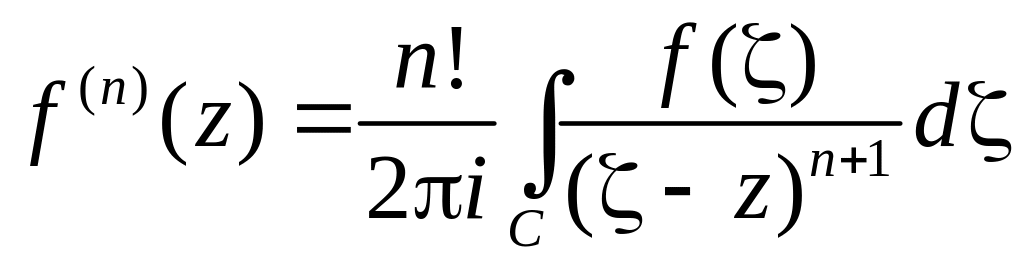где C –контур, содержащий точку z , ограничивающий область .

2.Неравенство Коши для коэффициентов ряда Тейлора. Теорема Лиувилля.

Теорема. Если аналитическая в круге функция f(z) ограничена на окружности , например, , то для коэффициентов a_k в разложении по формуле Тейлора

справедливы неравенства

Доказательство. 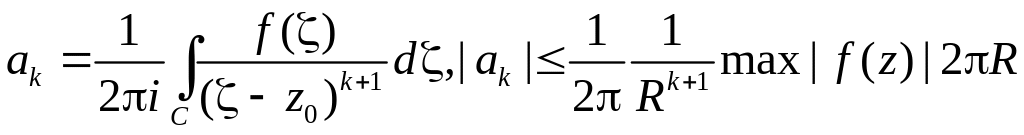, ч.т.д.

Теорема Лиувилля. Если f аналитическая на всей комплексной плоскости и ограничена, то она константа.

Доказательство. Достаточно в неравенстве перейти к пределу при .

§2 Единственность аналитической функции. Принцип максимума модуля.

1.Внутренняя теорема единственности аналитических функций. Нули аналитических функций.

Теорема. Пусть f(z) аналитическая функция, не тождественно равна нулю и f(a)=0, то существует натуральное n , такое, что f(z)=(z - a)ⁿ g(z), где g(z) - аналитическая функция в точке a, не равная нулю в некоторой окрестности точки a. Число n называется кратностью нуля.

Отметим, что для того, чтобы a была нулем кратности n, необходимо и достаточно, чтобы выполнялось условие:

.

Доказательство. Возьмем разложение функции по формуле Тейлора в окрестности точки a:

. Пусть n - индекс первого, отличного от нуля коэффициента a_k :

.

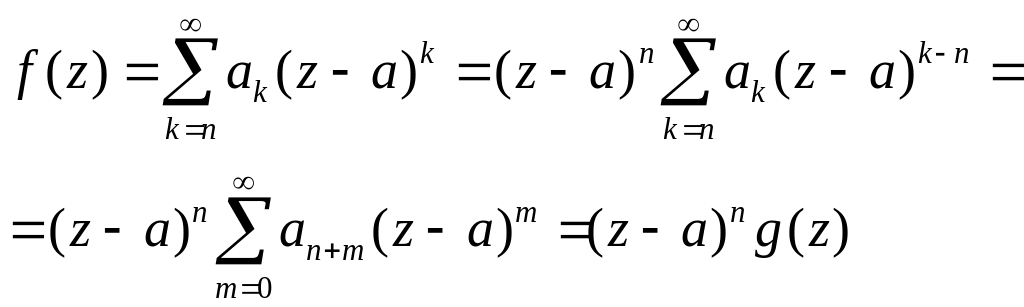Отсюда, в частности, следует

Теорема. Если f(z) аналитическая в точке a, f(a)=0 и не является тождественным нулём, то этот нуль изолирован, то есть, в некоторой окрестности нет других нулей.

Ещё одно следствие.

Теорема. Если f(z) и g(z) аналитические в области D и совпадают на некоторой последовательности точек , то в D.

Для доказательства рассматривается функция h(z) = f(z) – g(z), имеющая a не изолированным нулем. Из предыдущей теоремы следует h(z) 0.

2.Принцип максимума модуля аналитической функции.

Теорема. Если не тождественно постоянная функция f(z) аналитична в односвязной области D и непрерывна в замыкании , то её модуль не может достигать максимального значения в области D. Другими словами, максимальные значения модуля функции могут достигаться аналитической функцией только на границе области.

Доказательство. Предположим противное, пусть . Тогда существует окружность С с центром в z₀, на которой не все значения функции равны M . Иначе функция является постоянной в круге с центром в z₀ , максимально возможного радиуса. Тоже самое можно сказать про любую точку границы этого круга, внутренней по отношению к области D. Таким образом, можно доказать постоянство функции во всей области D . Пусть и , существует некоторая окрестность этой точки на окружности, где |. Длина этого участка окружности пусть будет равна .

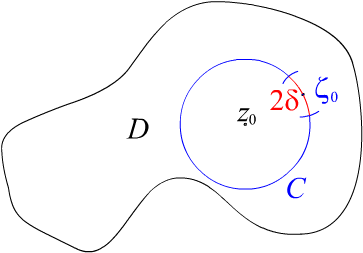
Рис. 5.2.

По теореме о среднем 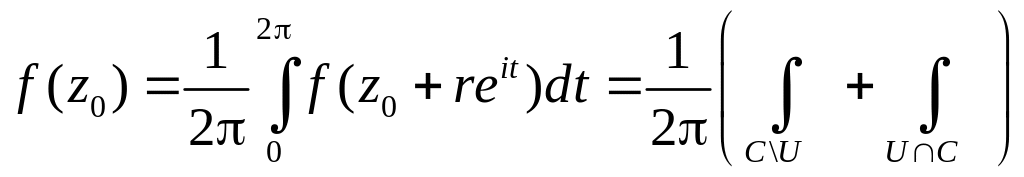. Отсюда

. Получили противоречие.

3.Терема Вейерштрасса

Теорема 1. Если ряд аналитических в области D функций равномерно сходится на любом компакте , то

1. аналитическая в D

2. и этот ряд сходится равномерно на любом компакте, лежащем в области .

Доказательство. Рассмотрим окрестность U точки z₀ , лежащую в D со своим замыканием. Границу U ориентированную положительно обозначим С .

Рис. 5.3.

Сумма ряда непрерывна на C . Рассмотрим интеграл типа Коши

, эта функция аналитична в U и там

, ряд

сходится равномерно на C, следовательно, его можно почленно интегрировать.

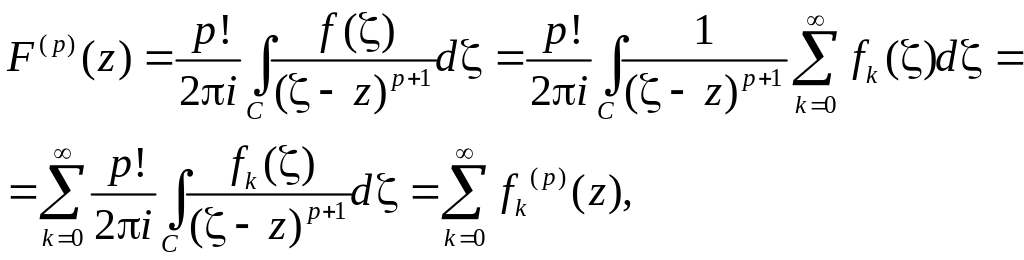
в частности, . В силу произвольности z доказанное утверждение распространяется на все точки из D.

Равномерную сходимость ряда из производных будем доказывать только в частном случае, именно, когда K является замкнутым кругом радиуса r₀, лежащем в D . Несколько увеличим радиус этого круга так, чтобы вновь полученный круг K^* радиуса r также лежал в D . Границу этого круга, ориентированную положительно обозначим C.

Рис. 5.4.

Тогда для всех zK будет выполнено

Откуда и следует требуемое утверждение.

Теорема 2. Если ряд аналитических в области D со спрямляемой границей и непрерывных в замыкании функций f_k(z) равномерно сходится на границе , то этот ряд равномерно сходится и в D. В частности, по теореме 1, сумма этого ряда будет аналитической функцией в области D.

Доказательство будет проведено только для любого компакта лежащего в D и имеющего спрямляемую границу.

Доказательство. Обозначим сумму ряда . Для рассмотрим интегралы типа Коши:

, таким образом, для любого . Пусть компакт и - расстояние от K до границы – длина этой границы. Тогда для всех