Глава 3. Примеры конформных отображений

§1 Дробно линейное отображение

1. Линейная функция.

Можно представить, как суперпозицию отображений: Взаимнооднозначно и конформно отображает на . Первое из этих отображений представляет собой растяжение в |a| раз, второе - поворот плоскости на угол arg a, третье – сдвиг.

Определение. Окружностью в будем называть обычные окружности, либо прямые.

Такие обобщенные окружности можно описать уравнением

.

Указанные условия на коэффициенты можно получить, если привести уравнение этой кривой к каноническому виду: для случая получим окружность В случае получается прямая

Подставляя , получим эквивалентную форму представления окружности или . Ограничения на коэффициенты будет выглядеть так: , где A и E вещественные, .

Круговое свойство. Линейная функция сохраняет окружности.

Действительно, линейная функция представляет собой суперпозицию трех отображений: растяжение, поворот, сдвиг. Не очевидным является только свойство сохранения окружностей при растяжении. Если в уравнение окружности подставить , то получим: или , выполнение условий на коэффициенты легко проверяется и так далее, т. е. снова получаем уравнение окружности. Свойство сохранять обобщенные окружности называется круговым свойством.

2. Преобразование инверсии.

Определение. Точки z, z* называются симметричными относительно окружности на C, если они лежат на луче, выходящем из центра окружности и произведение расстояний от этих точек до центра равно квадрату радиуса. Из условий следует равенство, связывающее симметричные точки относительно окружности с центром в z₀ и радиуса R

или .

Способ построения симметричных точек виден из рисунка.

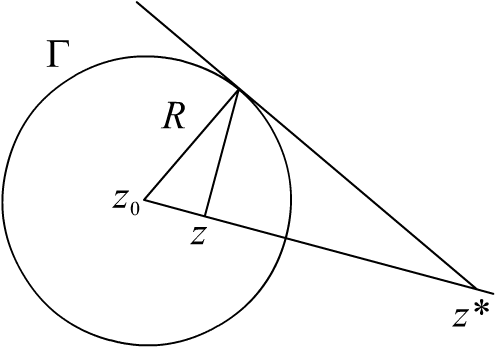
Рис. 3.1.

pic3_1

Через точку проводится луч из центра окружности . Из точки z восстанавливается перпендикуляр к лучу , из точки пересечения перпендикуляра с окружностью проводится касательная до пересечения с лучом в точке . Симметрия точек и следует из подобия двух прямоугольных треугольников: .

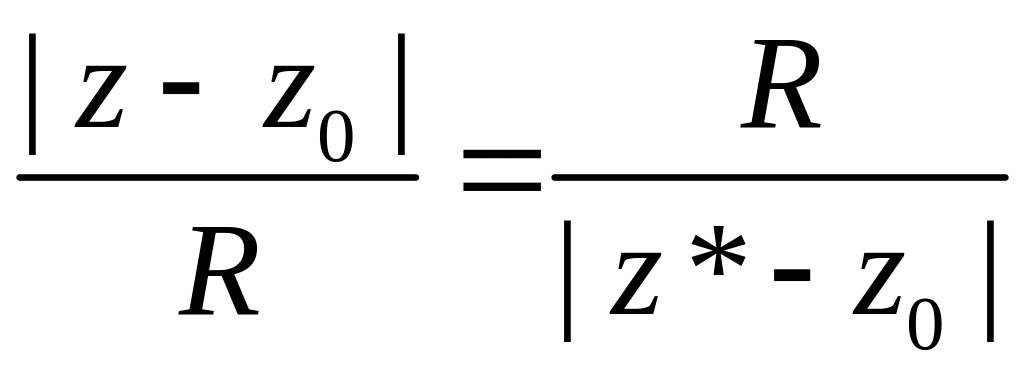Теорема. Для того, чтобы точки z , z* были симметричны относительно , необходимо и достаточно, чтобы любая обобщенная окружность из , проходящая через эти точки, была ортогональна .

Доказательство. Отметим известное свойство касательных и секущих к окружности:

квадрат касательной равен произведению секущей на ее внешнюю часть.

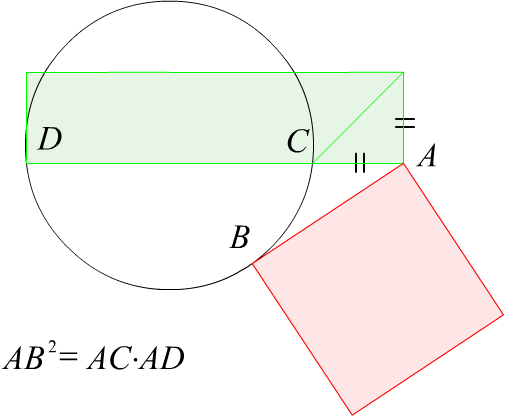
Рис. 3.2.

Необходимость. Дано: z , z* симметричны относительно . Если - прямая, проходящая через z , z* , то и ортогональны. Пусть - некоторая обычная окружность, проходящая через симметричные точки. Проведем одну из касательных к окружности из точки z₀ и обозначим точку касания . Рисунок иллюстрирует это построение.

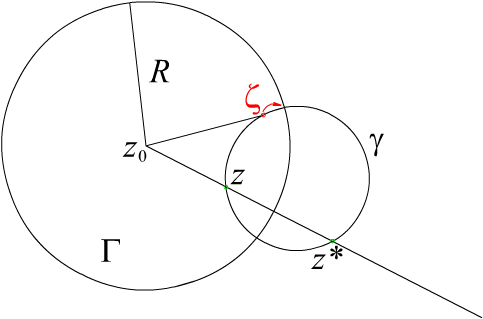
Рис. 3.3.

Если точки симметричны, то по сформулированному свойству секущей, квадрат касательной будет равен , то есть точка должна лежать на окружности . Следовательно отрезок соединяющий z₀ и , с одной стороны будет радиусом к , а с другой стороны касательной к , что означает ортогональность этих окружностей (точка должна быть точкой пересечения и ).

Достаточность. Любая обобщенная окружность , проходящая через z , z* ортогональна . Беря в качестве прямую получим, что точки z, z* лежат на луче, выходящем из центра .

Рис. 3.4.

Проведем какую-нибудь обычную окружность через точки z, z* . Обозначим любую из точек пересечения окружностей через .

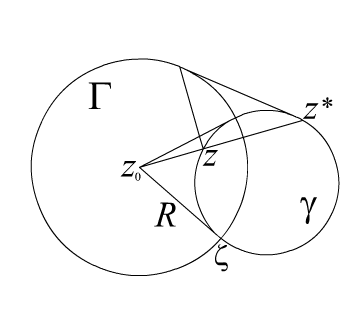
Рис. 3.5.

Так как окружности ортогональны, то отрезок будет касательной для и радиусом для . По упомянутому свойству касательной, получим равенство , следовательно, точки симметричны относительно .

Пример: Инверсия области относительно единичной окружности

pic3_6

Доказанная теорема позволяет сформулировать эквивалентное определение симметричных точек для расширенной комплексной плоскости.

Определение. Точки называются симметричными относительно обобщенной окружности на , если любая обобщенная окружность, проходящая через эти точки, ортогональна к .

Если обобщенная окружность является прямой, то симметрия точек относительно этой прямой совпадает с симметрией относительно прямой в обычном смысле.

Определение. Отображение , переводящее точку в симметричную относительно , называется симметрией относительно окружности или инверсией. При этом мы считаем, что центр переходит в , а в центр окружности.

3. Отображение .

Это отображение обладает круговым свойством. Другими словами, образом обычной окружности или прямой может быть только обычная окружность или прямая. Действительно, пусть дана окружность в : , подставим в это уравнение , получим или или , с теми же условиями на коэффициенты и т.д. (условие , при необходимости, можно обеспечить умножением уравнения на -1).

Отображение является конформным на расширенной комплексной плоскости ( легко проверить в 0 и в бесконечности ).

Следствие. Симметрия может быть реализована как суперпозиция пяти отображений: сдвиг: , операция сопряжения: , обратная: , растяжение: , сдвиг: и поэтому сохраняет окружности и антиконформна. Под антиконформностью понимается то, что направление поворота от одной кривой к другой в точке пересечения меняется при отображении на противоположное.

Примеры - иллюстрации:

pic3_7

pic3_8

4. Дробно линейная функция.

Дробно линейным называется отображение . Матрица называется матрицей дробно линейного отображения. Обычно, мы будем предполагать, что эта матрица не вырождена и . Дробно линейной отображение не изменится, если матрицу «пронормировать», т. е. считать, что . Это отображение можно представить в виде суперпозиции простейших отображений: .

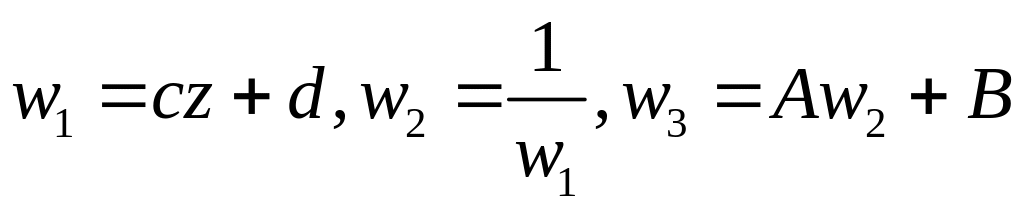Из предыдущих свойств следует, что дробно линейное отображение является конформным на расширенной комплексной плоскости и обладает круговым свойством.

Теорема. Свойство сохранения симметричных точек. Дробно линейное отображение L переводит любые точки , симметричные относительно окружности на , в точки , симметричные относительно образа этой окружности.

Доказательство. Если симметричны относительно , то это означает, что все «окружности» , проходящие через , ортогональны . Так как отображение L сохраняет углы и окружности, то любая окружность, проходящая через , будучи образом некоторой , будет ортогональна , что означает симметрию.

Свойства дробно линейных отображений

1. Дробно линейная функция взаимнооднозначно и конформно отображает всю расширенную комплексную плоскость z на всю расширенную комплексную плоскость w. Обратное отображение так же дробно линейно.

Взамнооднозначность. Разрешим уравнение относительно . . При этом переходит в , а переходит в . Если матрица отображения нормирована, то нормирована и матрица обратного отображения и они взаимно обратны.

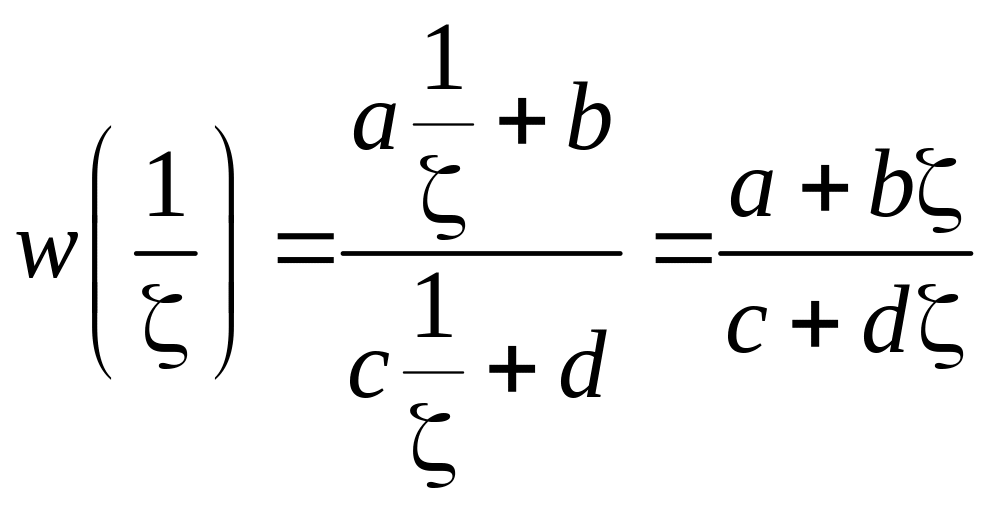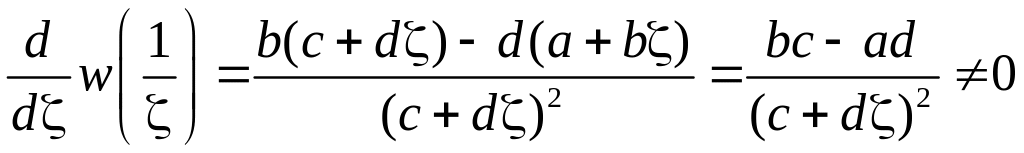Конформность. Производная во всех конечных точках, если . Для проверки конформности в точке рассматривается функция , производная которой в точке . Для проверки конформности в точке рассматривается функция в точке . Производная в точке .

2) Суперпозиция двух дробно линейных отображений есть дробно линейное отображение.

Матрицы этих отображений при суперпозиции перемножаются: если

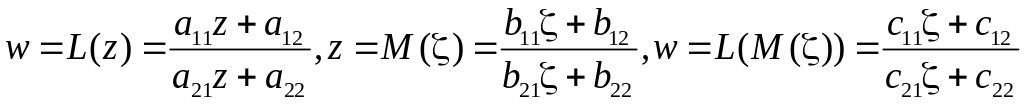, тогда

. Проверяется непосредственно.

3) Круговое свойство и сохранение симметрии. Произвольное дробно линейное отображение L обладает круговым свойством и переводит любые точки , симметричные относительно какой-нибудь окружности на , в точки , симметричные относительно образа этой окружности.

4) Каковы бы ни были три различные точки и три различные точки , существует единственное дробно линейное отображение L такое, что

Доказательство. Рассмотрим отображение , переводящее точки в ,

. Аналогично, отображение

, будет переводить Тогда отображение будет искомым :

Рис. 3.8

Для доказательства единственности, докажем лемму.

Лемма. Если дробно линейное отображение переводит точки 00,  , то оно тождественное.

Доказательство. Пусть Из , ( при этом можно считать, что a=1 ) таким образом, отображение должно иметь вид

Докажем единственность. Предположим, что ещё одна дробно линейная функция w=f(z) обладает этим свойством. Тогда оставляет на месте 0,,1. Такое отображение является тождественным , откуда следует, что .

5) Непосредственной проверкой можно убедиться, что

.

Пример. Найти образы обобщенных окружностей , вещественная и мнимая оси при отображении .

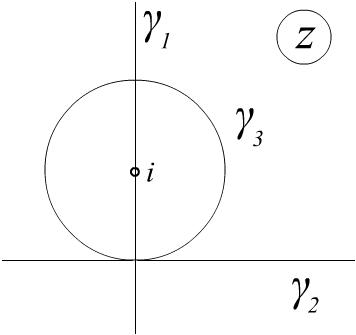
Рис. 3.9.

Замечание. Обобщенная окружность является прямой только тогда, когда она проходит через точку , в противном случае она является обычной окружностью.

В отображается точка , которая принадлежит “окружности” . Это значит, что только является прямой, а будут обычными окружностями. Для того, чтобы нарисовать прямую возьмем любые две симметричные относительно “окружности” точки , например, -1, 1. Эти точки перейдут в симметричные точки относительно . Подставляя значения -1, 1 в найдем образы этих точек .

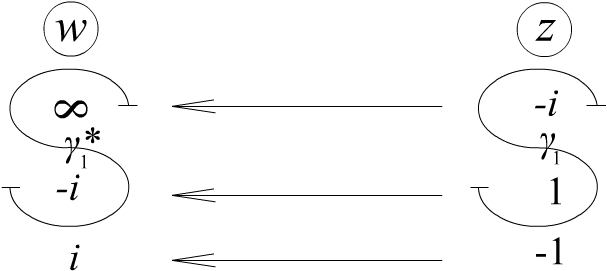
Рис. 3.10.

Рисуем прямую , для которой эти точки являются симметричными

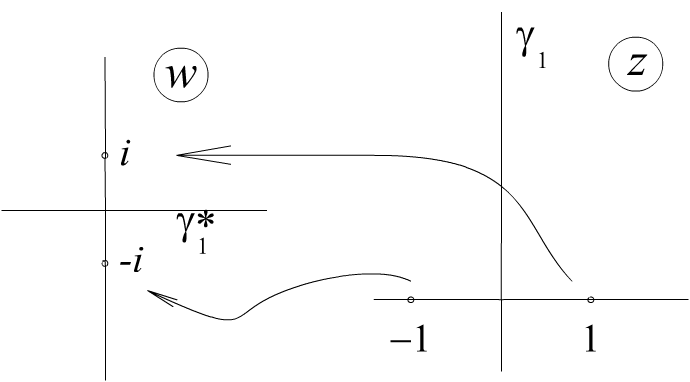
Рис. 3.11.

Для изображения окружностей нужно найти их центры и точки, через которые они будут проходить. Для нахождения центра окружности найдем точку симметричную .

Рис. 3.12.

Центром окружности будет точка . Так как все три кривые пересекаются в 0, а 0 переходит в -1, то будет окружностью радиуса 1.

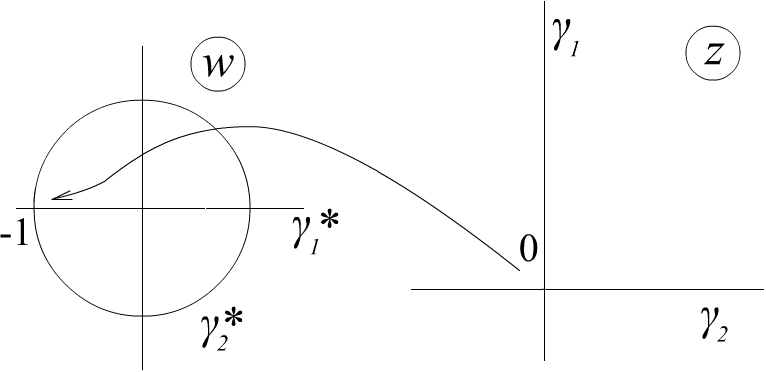
Рис. 3.13.

Тоже самое для окружности . Находим, кто симметричен прообразу .

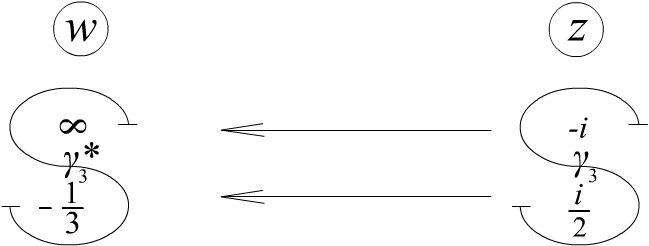
Рис. 3.14.

Точку , симметричную относительно окружности находим из соотношения инверсии.

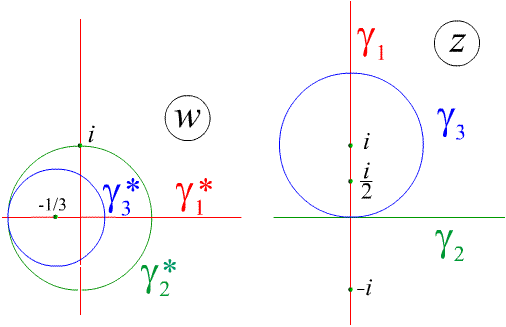
Рис. 3.15.

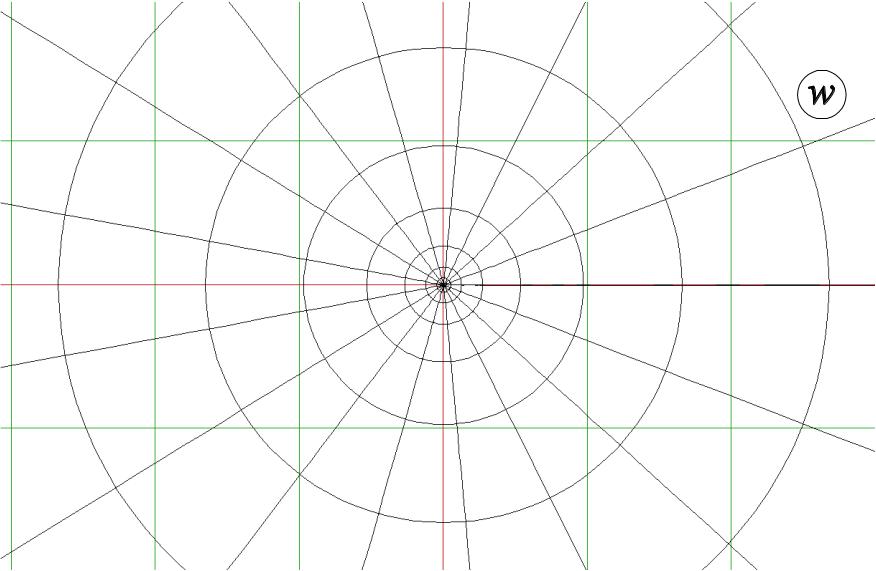
§2 Степенная функция w=zⁿ, n – натуральное.

1.Отображение степенной функцией.

. Область однолистности: для того, чтобы условие однолистности нарушалось в области D, в этой области должна существовать пара различных точек , для которых образы совпадают: . В этом случае и .

Поэтому, если в какой-либо области для различный точек будет выполнено соотношение , то однолистность нарушаться не будет. В частности, каждую из областей функция w=zⁿ отображает однолистно на плоскость С вырезом по положительной части действительной оси.

Пример: . Выбрана область

Рис. 3.16.

pic3_16

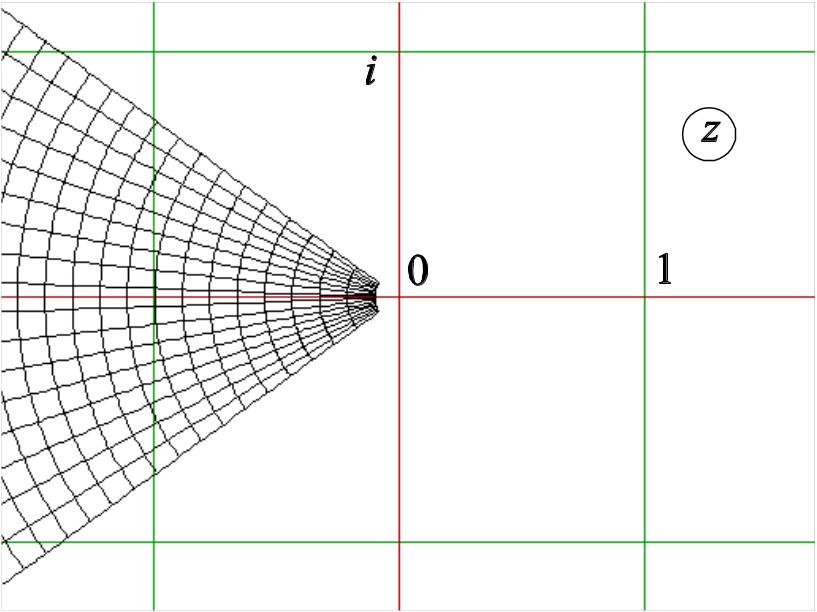
2.Обратная функция.

Определение. Функция f(z) называется однозначной ветвью на множестве D многозначной функции F(z), определённой на D, если f(z) однозначная, непрерывная функция, совпадающая с одним из значений F(z) в каждой точке zD.

Пример: Обратная функция многозначна ( n различных корней, если w0 )

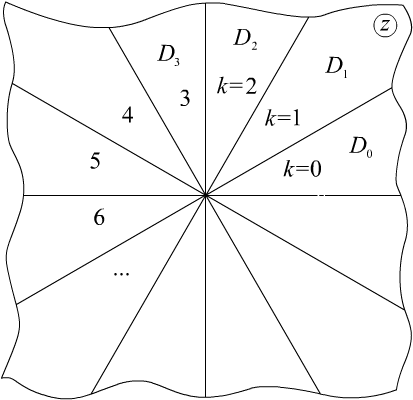
. Рассмотрим n экземпляров плоскости C_w с разрезом по положительной части вещественной оси, будем их обозначать D*_k , k =0,1,…, n – 1. Определим одну из возможных ветвей. Зафиксируем некоторую точку w_kD*_k и для её образа выбираем значение

.

Значение ветви g_k(w) в любой точке будем определять следующим образом: положим

, где получен из непрерывным изменением вдоль какой-либо кривой, соединяющей w и w_k . Можно показать, что конечное значение не будет зависеть от конфигурации пути, поэтому определение корректно.

Рис. 3.17.

pic3_17

В данном случае (удачный выбор областей ) можно было бы не прибегать к услугам кривой , а считать выражение за определение k-ой ветви. Таким образом, можно выделить n однозначных ветвей для функции . Обозначают эти ветви . Ветвь, соответствующая k, есть конформное отображение области D*_k на область

.

Замечание. При отображении , в плоскости w при полном обходе вокруг начала координат arg w получает приращение 2 и мы приходим к другому значению z в плоскости .

Рис. 3.18.

pic3_18

Такие точки (в данном случае, начало координат) называются точками ветвления, точное определение точки ветвления будет дано в следующем пункте. Для степенной функции, кроме 0, точкой ветвления является .

3. Понятие римановой поверхности для функции

Два листа плоскости w склеены, как показано на рисунке. При обходе точкой w по по верхнему листу образ z пройдет полоборота по кривой ₀ в верхней полуплоскости D₀ плоскости z. Продолжаем движение, переходим в месте склейки с верхнего листа на нижний лист на кривую в плоскости w. Далее образ z будет двигаться по ₁ в нижней полуплоскости D₁ плоскости z и полностью завершит оборот, когда точка w вернется на верхний лист по кривой . Поверхность взаимнооднозначно отображается на всю плоскость C_z . Эта поверхность называется поверхностью Римана.

Рис. 3.19.

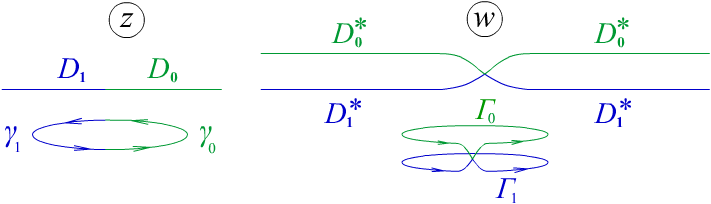
Рис. 3.20.

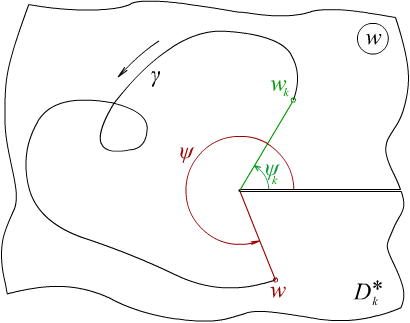
Определение. Если в любой достаточно малой окрестности точки существует замкнутая Жорданова кривая ( можно считать окружностью с центром a), содержащая внутри точку a такая, что при обходе , начиная с точки (и непрерывном изменении модуля и аргумента) значение ветви многозначной функции F(z) переходит в значение другой ветви , то точка a называется точкой ветвления.

Пример. Поверхность Римана для .

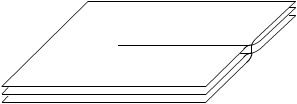
Рис. 3.21.

Рис. 3.22.