
- •Глава 1. Основные понятия
- •§1 Операции над комплексными числами
- •§2 Комплексная плоскость
- •§3 Некоторые понятия, относящиеся ко множествам. Кривые на комплексной плоскости.
- •§4 Функции комплексного переменного
- •§5 Функциональные последовательности и ряды
- •§6 Степенные ряды
- •Глава 2. Аналитические функции. Конформные отображения.
- •§1 Аналитические функции
- •§2 Конформные отображения
- •Глава 3. Примеры конформных отображений
- •§1 Дробно линейное отображение
- •§3 Функция
- •§4 Функция Жуковского
- •§7 Таблица некоторых конформных отображений.
- •Глава 4. Теория интеграла
- •§1. Понятие интеграла. Теорема Коши.
- •§2 Интеграл Коши
- •§3 Первообразная.
- •Глава 5. Ряды Тейлора и Лорана
- •§1 Ряд Тейлора аналитической функции
- •§2 Единственность аналитической функции. Принцип максимума модуля.
- •§3 Ряды Лорана
- •§4 Изолированные особые точки однозначных аналитических функций.
- •Глава 6. Элементы теории вычетов и их использование при вычислении интегралов
- •§1 Вычеты
- •§2. Вычисление интегралов
- •§3 Простейшие классы аналитических функций.
- •Глава 7. Преобразование Лапласа.
- •§1 Преобразование Лапласа.
- •§2 Свойства преобразования Лапласа
- •Глава 8. Приложения.
- •§1 Комплексный потенциал
- •§2 Операционное исчисление
§2 Конформные отображения
Существование обратной функции для аналитической функции в окрестности точки
Пусть f(z) = u(x,y) +iv(x,y) аналитична в точке z0 и f(z0)0
w=f(z): .
.
Якобиан
 в окрестности точки z0.
Следовательно,
в окрестности точки z0.
Следовательно,
![]() имеет
смысл коэффициента искажения площади
в точке
имеет
смысл коэффициента искажения площади
в точке
![]() при
отображении
при
отображении
![]() и
существует
обратная функция в некоторой окрестности
точки
и
существует
обратная функция в некоторой окрестности
точки
![]() , причём
, причём
 .
.
Геометрический смысл аргумента производной.
Пусть
![]() -гладкая кривая Жордана,
-гладкая кривая Жордана,
![]() .Обозначим
.Обозначим
![]() образ кривой
при отображении f.
Предположим, что f(z)
аналитическая в точке z0
функция и
образ кривой
при отображении f.
Предположим, что f(z)
аналитическая в точке z0
функция и
![]() .
.
Имеем
![]() .
Так как при умножении комплексных чисел
аргументы складываются, то
.
Так как при умножении комплексных чисел
аргументы складываются, то
![]()
Если
![]() - главные
значения аргументов,
- главные
значения аргументов,
![]() - угол поворота кривой в точке z0
при отображении w
= f(z),
определяемый с точностью до
- угол поворота кривой в точке z0
при отображении w
= f(z),
определяемый с точностью до
![]() .
Как видим, этот угол не зависит от выбора
кривой, проходящей через данную точку.
.
Как видим, этот угол не зависит от выбора
кривой, проходящей через данную точку.
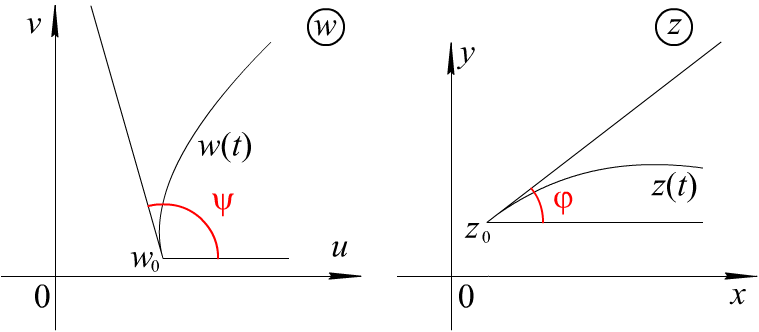
Рис. 2.2.
В
частности, если в плоскости z
пересекаются
две кривые
![]() ,
имеющие в точке пересечения главные
значения аргументов
,
имеющие в точке пересечения главные
значения аргументов
![]() ,
а их образы при отображении w=f(z),
соответственно, углы
,
а их образы при отображении w=f(z),
соответственно, углы
![]() ,
то мы получим
,
то мы получим
![]() ,
откуда,
вычитая одно равенство из другого,
получим
,
откуда,
вычитая одно равенство из другого,
получим
![]() .
Полученное
равенство позволяет сформулировать
следующее
.
Полученное
равенство позволяет сформулировать
следующее
Следствие. При сделанных предположениях (аналитичность в точке и неравенство нулю производной ) углы при отображении сохраняются. Кроме того, сохраняется «порядок обхода». Например, если поворот от касательной к первой кривой в точке пересечения к касательной второй кривой в плоскости z происходит против часовой стрелки, то тоже самое будет наблюдаться и в плоскости w между образами этих кривых.
Пример: . Обратить внимание на сохранение углов и направлений поворота (9 точек пересечений)
pic2_3
Геометрический смысл модуля производной.

Таким
образом,
![]() -коэффициент
линейного растяжения кривой в точке
при заданном отображении.
-коэффициент
линейного растяжения кривой в точке
при заданном отображении.
Коэффициент растяжения кривой в точке, не зависит от кривой, проходящей через эту точку. Это коэффициент равен |f(z0)|. Это свойство называется свойством сохранения масштаба в точке z0. Как уже отмечалось, является коэффициентом растяжения площади в точке z0 при этом отображении.
Пример:
Обратить внимание на изменение площади
при отображении
в окрестности точки
![]() .
Линейные размеры увеличиваются
приблизительно в 2 раза (
.
Линейные размеры увеличиваются
приблизительно в 2 раза (![]() ).
Площадь в 4 раза.
).
Площадь в 4 раза.
pic2_4
Конформные отображения.
Определение (Конформность в C). Непрерывное, взаимнооднозначное отображение w=f(z) области D на область D* называется конформным, если в каждой точке D имеет место
свойство сохранения углов
сохранение масштабов
в перечисленном выше смысле.
Как мы видели, если f(z) аналитична в точке z0 и f(z0), то отображение w=f(z) конформно в некоторой окрестности точки z0.
Определение.
Если две кривые
пересекаются
в бесконечности, например, при
![]() ,
то
углом между кривыми
в
бесконечности называется угол в
0
между
образами этих кривых при отображении
,
то
углом между кривыми
в
бесконечности называется угол в
0
между
образами этих кривых при отображении
![]() ,
то
есть между кривыми
,
то
есть между кривыми
 в
точке
в
точке
![]() .
.
Аналогично,
определяется понятие «изменение линейных
размеров кривой» в бесконечности.
Именно, если
![]() ,
то в
точке
,
то в
точке
![]() изменение
линейных размеров
определяется
по образу кривой
изменение
линейных размеров
определяется
по образу кривой
 .
И
в том и в другом случае
.
И
в том и в другом случае
![]() предварительно
переводится в
0 отображением
.
С учетом этих определений дается
определение конформности в
предварительно
переводится в
0 отображением
.
С учетом этих определений дается
определение конформности в
![]() .
.
Определение (Конформность в расширенной комплексной плоскости ). Непрерывное, взаимно однозначное отображение w=f(z) области D на область D* в называется конформным, если в каждой точке D имеет место
1) свойство сохранения углов
2) сохранение масштабов
Если
требуется исследовать вопрос об угле
или коэффициенте растяжения кривой
![]() при
при
![]() ,
то эту задачу можно решить, рассматривая
кривую
,
то эту задачу можно решить, рассматривая
кривую
 в точке
в точке
![]() .
При решении задач об изменении углов и
масштабов в
при
отображении
можно
руководствоваться следующей таблицей
.
При решении задач об изменении углов и
масштабов в
при
отображении
можно
руководствоваться следующей таблицей
Решение задач с преобразованием углов и масштабов при отображении w=f(z) |
|
Задача |
Решение |
1.
|
См.
|
2.
|
См.
|
3.
|
См.
|
4.
|
См.
|
Пример
1. Исследовать на конформность функцию
![]() в
расширенной комплексной области.
в
расширенной комплексной области.
Решение. В точках отличных от i и конформность следует из существования производной и не равенства её нулю
 .
.
В точке
z=i
значение функции w=,
поэтому для исследования в этой точке
нужно рассмотреть функцию
![]() в точке z=i,
(см. таблицу п. 3 ). Конформность следует
из существования производной и не
равенства её нулю при
в точке z=i,
(см. таблицу п. 3 ). Конформность следует
из существования производной и не
равенства её нулю при
![]() ,
,
 .
.
В точке
z=
значение
функции w=1,
поэтому для исследования на конформность
в этой точке следует «бесконечность в
аргументе» перевести предварительно
в 0
( с помощью замены переменного
![]() ).
Таким образом, для исследования берётся
функция
).
Таким образом, для исследования берётся
функция
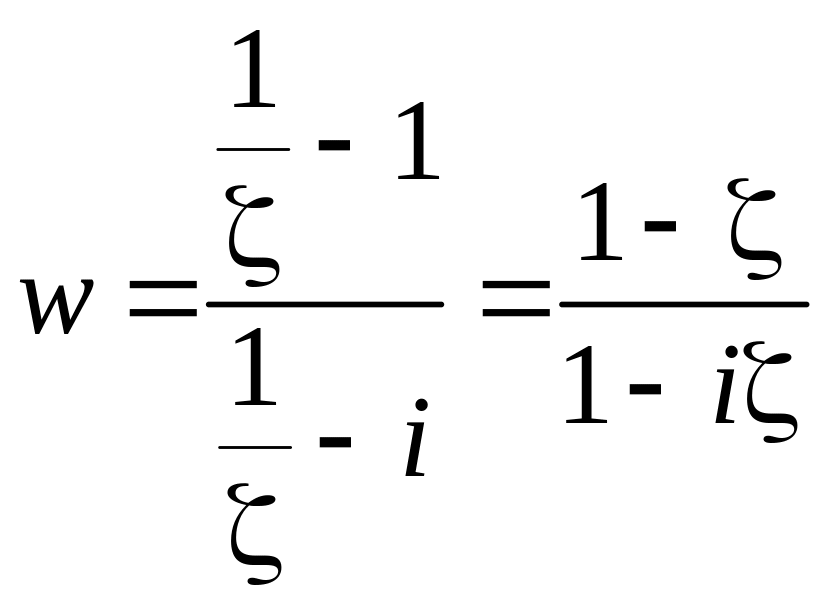 в точке 0,
которая в этой точке имеет производную,
отличную от нуля,
в точке 0,
которая в этой точке имеет производную,
отличную от нуля,
 .
.
Пример 2. Исследовать на конформность в точке z= функцию w=i z - 2.
Решение.
Во всех точках z
производная существует и не равна нулю.
При z=
, w=,
поэтому, согласно определению, необходимо
сделать две замены:
,
и
![]() .
В итоге, для исследования на конформность
имеем функцию
.
В итоге, для исследования на конформность
имеем функцию
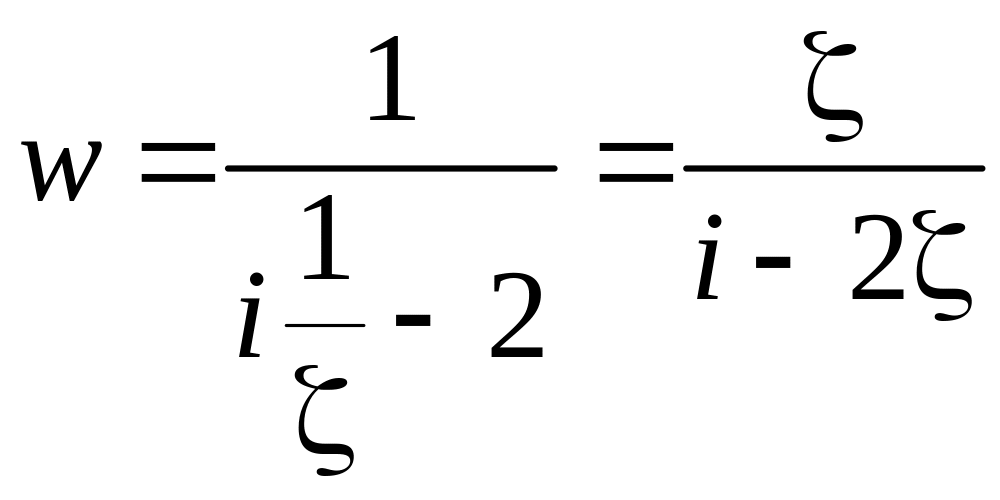 в
окрестности точки
в
окрестности точки
![]() .
Эта функция в точке
имеет производную не равную нулю,
.
Эта функция в точке
имеет производную не равную нулю,
 .
.
Пример
3: Докажем непосредственно свойство
сохранения углов в т. 2i
при отображении
![]() .
.
Пусть
![]() и
и
![]() выходят из точки 2i.
Для первой кривой
выходят из точки 2i.
Для первой кривой
![]() ,
для второй
,
для второй
![]() .
Кроме того
.
Кроме того
![]() Точка 2i
переходит в бесконечность, поэтому
будем искать углы между кривыми
Точка 2i
переходит в бесконечность, поэтому
будем искать углы между кривыми
 и
и
 в
точках
в
точках
![]() ,
соответственно. Для этих кривых имеем
,
соответственно. Для этих кривых имеем
 ,
поэтому угол между образами wk
в бесконечности будет равен:
,
поэтому угол между образами wk
в бесконечности будет равен:

Некоторые свойства конформных отображений ( без доказательства )
Свойство сохранения области. Если f(z) аналитична и однолистна (взаимнооднозначна) в области D, то f(z)0 в D и f(z) конформно отображает D на D* . Кроме того, f -1(w) аналитична в D*, где D* образ D при отображении f(z).
Свойство
сохранения границ.
Пусть D
и D*
две области, ограниченные замкнутыми
кривыми Жордана
и
![]() .
Если f(z)
отображает D
на D*
конформно, то она отображает
.
Если f(z)
отображает D
на D*
конформно, то она отображает
![]() на
на
![]() взаимнооднозначно и взаимно непрерывно
с сохранением направления обхода
границы.
взаимнооднозначно и взаимно непрерывно
с сохранением направления обхода
границы.
Свойство взаимнооднозначного соответствия. Пусть D и D* две односвязные области, ограниченные замкнутыми кусочно-гладкими кривыми Жордана и . Если аналитическая в D функция взаимнооднозначно и непрерывно отображает на с сохранением обхода, то эта функция конформно отображает D на D*.
Теорема ( Риман ). Если граница односвязной области состоит более, чем из одной точки, то существует аналитическая функция, конформно отображающая D на внутренность круга |z|<1, причём эта функция единственна, если задать условия нормировки ( например, перевести заданную точку z0 с заданным направление в заданную точку w0 с заданным направлением.

 в точке w0
0
в точке w0
0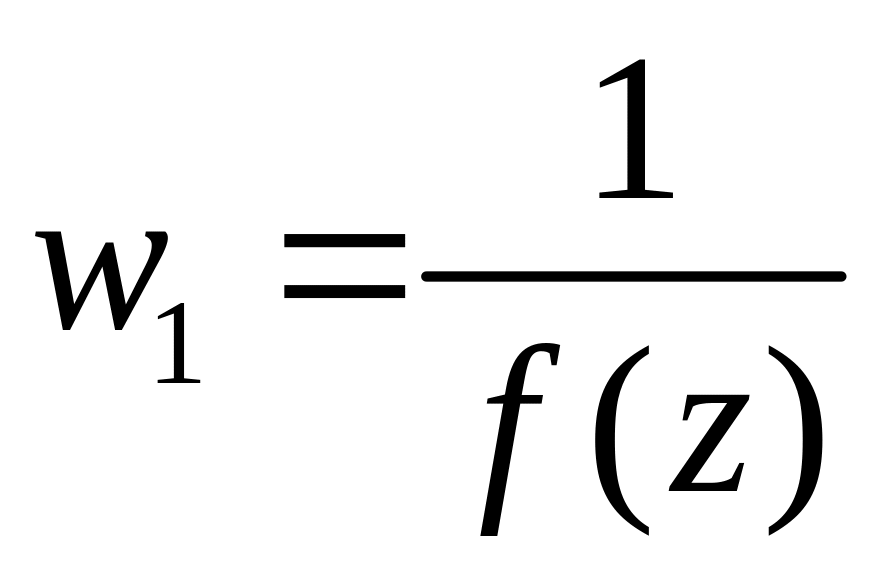 в точке z0
в точке z0 в точке w0
0
в точке w0
0