§2. Вычисление интегралов

1.Определение несобственного интеграла

Особенности на концах. - кусочно-гладкая, ( начало ), (конец ). F(z) непрерывна во всех конечных z на кроме быть может точек a, b. Будем предполагать, что любая окружность с центром в a пересекает кривую не более чем в одной точке.

Рис. 6.3.

Несобственный интеграл определяется по формуле:

.

Определение. Интеграл сходится абсолютно, если существует .

Аналогично определяется несобственный интеграл в случае внутренних особенностей

Рис. 6.4.

.

2. Интегралы вида

Лемма. Если аналитична в , кроме конечного числа особых точек и , то

Рис. 6.5.

Доказательство. Для R>0 рассмотрим контур – верхняя полуокружность, проходимая против часовой стрелки, [-R,R] – отрезок, проходимый слева направо. Считаем, что R выбрано достаточно большим так, что контур C содержит все a_k . Тогда

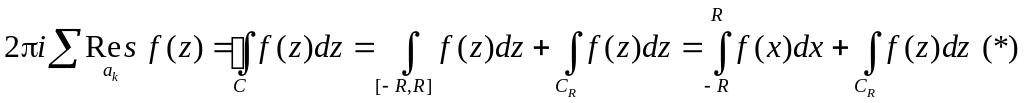
Далее

.

Переходя к пределу в (*) при получим требуемое равенство.

Обобщённая лемма (без доказательства). Если f(z) аналитична в кроме конечного числа особых точек , и конечного числа полюсов первого порядка и , то

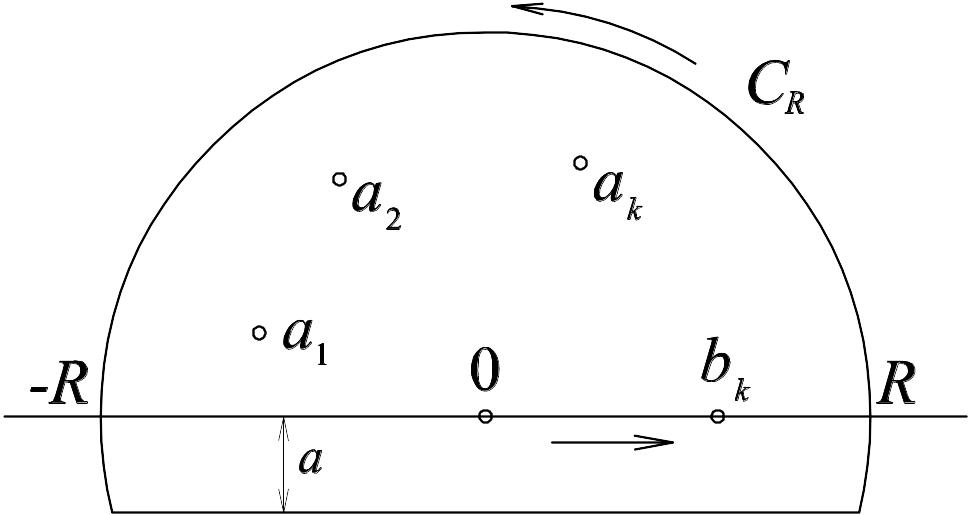
Рис. 6.6.

Пример 1. Вычислить интеграл

.

Пример 2. Вычислить интеграл .

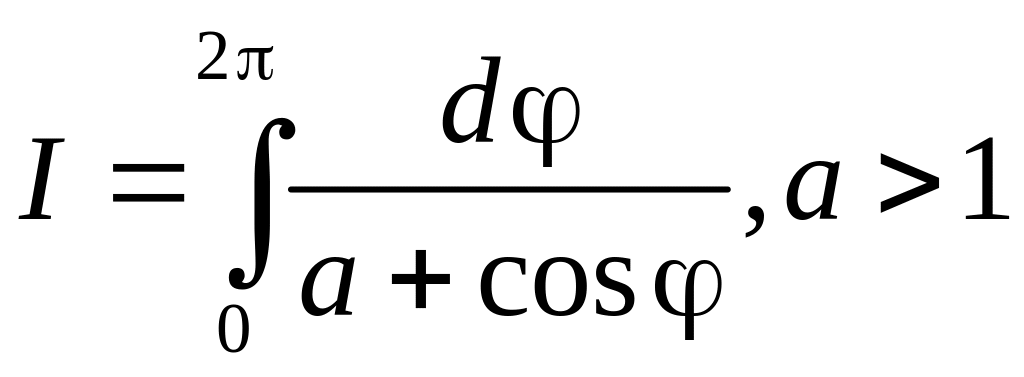, где С – единичная окружность. Корни знаменателя: . Внутри С расположен только один корень . Поэтому .

Пример 3. Вычислить интеграл .

3. Интегралы вида

Лемма Жордана. Если f(z) аналитична в и (C_R - верхняя полуокружность).

Рис. 6.7.

Тогда для любого .

Доказательство. На окружности радиуса R имеем . Тогда, учитывая неравенство , для окружности получим

Следствие. Если f(z) аналитична в кроме конечного числа особых точек , и конечного числа полюсов первого порядка и , то

Пример. Вычислить интеграл .

§3 Простейшие классы аналитических функций.

Определение 1. Однозначная функция f(z) называется целой, если она аналитична в С. Целая функция называется целой рациональной, если её полюс. Целая функция называется целой трансцендентной, если  существенно особая точка.

Примеры. Классифицировать функции .

Свойства целых функций

1. Если устранимая изолированная особая точка целой функции f, то f есть константа.

Доказательство. Существует предел в бесконечности, поэтому f(z) ограничена в окрестности бесконечности, поэтому она постоянна по теореме Лиувилля.

2. Если полюс кратности n (n - натуральное), то f есть полином степени n.

Доказательство.

, обозначим

,

Функция будет, как разность двух целых функций, аналитической во всей комплексной плоскости и имеет в  устранимую особенность, следовательно, она константа по теореме Лиувилля.

Определение 2. Однозначная функция f мероморфна в С, если в любом круге нет других особых точек, кроме полюсов.

Теорема. Если - полюс для мероморфной функции , то она рациональна.

Доказательство. Так как изолированная особая точка, то в расширенной комплексной плоскости имеется лишь конечное число полюсов . Выпишем разложения в ряд Лорана в окрестности каждой из конечных точек :

.

Разложение в окрестности имеет вид:

Функции – рациональные.

имеет точки своими устранимыми особыми точками, поэтому эта функция, после доопределения по непрерывности, будет ограниченной в С и следовательно константой.

Следствие. Рациональная функция представима в виде суммы многочлена и простейших дробей вида . Это фактически доказано в предыдущей теореме.