
- •12. Симметричный четырехполюсник, канонические неуравновешенные и уравновешенные схемы.
- •15. Характеристические (вторичные) параметры пассивных четырехполюсников. Повторное сопротивление четырехполюсника.
- •18. Активные автономные четырехполюсники.
- •47. Методы расчета нелинейных цепей. Графический метод расчета параллельного соединения нелинейных элементов.
- •Типы задач по тоэ
47. Методы расчета нелинейных цепей. Графический метод расчета параллельного соединения нелинейных элементов.
Законы
Кирхгофа:
![]()
Выполняется и для нелинейных цепей, поэтому все методы, основанные на законе Кирхгофа (узловых потенциалов, контурных токов) применимы для расчета нелинейных цепей.
Методы,
основанные на пропорциональности
напряжения току (закон Ома) и принципе
суперпозиции (метод наложения и принцип
взаимности) не применимы. Для нелинейных
цепей метод эквивалентного генератора
формулируется так: любая резистивная
нелинейная активная цепь, рассматриваемая
относительно двух выводов, может быть
заменена источником ЭДС, равным напряжению
между выводами в режиме холостого хода
с последовательно включенным пассивным
нелинейным двухполюсником.
![]()
48. Графический метод расчета последовательного соединений нелинейных элементов.
Последовательное
соединение![]()
![]() ,
НР - нелинейный резистор
,
НР - нелинейный резистор
Метод построения суммарной ВАХ:
![]()

![]()
Параллельное
соединение![]()
По
первому закону Кирхгофа:
![]()
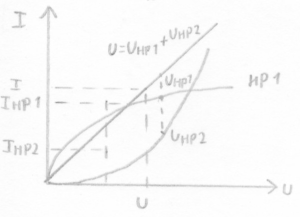
![]()
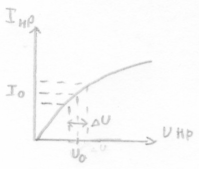
Для характеристики нелинейного резистора необходимо 2 сопротивления (статичное и динамичное - дифференциальное)
![]() -
действующее (амплитудное) значение
-
действующее (амплитудное) значение
![]() переменное
значение
переменное
значение
49. Магнитные цепи. Законы Кирхгофа.
Магнитная цепь - совокупность катушки с током, ферромагнитных тел или каких-либо иных тел или сред, по которым замыкается магнитный поток.
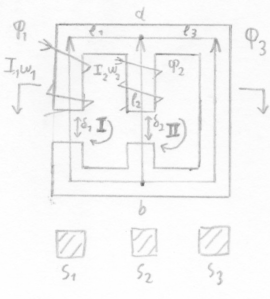
1 Закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю.
![]() . (следует из принципа
непрерывности магнитного потока )
. (следует из принципа
непрерывности магнитного потока )
![]() ,
,![]() -магнитная
индукция, [Тл].1 Тл =
-магнитная
индукция, [Тл].1 Тл =![]() Гс
(Гаусс).
Гс
(Гаусс).![]() напряженность
магнитного поля.
напряженность
магнитного поля.
![]() -магнитная
постоянная;
-магнитная
постоянная;![]() -
относительная магнитная проницаемость
для воздуха или вакуума,
-
относительная магнитная проницаемость
для воздуха или вакуума,![]() для
ферромагнетиков
для
ферромагнетиков
2 Закон Кирхгофа: алгебраическая сумма падений магнитных напряжений вдоль любого замкнутого контура равно алгебраической сумме магнитодвижущих сил (МДС) вдоль того же контура.
![]() (вытекает
из закона полного тока
(вытекает
из закона полного тока![]() )
)
МДС
- произведение числа витков катушки на
протекающий по ней ток. Положительное
направление МДС совпадает с движением
острия правого винта (правило буравчика
или левой руки). Магнитное напряжение
между точками a b и магнитной цепи:![]() ;
;![]() -вектор
направления. Напряжение равно
-вектор
направления. Напряжение равно
![]() ,
если напряженность магнитного поля
,
если напряженность магнитного поля
![]() и
параллельно l (
и
параллельно l (![]() ).
).
Пример:
1
Закон:
![]()
2
Закон: I
![]()
II
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() -
площадь поперечного сечения. Задача
решается расчетом системы уравнений
относительно Ф.
-
площадь поперечного сечения. Задача
решается расчетом системы уравнений
относительно Ф.
50. Магнитное сопротивление участка цепи. Закон Ома для магнитной цепи.
![]()
![]() -
магнитное сопротивление участка цепи
-
магнитное сопротивление участка цепи
В
общем случае
![]() ,
но, когда магнитная цепь насыщена,
,
но, когда магнитная цепь насыщена,
![]() (магнитный
поток зависит от магнитного напряжения)
(магнитный
поток зависит от магнитного напряжения)
![]() -
вебер-амперная характеристика будет
линейна
-
вебер-амперная характеристика будет
линейна
![]() закон
Ома для магнитной цепи
закон
Ома для магнитной цепи
Типы задач по тоэ
1. Несинусоидальные токи и напряжения
Записать выражения для мгновенных значений напряжения u(t) и тока i(t) и определить активную мощность P и полную мощность S, потребляемую схемой. Несинусоидальные ЭДС и ток источников заданы, R, L, C - заданы.
Виды схем:
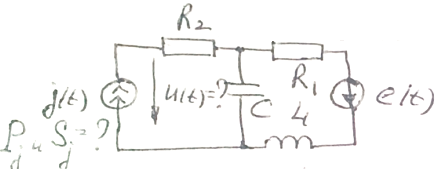
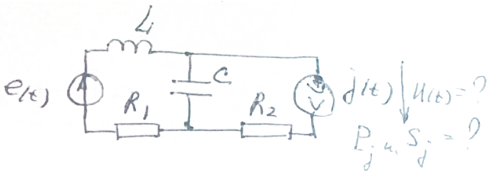
![]()
Формулы:
Активная
мощность
![]()
Полная
мощность![]() ,
,
![]()
Среднее
значение
![]()
Выражение
для мгновенного значения тока![]() ,
,
![]() ,
причем
,
причем![]() ,
,![]() ,
,![]()
Выражение
для мгновенного значения напряжения
![]()
2. Трехфазные цепи
Определить линейные и фазные токи и напряжения, показания ваттметров "звезда" или "треугольник" из цепи.
Виды схем:
![]()
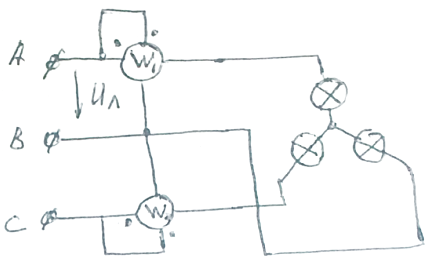
![]()
Заданы
ЭДС генератора, все сопротивления,
номинальная мощность цепи, линейные
напряжения
![]()
Формулы:
Линейный
ток при соединении звездой:
![]()
Линейные
напряжения при соединении звездой равны
разностям фазных напряжений
![]() (1,2
- a, b или с)
(1,2
- a, b или с)
Для
симметричной нагрузки фазный ток при
соединении звездой
![]()
Линейное
напряжение при соединении треугольником![]()
Линейный
ток при соединении треугольником
![]() (1,2
- a, b или с)
(1,2
- a, b или с)
Для
симметричной нагрузки линейный ток при
соединении треугольником![]()
3. Четырехполюсники
Четырехполюсник пассивный симметричный задан канонической схемой. Определить его вторичные параметры: характеристическое сопротивление Zc и гиперболический тангенс постоянной передачи thg.
3. Переходные процессы
Рассчитать классическим методом переходный процесс в цепях первого порядка при постоянном источнике напряжения U или синусоидальном источнике напряжения u(t)=Usin(ωt). Построить графики изменения тока (напряжения), его свободной и принужденной составляющих.
Виды схем:
![]()
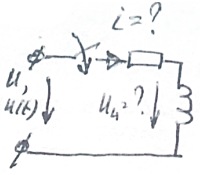
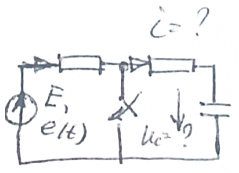
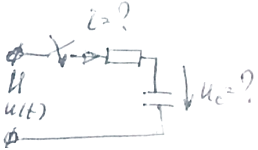
Формулы:
Общая
формула![]()
Принужденная
составляющая![]() (
(![]() )
)
Вычисляем
комплексное сопротивление
![]() (
(![]() )=0
)=0
Записываем
характеристическое уравнение p=(![]() )
)
Свободная
составляющая(![]() ,)
,)
Записываем
ННУ (![]() ,
,
,
,
,
,![]() )
)
Определяем ЗНУ I=A=( )
Пишем решение, подставляя значения
