17. Двумерные фильтрационные течения в прерывно однородных грунтах. Уравнения плоского движения жидкости.

Запишем уравнения плоского движения идеальной несжимаемой жидкости движущейся в потенциальном поле сил. Эти уравнения включают в себя:

- интеграл энергии

- уравнение неразрывности потока

- закон Дарси , , -приведенное давление.

В итоге система из последних трех уравнений позволяет определять четыре неизвестных {ν_x, ν_y, p, ρ}.

Для решения системы уравнений плоского фильтрационного движения жидкости к названным уравнениям необходимо присоединить дополнительное условие отсутствия завихренности потока, которое представлено ниже.

- Условие отсутствия завихренности потока имеет вид

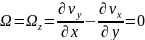
Как известно, из условия отсутствия вихря следует, что дифференциальная форма первого порядка (V^.dr) представляет собой полный дифференциал, т.е справедливо равенство (V^.dr)=dφ. Здесь φ - функция двух переменных (x,y). Поэтому если ввести функцию –которая в гидромеханике называется потенциалом скоростей, такую что выполняется следующие равенства , или , то решение задачи об определении плоского фильтрационного течения можно свести к задаче нахождения функции потенциала скоростей. Таким образом, две независимые функции , переменных (x,y) определяют стационарное поле скоростей фильтрационного течения. функцию тока 

18. Условия Коши-Римана. Двумерное уравнение Лапласа.

Стационарное поле скоростей фильтрационного течения определяют две независимые функции φ,ψ переменных (x,y), где ψ - функция тока и φ- функция потенциала скорости.

Уравнения вида , или , называются условиями Коши-Римана, а явный вид скорости фильтрации через потенциал скорости записан в векторном виде:

Сравнивая это соотношение и формулу закона Дарси выводим важное равенство для дальнейшего изучения плоских фильтрационных потоков

С физической точки зрения это равенство означает, что между потенциалом скоростей и давлением в фильтрационном потоке (с точностью до постоянной интегрирования) имеется прямо пропорциональная зависимость. Согласно общей теории плоского движения жидкости связь между потенциалом скорости φ и функцией тока ψ можно определить также и в виде в виде следующих интегральных соотношений:

, ,

Семейства кривых φ = const называются эквипотенциальными, а семейства кривых ψ = const называются линиями тока. Оба семейства кривых взаимно перпендикулярны, а их условие ортогональности имеет вид .

Если из уравнений , или , исключить либо φ, либо ψ (перекрестным дифференцированием), то находим, что обе эти функции удовлетворяют двумерному уравнению Лапласа.

,

Т. о. задача о плоских, потенциальных течениях идеальной жидкости в установившемся режиме движения сводится к решению уравнения Лапласа при соответствующих граничных условиях, описанных через потенциал скоростей.