
- •1. Основные понятия фильтрации. Основные законы фильтрации. Пористость среды.
- •2. Однородные и неоднородные грунты. Тензор коэффициентов проницаемости грунтов.
- •3.Физическая скорость движения, скорость фильтрации. Уравнение неразрывности.
- •5. Обобщенный закон Дарси для несмешивающихся жидкостей
- •4. Закон Дарси. Эксперимент фильтрации. Границы применимости закона Дарси.
- •6. Общие уравнения фильтрации. Уравнение движения флюида в форме Эйлера
- •7. Закон а. Дарси. Закон Дарси для нестационарных режимов фильтрации
- •8. Обобщенный закон Дарси для анизотропных сред
- •9. Напряженно-деформированное состояние пористой флюидонасыщенной среды. Фильтрация однородного флюида.
- •11. Тензор напряжения в твердом «скелете» горного насыщенного пласта.
- •10. Зависимость параметров флюидов и пористой среды от давления.
- •12. Дифференциальное уравнение неустановившейся фильтрации однородного флюида
- •13. Уравнения установившейся фильтрации несжимаемой жидкости
- •14. Уравнения установившейся фильтрации сжимаемой жидкости. Фильтрация газа
- •15. Простейшие граничные условия, записанные через потенциал скорости
- •20. Уравнение плоского движения фильтрации баротропной жидкости.
- •16. Одномерные фильтрационные потоки в пористой среде
- •17. Двумерные фильтрационные течения в прерывно однородных грунтах. Уравнения плоского движения жидкости.
- •18. Условия Коши-Римана. Двумерное уравнение Лапласа.
- •19. Комплексный потенциал фильтрационного течения. Метод суперпозиции для фильтрационных движений жидкости.
- •21. Фильтрация в однородном грунте
- •22. Фильтрация в искривленных слоях
6. Общие уравнения фильтрации. Уравнение движения флюида в форме Эйлера
Уравнения движения Эйлера является основным и простейшим уравнением динамики идеальной жидкости, которое используется для описания движения фильтрационных потоков флюидов. Векторное уравнение изотермического движения фильтрационного потока можно записать в следующем виде
 через
обозначен
оператор (набла) градиента функции. Это
общее уравнение движения жидкости.
Если фильтрационные движения происходят
с малыми скоростями (так называемые
ползущие
течения (движения) жидкости)
уравнение ползущих течений имеет вид
через
обозначен
оператор (набла) градиента функции. Это
общее уравнение движения жидкости.
Если фильтрационные движения происходят
с малыми скоростями (так называемые
ползущие
течения (движения) жидкости)
уравнение ползущих течений имеет вид
 (2.2) В
случае стационарных (скорость не зависит
от времени) движений формула (2.2) принимает
вид
(2.2) В
случае стационарных (скорость не зависит
от времени) движений формула (2.2) принимает
вид
 .
(2.3)
.
(2.3)
Для
стационарных движений несжимаемой
жидкости происходящих в поле силы
тяжести соотношение (2.3) принимает вид
 (2.4) где
безразмерная величина
(2.4) где
безразмерная величина градиент пьезометрического напора.
Для мелкозернистого грунта и малых
скоростях фильтрации имеет место
зависимость
градиент пьезометрического напора.
Для мелкозернистого грунта и малых
скоростях фильтрации имеет место
зависимость а
в плотных глинах
а
в плотных глинах
 где
где
 -
называется
начальным градиентом.
-
называется
начальным градиентом.
7. Закон а. Дарси. Закон Дарси для нестационарных режимов фильтрации
В
теоретических исследованиях закону
Дарси обычно придают следующую форму
![]()
Приведенное соотношение справедливо только для изотропной среды. Как известно в изотропной среде коэффициенты k и постоянны во всех направлениях движения флюида.
Если
рассматривать фильтрационное течение
в поле силы тяжести и ось z выбрать
вертикально вверх, то дифференциальные
уравнения движения флюида примут вид
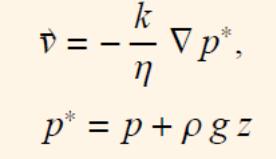
Обращаясь
к равенству
и
заменяя последний член по формуле выводим
следующее уравнение нестационарной
фильтрации в изотропном грунте
выводим
следующее уравнение нестационарной
фильтрации в изотропном грунте
 .
Если
грунт имеет слоистую структуру, то
фильтрация в разных направлениях будет
иметь различные значения коэффициентов
проницаемости.
.
Если
грунт имеет слоистую структуру, то
фильтрация в разных направлениях будет
иметь различные значения коэффициентов
проницаемости.
 ,
(i=1,2,3).
Если
движения происходят настолько медленно,
то членами вида
,
(i=1,2,3).
Если
движения происходят настолько медленно,
то членами вида
 можно
пренебречь, то
можно
пренебречь, то
 ,
(i=1,2,3),
где
vi,
,
p,
Fi
будут
функциями координат и времени.
,
(i=1,2,3),
где
vi,
,
p,
Fi
будут
функциями координат и времени.
8. Обобщенный закон Дарси для анизотропных сред
Анизотропия
означает
неодинаковость физических или
геометрических свойств по различным
направлениям. в реальных коллекторах
анизотропия может быть обусловлена
трещиноватостью, слоистостью. Для
описания постулируется обобщенный
закон Дарси.
 .
.
 компоненты
вектора скорости фильтрации,
компоненты
вектора скорости фильтрации,
 -,
-,
 компоненты
симметричной матрицы (тензора), которая
называется (тензором)
коэффициентов проницаемости.
вид этой матрицы зависит от типа
анизотропии и системы координат, в
которой записан обобщенный закон Дарси.
компоненты
симметричной матрицы (тензора), которая
называется (тензором)
коэффициентов проницаемости.
вид этой матрицы зависит от типа
анизотропии и системы координат, в
которой записан обобщенный закон Дарси.
 ,
,
 ,
,
 ,
Система
координат x1,
y1,
z1,
в которой обобщенный закон Дарси имеет
вид простейший вид, называется главной
системой координат, а значения k1,
k2,
k3
-
главными
значениями тензора проницаемости.
,
Система
координат x1,
y1,
z1,
в которой обобщенный закон Дарси имеет
вид простейший вид, называется главной
системой координат, а значения k1,
k2,
k3
-
главными
значениями тензора проницаемости.
9. Напряженно-деформированное состояние пористой флюидонасыщенной среды. Фильтрация однородного флюида.
Масса
горных пород, расположенных над кровлей
продуктивного пласта, создает так
называемое горное давление
 -
неизменное в процессе разработки
пласта; ρгорн
– средняя плотность горных пород,
слагающих вышележащие пласты, H –
глубина залегания пласта. Предположим,
что кровля и подошва пласта абсолютно
непроницаемы и полностью воспринимают
нагрузку вышележащих пород, тогда
горное давление уравновешивается
напряжением в скелете пласта σ и
давлением p в жидкости:
-
неизменное в процессе разработки
пласта; ρгорн
– средняя плотность горных пород,
слагающих вышележащие пласты, H –
глубина залегания пласта. Предположим,
что кровля и подошва пласта абсолютно
непроницаемы и полностью воспринимают
нагрузку вышележащих пород, тогда
горное давление уравновешивается
напряжением в скелете пласта σ и
давлением p в жидкости:
 ,
σ-
истинное
напряжение в скелете пористой среды,
рассчитанное на единицу горизонтальной
площади, мысленно выделенной в любой
точке пласта; оно действует на части
площади (1 − S).
Поровое давление p действует на остальной
части площади S.
Удобнее ввести эффективное напряжение
σэфф:
,
σ-
истинное
напряжение в скелете пористой среды,
рассчитанное на единицу горизонтальной
площади, мысленно выделенной в любой
точке пласта; оно действует на части
площади (1 − S).
Поровое давление p действует на остальной
части площади S.
Удобнее ввести эффективное напряжение
σэфф:
 .
Тогда
.
Тогда
 .
Эффективное напряжение физически
интерпретируется как часть истинного
напряжения σ в твердой фазе, которая
передается по контакту между зернами
скелета, не зависит от присутствия
жидкости и будет существовать также в
сухой среде. Понятие эффективного
напряжения удобно еще и потому, что его
можно определить из опыта: можно измерить
нагрузку Г, моделирующую горное давление
ρгорн
и поровое давление p,
и найти
.
Эффективное напряжение физически
интерпретируется как часть истинного
напряжения σ в твердой фазе, которая
передается по контакту между зернами
скелета, не зависит от присутствия
жидкости и будет существовать также в
сухой среде. Понятие эффективного
напряжения удобно еще и потому, что его
можно определить из опыта: можно измерить
нагрузку Г, моделирующую горное давление
ρгорн
и поровое давление p,
и найти
 .
При разработке залежи пластовое давление
p падает, и напряжении в скелете σэфф
возрастает.
.
При разработке залежи пластовое давление
p падает, и напряжении в скелете σэфф
возрастает.
