
- •2. Различные способы задания ф-ии нескольких переменных. Линии уровня. Примеры.
- •3. Предел и непрерывность ф-ии нескольких переменных. Св-ва ф-ии непрерывной на замкнутом ограниченном мн-ве.
- •4. Частные производные ф-ии нескольких переменных.
- •5. Дифференциал ф-ии в точке. Дифференциал, как линейная и главная часть приращения ф-ии. Св-ва дифференциала.
- •6.Производная сл.И неявной фy-ии. Инвариантность 1ого дифференциала.
- •7. Производ-я по направлен. Градиент св-ва.
- •8. Производные и диф.Высшего порядков. Независимоть чатсных проиводных от порядка диф-я.
- •11.Необходимые условия экстремума ф-ии нескольких переменных.
- •16.Интегрирование простейших рациональных дробей.
- •18. Инетегрир.Тригонометр.Выраж. И иррациональн.Выраж.
- •19 Опред опред интеграла.
- •21 Производная опред интегр по верх преде.
- •22 Замена переменной в опред интегр.
- •23 Приложен опред интегр. Нахожд V тела.
- •25.Несобственные интегралы
- •2 7.Геометр.Приложения двойных и их вычисление повторным интегрированием
2 7.Геометр.Приложения двойных и их вычисление повторным интегрированием
-поверхность;
 -интегр.сумма;
-интегр.сумма;
![]()
![]() Si=
Vi-объем
параллелепипеда с площ.основания
Si
и высотой
Si=
Vi-объем
параллелепипеда с площ.основания
Si
и высотой
![]() - предел
инт.суммы может интерпретир.как
Vтела.
Геом.смысл
дв.инт.-это
V
тела,ограниченного поверх-тью,
фигурой
D
и некот.цилиндрической поверх-тью по
бокам.
- предел
инт.суммы может интерпретир.как
Vтела.
Геом.смысл
дв.инт.-это
V
тела,ограниченного поверх-тью,
фигурой
D
и некот.цилиндрической поверх-тью по
бокам.
![]() =
=![]() ;
D
проектируется на ось OX.Для
кажд.Х можно говорить о сечении.
;
D
проектируется на ось OX.Для
кажд.Х можно говорить о сечении.
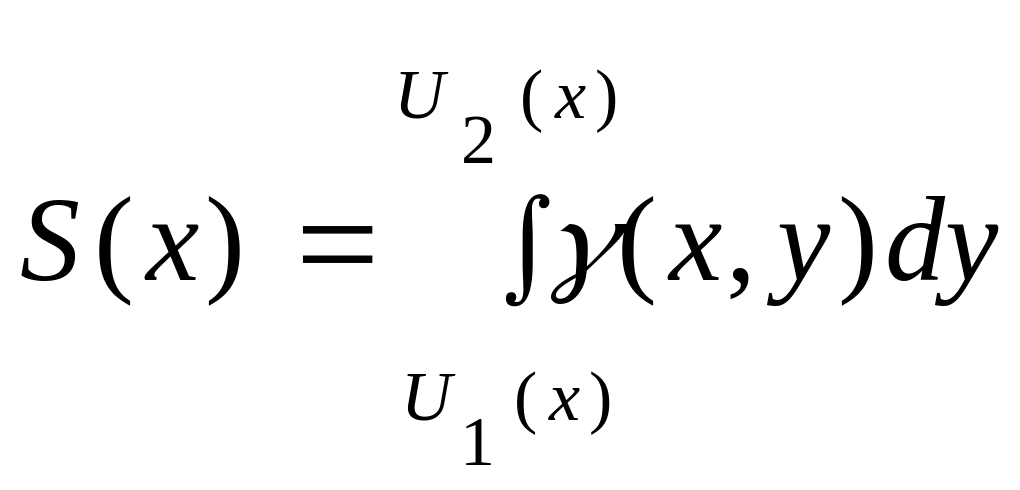
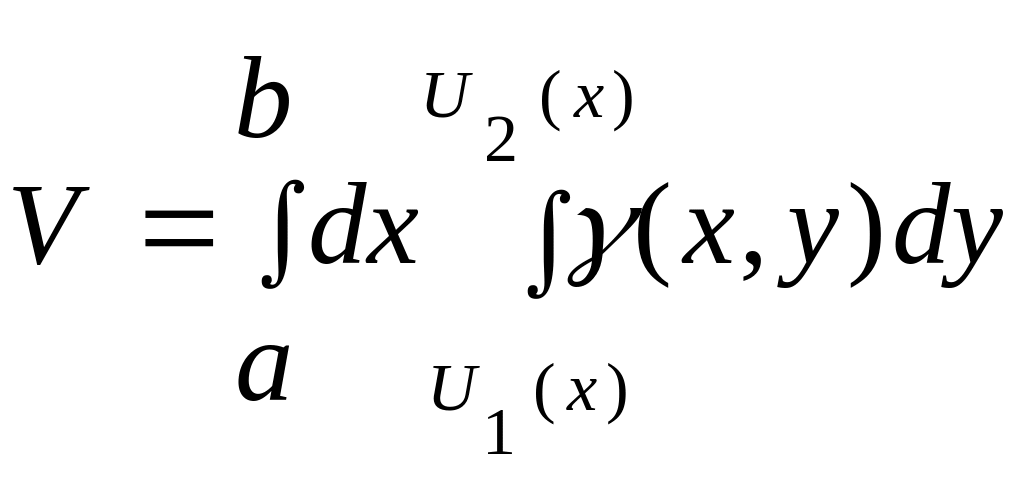 -
это формула повторного интегрирования.
-
это формула повторного интегрирования.![]()
28. ДУ 1 порядка. Общ и час реш. Зад. Коши. Т-ма сущ и ед реш. З-чи, привод к реш ДУ. ДУ – Ур-ия, содерж независ переменную, ф-ю от этой переменной и её производные до n порядка включ.: (1) F(x,y,y’,…y(n))=0 Число n (max порядок производ) наз-ся порядком ДУ. Частным решением ДУ (1) наз. ф-ия, при подстав кот. ур-ие превращ в тождество.Мн-во всех част.решений. наз-ют общим реш. ДУ ДУ (2) y(n)=f(x,y,y’…y(n-1)) наз-ся разрешенным относит-но старшей производной. Задача нахожд реш-й Д У наз-ся интегрирированием Д У. F (x,y,y’)=0; (2) y’=f(x;y)-разреш.отн-но производной (3)P(x,y)dx+Q(x,y)dy=0-симметрич.форма записи ДУ y’=dy/dx; dy/dx=f(x,y); dy=f(x,y)dx; f(x,y)dx-dy=0. В ур-ии (3) можно искать ф-ю y(x) или x(y). Рассм (2) ур-е: касательная в точке tgα=f(x,y’)
Задача Коши: y’=f(x,y); (4) y|x=x0=y0. Найти част.реш-я ур-ия,удовл начал усл-ям, т е знач-я ф-ии при x=x0 равно y=y0. Теор. сущ-я: пусть ф-я f(x,y), f ‘y(x,y) – непр в некот.окрес-ти (.)U(x0,y0)=U(Mo), тогда сущ-ет такая окрест U(x0) и ф-ция y=y(x), заданная в этой окрест-ти,такие, что ф-ция y(x) явл реш з-чи (4),т.е. y(x0)=y0; y(x) удоветв. y’=f(x,y) в окрест-ти точки M0. Такая ф-ия y(x) сущ-ет только одна.
Обл.D непрерывности ф-ции,f’y-непр. Есть точка M0 из обл.D. y’=ky; f(x,y) =ky; f’y=k. Обе ф-ции непрер.на всей пл-ти,и знач.,решением будет y=cekt; y|x=0 =с M(0,c) и оно будет ед реш, проход. через (.) М(0;с)
2![]() 9.
ДУ
с разделяющ и разделён перем-ми.
(*)P(x)dx+Q(y)dy=0
– ДУ с разделенными
пер-ми.
y=y(x)=>
Q(y)dy=Q(y)y’(x)dx;
∫P(x)dx+∫Q(y)y’(x)dx=C;
∫P(x)dx+∫Q(y)y’(x)dx=C;
∫P(x)dx+∫Q(y)dy=C
–это общее реш.(общ.интеграл
ДУ)
(**)m1(x)n1(y)dx+m2(x)n2(y)dy=0
– ДУ с
разделяющ пер-ми.
(m1(x)/m2(x))dx+(n1(y)/n2(y))dy=0
– ДУ с
разделён пер-ми.
–
общий интеграл.
9.
ДУ
с разделяющ и разделён перем-ми.
(*)P(x)dx+Q(y)dy=0
– ДУ с разделенными
пер-ми.
y=y(x)=>
Q(y)dy=Q(y)y’(x)dx;
∫P(x)dx+∫Q(y)y’(x)dx=C;
∫P(x)dx+∫Q(y)y’(x)dx=C;
∫P(x)dx+∫Q(y)dy=C
–это общее реш.(общ.интеграл
ДУ)
(**)m1(x)n1(y)dx+m2(x)n2(y)dy=0
– ДУ с
разделяющ пер-ми.
(m1(x)/m2(x))dx+(n1(y)/n2(y))dy=0
– ДУ с
разделён пер-ми.
–
общий интеграл.
30.
ЛДУ
1 порядка.
ЛДУ 1 п-ка – ур-ия вида y’+p(x)y=q(x).
Реш-е:
будем искать реш как произвед 2
ф-ций:
y=u(x)*v(x);
y’=u’v+uv’
; u’v+uv’+puv=q;
(u’+pu)v+uv’=q(*);
усл-е: u’+pu=0;
(u’)=du/dx=-pu;
du=-pudx;
du/u=-pdx.
Проинтегрируем
по х:
![]()
![]() =-∫p(x)dx;
u=e-∫p(x)dx;
e-∫p(x)dxv’=q(x)
=-∫p(x)dx;
u=e-∫p(x)dx;
e-∫p(x)dxv’=q(x)
31.
Численное решение дифференциального
уравнения. Метод Эйлера.
Ишем
решение (ДУ) на [x0;
b]
= [a;b]
![]() H=(b-a)/n
; h
– шаговое разделение
H=(b-a)/n
; h
– шаговое разделение
|
x |
y |
a= |
X0 |
Y0 |
|
X1 |
Y1 |
|
... |
… |
b= |
Xn |
Yn |
y’=f(x0;y0)
![]()
y(x+h)=y(x) + h*y(x) (*)(*) исходя из определения производной получаем :у1=y(x0+h)≈y(x0)+h*f(x0;y0);у2=y(x1+h)≈y(x1)+h*f(x1;y1). В ответе имеем таблично заданную функцию которая тем ближе к табличному решению, чем меньше число h. Метод Эйлера. Приближенное решение нашего ДУ. Способ оценивания ошибок 1) max | y(x) – yn (x)| x є [a;b] 2) | ỹ(b) – yn (b)| ỹn(x); ỹ2n(x) | ỹn - ỹ2n|. Если данная величина мала, то полученное решение является «достаточно» точным. Задачи оценки кач-ва намного сложнее, чем нахождение решения.
32.
ДУ высших порядков. Общее и частное
решение. Задача Коши. Теорема существования
и единственности решения.
F(x,
y,
y’…y(n))=0;
y(n)=f(x,
y,
y’…y(n-1)).
Решение: 1) общее y=φ(x,
c1…cn)
мн-во всех решений. 2) частное y=y(x)
ф-ия, при подстан. кот. получ. верное
тождество. Задача Коши
![]() теорема
существования и единственности.
Пусть нам дана задача Коши и пусть ф-ии
f,
f’y…f’y(n-1)
непр. M0
(x0,
y0,
y’0…y0n-1).
Тогда сущ. Ux0
и
ф-ия y=y(x)
определённая в этой окрестности такая
что она явл. Решением задачи Коши. Такая
ф-ия сущ. только одна.
теорема
существования и единственности.
Пусть нам дана задача Коши и пусть ф-ии
f,
f’y…f’y(n-1)
непр. M0
(x0,
y0,
y’0…y0n-1).
Тогда сущ. Ux0
и
ф-ия y=y(x)
определённая в этой окрестности такая
что она явл. Решением задачи Коши. Такая
ф-ия сущ. только одна.
33. Линейный дифференциальный оператор n-го порядка и его свойства. Свойства решений линейного однородного дифференциального уравнения. Линейный диф. оператор
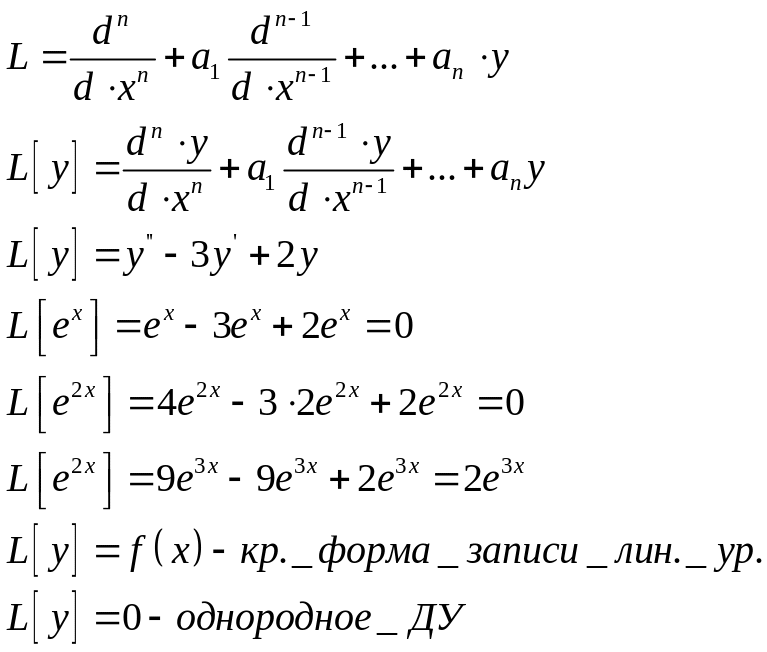
Свойства
![]()
![]()
Доказательство![]()
Исследуем множество решений линейного однородного уравнения, являющегося векторным пространством. Множество функции задано на [a;b] λf(x); f(x)+g(x) ; (f+g)+h=f+(g+h) – ассоц.; f+g=g+f – Коммут.; f+0=f; f+(-f)=0 т.о. мн-во функции является вектором пространства L[y]=0; 1) y - решение=>λy – решение L[λy]= λL[y]=0; 2)y1, y2 – решение; L[y1]= L[y2]=0 => y1 + y2 – решение; L[y1+y2]= L[y1]+ L[y2]=0 На множестве решений можно определить две операции. Множество решений однородного линейного уравнения является векторное пространство
3![]() 4.
Фундаментальная система решений, для
линейного однородного уравнения.
Определитель Вронского.
Фундаментальная
система называется всякий базис множества
y.-
фун-ия линейно независима (y1….yn)-
при добавлении любой другой функции
становится линейно зависима ( для любого
y,
y1…yn,
y
4.
Фундаментальная система решений, для
линейного однородного уравнения.
Определитель Вронского.
Фундаментальная
система называется всякий базис множества
y.-
фун-ия линейно независима (y1….yn)-
при добавлении любой другой функции
становится линейно зависима ( для любого
y,
y1…yn,
y
![]()
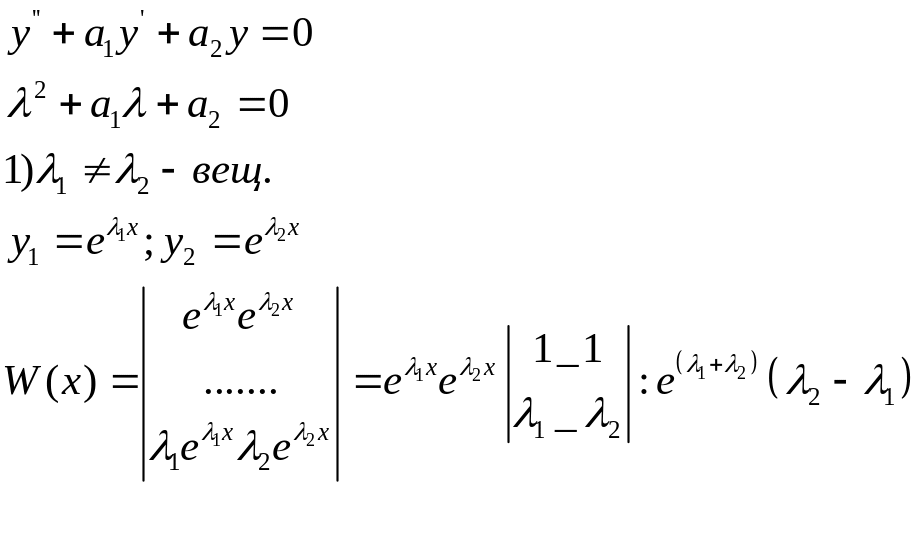 Рассмотрим
ДУ второго порядка
Если λ1≠
λ2
И это вещественное число => W≠0
и => функция y1
и
y2
– линейнонезавис. И сост. Фунд. Сист.
Реш.
Y=c1y1+c2y2
=c1eλ1+c2
eλ2
Рассмотрим
ДУ второго порядка
Если λ1≠
λ2
И это вещественное число => W≠0
и => функция y1
и
y2
– линейнонезавис. И сост. Фунд. Сист.
Реш.
Y=c1y1+c2y2
=c1eλ1+c2
eλ2
Дадим определение определителя Вронского Т1: если y1, y2… yn лин. зависимы, то W(x)=0 для xєX. мн-во – это интервал опред. коэф. ур-я L[y]=0. Т2: если W(x0)=0, то W(x)=0 для всех xєX:u y1, y2… yn – лин. завис. Т3: если W(x0) ≠0, то W(x) ≠0 при любом x єX. W(x0)=0 => по Т.2 W(x)=0 при любом xєX. Т4: Для ДУ сущ. m линейно-независ. ф-ий y1, y2… yn. Нач. ус ловие x=x0. получ. Единичн. Матр. Δ=1=> этим ф-ии лин.независ. Т5: пусть y1, y2… yn. линейно независ. y – произв.
3![]() 5.
теорема о структуре общего решения
линейного неоднородного ДУ n-го
порядка.
Теорема:
общее решение ЛНДУ n-го
порядка равно сумме частного решения
y*
неоднородного
уравнения и общего решения ŷ соответствующего
ему однородного уравнения, т. е. y=y*+
ŷ.
Частное решение y*
ЛНДУ
n-го
порядка может быть найдено, если известно
общее решение ŷ однородного уравнения
, методом вариации произвольных
постоянных. Оно ищется в виде: y*=
c1(x)y1(x)+
c2(x)y2(x)+…+
cn(x)yn(x),
yi(x),
i=от
1 до n-
частные решения, образующие фундаментальную
систему, однородного уравнения.
Система
уравнений для нахождения неизвестных
ci(x)
имеет вид:
5.
теорема о структуре общего решения
линейного неоднородного ДУ n-го
порядка.
Теорема:
общее решение ЛНДУ n-го
порядка равно сумме частного решения
y*
неоднородного
уравнения и общего решения ŷ соответствующего
ему однородного уравнения, т. е. y=y*+
ŷ.
Частное решение y*
ЛНДУ
n-го
порядка может быть найдено, если известно
общее решение ŷ однородного уравнения
, методом вариации произвольных
постоянных. Оно ищется в виде: y*=
c1(x)y1(x)+
c2(x)y2(x)+…+
cn(x)yn(x),
yi(x),
i=от
1 до n-
частные решения, образующие фундаментальную
систему, однородного уравнения.
Система
уравнений для нахождения неизвестных
ci(x)
имеет вид:
Однако для ЛНДУ n-го порядка с пост. коэф., правая часть которого имеет спец. вид, частное решение y* может быть найдено методом неопределённых коэффициентов. Метод подбора частного решения y* уравнения y(n)+p1y(n-1)+…+pny=f(x), где pi – числа, а правая часть f(x) имеет специальный вид.
36.Линейные
ДУ с пост. коэф. И его характеристическое
уравнение. Вид общего решения в случае
различных корней характ. ур-я. ( на примере
ДУ второго порядка)
Частным
случаем однородных ДУ уравнений являются
ЛОДУ с пост. коэф. Пусть дано ЛОДУ второго
порядка: y’’+p•y’+q•y=0;
где p
и q
постоянны. Для нахождения общего решения
уравнения достаточно найти два его
частных решения, образующих фундаментальную
систему. Будем искать частные решения
уравнения в виде y=ekx,
где k-некоторое
число. Дифференцируя эту функцию два
раза и подставляя выражения для y,
y’
и
y’’
в
данное уравнение, получим k2ekx+pkekx+qekx=0,
т.е ekx(k2+pk+q)=0
или k2+pk+q=0
(ekx≠0)-характеристическое
уравнением ДУ. При его решении возможны
следующие три случая. Случай 1: корни k1
и k2
данного
Ур-я действительные и различные:
![]() .
В этом случае частными решениями
уравнения являются функции y1=ek1x
и y2=ek2
x.
Они образуют фундаментальную систему
решений, т. к.
.
В этом случае частными решениями
уравнения являются функции y1=ek1x
и y2=ek2
x.
Они образуют фундаментальную систему
решений, т. к.
![]() .
Следовательно, общее решение уравнения
имеет вид: y=c1ek1x+
c2ek2x.
Билет
37
.
Следовательно, общее решение уравнения
имеет вид: y=c1ek1x+
c2ek2x.
Билет
37
![]() Если
a1…an
– числа, то это ур-е
с постоянными коэфф..
Если
a1…an
– числа, то это ур-е
с постоянными коэфф..
![]()
![]() -
характеристическое
ур-е
y''+a1y'+a2y=0
(диф ур-е 2го порядка),
λ2+a1λ+a2=0,
где
λ1=
λ2
-
характеристическое
ур-е
y''+a1y'+a2y=0
(диф ур-е 2го порядка),
λ2+a1λ+a2=0,
где
λ1=
λ2
![]() a21-4a2=0
λ1=
λ2=
a21-4a2=0
λ1=
λ2=![]() 1
решение: y1=
1
решение: y1=![]() Проверим,
что y2=
Проверим,
что y2=![]() -
тоже решение
y2=
;
y'2=
-
тоже решение
y2=
;
y'2=![]() ;
y''2=
;
y''2=![]() Получим:
Получим:
![]() Учтем,
что λ1=
y2=
-явл
решением, ЧТД
Значит Y=
Учтем,
что λ1=
y2=
-явл
решением, ЧТД
Значит Y=![]() ,
где Y-общ решение
,
где Y-общ решение
Билет
38
Если
a1…an
– числа, то это ур-е
с постоянными коэфф..![]() -
характеристическое
ур-е
y''+a1y'+a2y=0
(диф ур-е 2го порядка),
λ2+a1λ+a2=0,
где λ1,2=α±iβ
y(x)=u(x)+iv(x);
y'(x)=u'(x)+iv'(x)
u(x)-вещ
часть
v(x) – мнимая часть
Теорема.
L[y]=0u(x),
v(x)-решения
L[y]=L[u=iv]=L[u]+iL[v]=0L[u]=L[v]=0
y1,2=
e(α±β)x
-
характеристическое
ур-е
y''+a1y'+a2y=0
(диф ур-е 2го порядка),
λ2+a1λ+a2=0,
где λ1,2=α±iβ
y(x)=u(x)+iv(x);
y'(x)=u'(x)+iv'(x)
u(x)-вещ
часть
v(x) – мнимая часть
Теорема.
L[y]=0u(x),
v(x)-решения
L[y]=L[u=iv]=L[u]+iL[v]=0L[u]=L[v]=0
y1,2=
e(α±β)x
![]()
![]()
![]()
![]() Y=c1eαx·cosβx+c2eαx·sinβx
Y=c1eαx·cosβx+c2eαx·sinβx
Билет
39
Формы
записи: 1) F(x,y,y',…y(n-1))=0
– ДУ n-го порядка;
2) yn=f(x,y,…y(n-1));
3) F(x,y,y')=0;
y'=f(x,y);
4)
![]() 5)
относительно разрешенного
5)
относительно разрешенного
![]() (4)
и (5) – векторная форма записи систем
ДУ
(4)
и (5) – векторная форма записи систем
ДУ
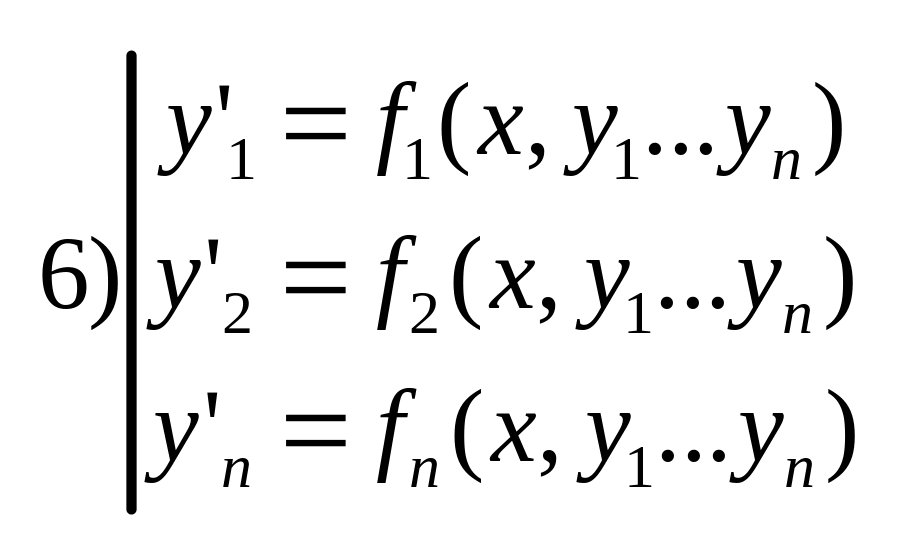 Частное
решение для
(6) - найти упорядоченный набор функций,
при подстановке которых в систему ДУ,
все уравнения обратятся в
тождество.
Частное
решение для
(6) - найти упорядоченный набор функций,
при подстановке которых в систему ДУ,
все уравнения обратятся в
тождество.
![]() (y1(x),…yn(x))
– частное решение
Решить ур-е (5) –
найти вектор-функцию при подстановке
к-рой в ур-ии получилось верное векторное
тождество
Общее
решение-множество
всех решений
7)
(y1(x),…yn(x))
– частное решение
Решить ур-е (5) –
найти вектор-функцию при подстановке
к-рой в ур-ии получилось верное векторное
тождество
Общее
решение-множество
всех решений
7)
![]() Задача
Коши для системы ДУ
Теорема
суш-я
Если фун-я
Задача
Коши для системы ДУ
Теорема
суш-я
Если фун-я
![]() непрерывна
в т. М0(x0,y10,…y10),то
задача Коши (6) имеет единственное решение
у1(x)…yn(x)
в окрестности точки U(x0)
Система
лин. ДУ
Система
линейна, когда ф-я линейна относительно
у1,
y2…yn
(5)-векторная
форма
Y'=AY+B – матричная форма записи
непрерывна
в т. М0(x0,y10,…y10),то
задача Коши (6) имеет единственное решение
у1(x)…yn(x)
в окрестности точки U(x0)
Система
лин. ДУ
Система
линейна, когда ф-я линейна относительно
у1,
y2…yn
(5)-векторная
форма
Y'=AY+B – матричная форма записи
Билет
40.
Yʼ=A*Y
D-множ-во
реш-й сист-ы, элем-ми кот-й явл.матричные
функции.
Т.:множ.D-n
мерное векторное пространство.
Его
базис наз. фунд.сист.реш-й.Все элем-ты
явл. лин.комбин-ми c1Y1+..+cnYn,
где базис Y1..Yn.
Из
опред век.прос-ва:1)если Y1,Y2
–реш-я, тоY1+Y2
тоже реш. 2)если Y
– реш, то cY
тож реш.
Опр-ль Вронского
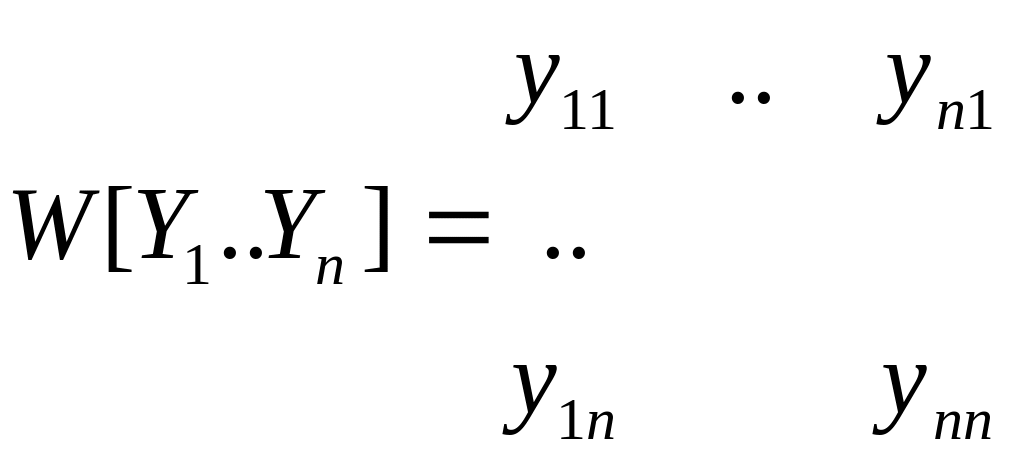 ,
если W=0,
то матрицы Y1..Yn
лин.завис.
Y
имеет вид
,
если W=0,
то матрицы Y1..Yn
лин.завис.
Y
имеет вид
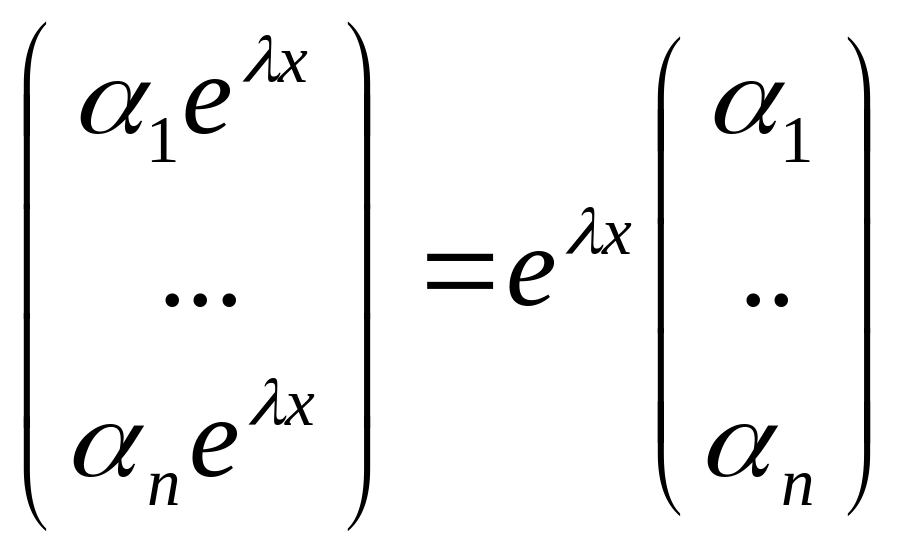 ,
Yʼ=
,
Yʼ=
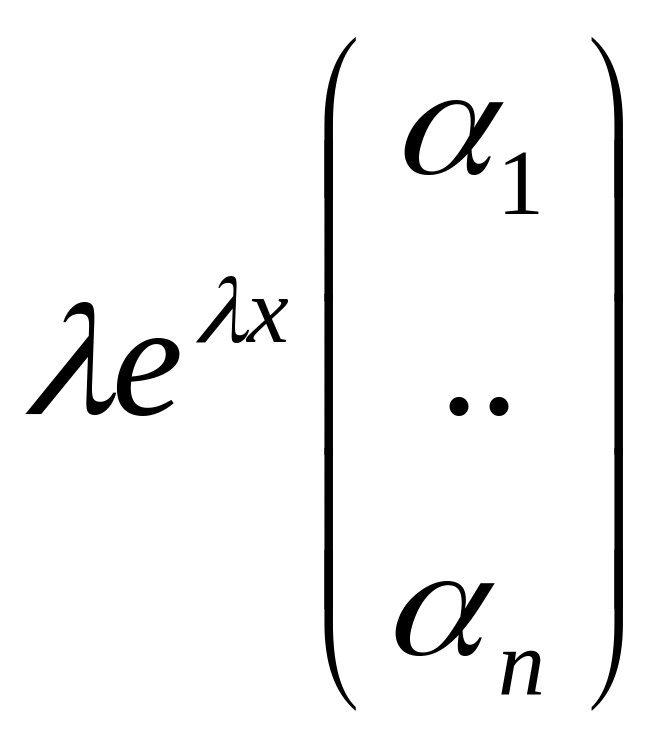 =A*
=A*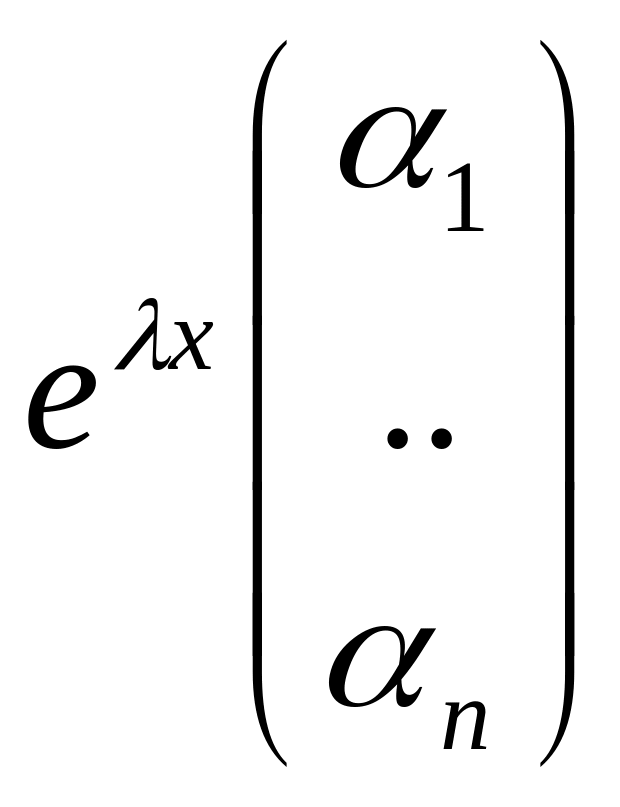 αλ=A*α,
α-соб.вектор
λ-соб.число;
(A-λE)α=0
матрич.форма записи сист., если
А-числа.
det(A-λE)=0
харктеристич.ур.сист., сист. не имеет
реш-й.
Т.:если
корни харак.ур. различны, то базисом
множ. D
будут вектора Yi=eλixαi.
Билет
41.
Дана
an
последовательность, тогда
αλ=A*α,
α-соб.вектор
λ-соб.число;
(A-λE)α=0
матрич.форма записи сист., если
А-числа.
det(A-λE)=0
харктеристич.ур.сист., сист. не имеет
реш-й.
Т.:если
корни харак.ур. различны, то базисом
множ. D
будут вектора Yi=eλixαi.
Билет
41.
Дана
an
последовательность, тогда
![]() =a1+a2+..+an+..
–ряд.
Справа – формальная сумма
бесконечного числа чисел.
частичные
суммы:Sn=a1,..Sn=a1+..+an
Сумма
ряда-предел частичных сумм.
Ряд
сходится, если сущ-ет предел частичных
сумм, в противном случае расходится.
Необход.признак сход-ти: если ряд
сходится, то предел общего члена равен
нулю.
an=Sn-Sn-1
liman=lim(Sn-Sn-1)=limSn-limSn-1=Sn-Sn-1=0.
1+1/2+1/3+..+1/n
–гармонический
ряд.
Задача:исслед.сход-ть
ряда.
Sn=1+1/2+..1/n
>
ln(1+1/1)+ln(1+1/2)+//ln(1+1/n)=ln(2/1+3/2+..(n+1)/n)=ln(n+1).
Sn>ln(n+1)→∞
при
n→∞. Предела
нет,
гарм.
ряд
расход
=a1+a2+..+an+..
–ряд.
Справа – формальная сумма
бесконечного числа чисел.
частичные
суммы:Sn=a1,..Sn=a1+..+an
Сумма
ряда-предел частичных сумм.
Ряд
сходится, если сущ-ет предел частичных
сумм, в противном случае расходится.
Необход.признак сход-ти: если ряд
сходится, то предел общего члена равен
нулю.
an=Sn-Sn-1
liman=lim(Sn-Sn-1)=limSn-limSn-1=Sn-Sn-1=0.
1+1/2+1/3+..+1/n
–гармонический
ряд.
Задача:исслед.сход-ть
ряда.
Sn=1+1/2+..1/n
>
ln(1+1/1)+ln(1+1/2)+//ln(1+1/n)=ln(2/1+3/2+..(n+1)/n)=ln(n+1).
Sn>ln(n+1)→∞
при
n→∞. Предела
нет,
гарм.
ряд
расход
Билет
42.
Геометрич.ряд
-
![]() a+aq+aq2+
..aqn-1..
–сумма членов геомет.прогрессии.
1)при
a=0
S=0
2)Sn=a*(1-qn)/(1-q)
при q≠1.
При
|q|<1
сх. и S=a/(1-q)
При |q|>=1
расх. и предела нет.
Св-ва сход.рядов:
1)если
ряд сх. и его сумма=S,
то λ*ряд тоже сх. и его сумма=λ*S,
т.е. если все члены ряда умножить на
число, то его S
умнож-ся на это число.
a+aq+aq2+
..aqn-1..
–сумма членов геомет.прогрессии.
1)при
a=0
S=0
2)Sn=a*(1-qn)/(1-q)
при q≠1.
При
|q|<1
сх. и S=a/(1-q)
При |q|>=1
расх. и предела нет.
Св-ва сход.рядов:
1)если
ряд сх. и его сумма=S,
то λ*ряд тоже сх. и его сумма=λ*S,
т.е. если все члены ряда умножить на
число, то его S
умнож-ся на это число.
![]() Док-во:
Sn=a1+..+an
λa1+..+λan=λSn
S=limSn
λlimSn=λS.
2)сх.ряды
можно складывать почленно
Док-во:
Sn=a1+..+an
λa1+..+λan=λSn
S=limSn
λlimSn=λS.
2)сх.ряды
можно складывать почленно
![]() 3)если
ряд сх-ся, то сх-ся и ряд, получ-й из
данного отбрасыванием конечного числа
членов. Док-во: a1+..+an+..
ak+1+..+ak+n+..
Sn=a1..+an=Sk+σn-k
σn-k
частич.сумма limSn=lim(Sk+σn-k)=Sk+limσn-k
если сущ. Первый предел, то сущ. и
послед., и наоборот. 4)для
того, чтобы ряд сх-ся, необходимо и
достаточно, чтоб остаток ряда стремился
к нулю. S=a1+..an,
rn=an+1+an+2..,
S=Sn+rn
,
сх.
rn→0.
Док-во:
Sn=S-rn,
S=limSn=lim(S-rn)=S-limrn=0.
3)если
ряд сх-ся, то сх-ся и ряд, получ-й из
данного отбрасыванием конечного числа
членов. Док-во: a1+..+an+..
ak+1+..+ak+n+..
Sn=a1..+an=Sk+σn-k
σn-k
частич.сумма limSn=lim(Sk+σn-k)=Sk+limσn-k
если сущ. Первый предел, то сущ. и
послед., и наоборот. 4)для
того, чтобы ряд сх-ся, необходимо и
достаточно, чтоб остаток ряда стремился
к нулю. S=a1+..an,
rn=an+1+an+2..,
S=Sn+rn
,
сх.
rn→0.
Док-во:
Sn=S-rn,
S=limSn=lim(S-rn)=S-limrn=0.
43.Ряды
с положительными членами. Признак
Даламбера.
Признаки
сходимости:1.признак сравнения(1)
![]() ;
(2)
;
(2)
![]() ;
0≤a
;
0≤a![]() ≤b
-сход.
=>
-сход.
≤b
-сход.
=>
-сход.
-расход.=>
-расход.
Док.-во:
А
=а1+…+аn
(частич сумма 1 ряда)
Bn=b1+…+bn
An≤
Bn,
Аn,
Bn-возрастают
(2)
сход=> Bn
ограничена числом В
В=limBn;
An
≤ В=> An-возрас
и ограничена и знач имеет предел
n->![]() .
Признак Даламбера.
,
an>0,
.
Признак Даламбера.
,
an>0,
![]() =l
=l
![]() l<1
=> ряд сход.
l>1
=> ряд расход (при l=1
приз Далам ответа не дает)
Док-во: 1)
l<1
l<1
=> ряд сход.
l>1
=> ряд расход (при l=1
приз Далам ответа не дает)
Док-во: 1)
l<1
![]() n≤N
n≤N
![]() ≤q<1
a
≤q<1
a![]() ≤q
≤q![]() a
a![]() ≤q
≤q![]() ≤q
≤q![]() an
a
an
a![]() ≤q
≤q![]() *
an
a
*
an
a![]() +a
+…+a
…(*)-сход
по приз срав; остат 1
ряда
a
+a
.q+…+a
.q
+…(**)-геометр
ряд со знач<1=> сход
a
+a
+…+a
…(*)-сход
по приз срав; остат 1
ряда
a
+a
.q+…+a
.q
+…(**)-геометр
ряд со знач<1=> сход
a![]() ≥a
n≥N
если
предел>1, то начиная с некоторого номера
≥1=>
≥a
n≥N
если
предел>1, то начиная с некоторого номера
≥1=>
![]() а
>0=>
ряд расхож по необх признак
а
>0=>
ряд расхож по необх признак
44.Интегральный
признак Коши. Обощенно-гармонический
ряд. Признаки сравнения рядов.
Интегральный
признак Коши
![]() а
Т.:
Пусть
члены ряда убывают и положит., и пусть
ф-я f(n)=an,
тогда ряд an
сход, тогда и только тогда, когда интерг
сход.
Док-во: Sn=a1+a2+…+an
Sn≥
а
Т.:
Пусть
члены ряда убывают и положит., и пусть
ф-я f(n)=an,
тогда ряд an
сход, тогда и только тогда, когда интерг
сход.
Док-во: Sn=a1+a2+…+an
Sn≥![]() f(x)
dx,
a2+a3…+a
<
f(x)
dx
предполож,
что ряд сход., тогда:
≤Sn<S
f(x)
dx≤S=
f(x)
dx,
a2+a3…+a
<
f(x)
dx
предполож,
что ряд сход., тогда:
≤Sn<S
f(x)
dx≤S=![]() f(x)
dx
если
I=
f(x)
сход =>
f(x)
dx<I
S
-a1<I,
знач S
<а1+I
=> огранич и имеет lim,
знач ряд сход.
Обощенно-гармонический
ряд.
Гармонич
ряд наз след ряд: 1+
f(x)
dx
если
I=
f(x)
сход =>
f(x)
dx<I
S
-a1<I,
знач S
<а1+I
=> огранич и имеет lim,
знач ряд сход.
Обощенно-гармонический
ряд.
Гармонич
ряд наз след ряд: 1+![]() -исследов
сход данного ряда:
ln(1+α)>α
e=
(1+
-исследов
сход данного ряда:
ln(1+α)>α
e=
(1+![]() )
)![]() (1+
)
<e
n
ln
(1+
)<1
ln(1+
)<
-запишем
частич
сумму:
Sn=1+
>ln(1+
(1+
)
<e
n
ln
(1+
)<1
ln(1+
)<
-запишем
частич
сумму:
Sn=1+
>ln(1+![]() )+ln(1+
)+ln(1+![]() )+…+ln(1+
)=
ln[
)+…+ln(1+
)=
ln[![]() ]=ln(n+1)
Sn>ln(n+1)
]=ln(n+1)
Sn>ln(n+1)![]() n
гармонич
ряд расход, общий член стремится к
нулю
Признаки
сравнения рядов.
1.признак
сравнения
(1)
;
(2)
;
0≤a
≤b
-сход.
=> -сход.
-расход.=>
-расход.
Док.-во:
А
=а1+…+аn
(частич сумма 1 ряда)
Bn=b1+…+bn
An≤
Bn,
Аn,
Bn-возрастают
(2)
сход=> Bn
ограничена числом В
В=limBn;
An
≤ В=> An-возрас
и ограничена и знач имеет предел
n->
n
гармонич
ряд расход, общий член стремится к
нулю
Признаки
сравнения рядов.
1.признак
сравнения
(1)
;
(2)
;
0≤a
≤b
-сход.
=> -сход.
-расход.=>
-расход.
Док.-во:
А
=а1+…+аn
(частич сумма 1 ряда)
Bn=b1+…+bn
An≤
Bn,
Аn,
Bn-возрастают
(2)
сход=> Bn
ограничена числом В
В=limBn;
An
≤ В=> An-возрас
и ограничена и знач имеет предел
n->
45.
Знакопеременные ряды. Достаточный
признак сходимости. Абсолютная и условная
сходимость.
Знакопеременные
ряды.
(1)
![]() (2)
(2)
![]() если
его члены не имеют произв знач ряд (1)
сход абсолют, если схож ряд (2)
Т.:
Если
ряд (1) сход абсолют, то он сход
Док-во:
Sn=a1+…+an=Sn’-Sn”,
Sn’,Sn”
≥0
Sn’-сумм
положит слаг из 1-х т шт
(-Sn”)-сумм
отриц слаг
если
его члены не имеют произв знач ряд (1)
сход абсолют, если схож ряд (2)
Т.:
Если
ряд (1) сход абсолют, то он сход
Док-во:
Sn=a1+…+an=Sn’-Sn”,
Sn’,Sn”
≥0
Sn’-сумм
положит слаг из 1-х т шт
(-Sn”)-сумм
отриц слаг
![]() -сумм
ряд (2)
-сумм
ряд (2)
![]() =Sn’+Sn”
Если
ряд (2) сход => что
<δ(огранич),
а знач Sn’
и Sn”-огранич
(<
)=>Sn’-S’;
Sn”
=Sn’+Sn”
Если
ряд (2) сход => что
<δ(огранич),
а знач Sn’
и Sn”-огранич
(<
)=>Sn’-S’;
Sn”![]() S”
Sn=
(Sn’-Sn”)=S’-S”
замечания:
сход ряда не след его абсол
при измен
порядка слаг в усл-сход ряду, его сумм
мож изменит, т.е.какое бы ни было S
можно так изменит поряд слаг. в усл-сход
ряду, что его сумм=S
Достаточный
признак сходимости
Если
an
не стремится к нулю, то ряд не может быть
сход-ся, т.е. он расход-ся.
Пример:
S”
Sn=
(Sn’-Sn”)=S’-S”
замечания:
сход ряда не след его абсол
при измен
порядка слаг в усл-сход ряду, его сумм
мож изменит, т.е.какое бы ни было S
можно так изменит поряд слаг. в усл-сход
ряду, что его сумм=S
Достаточный
признак сходимости
Если
an
не стремится к нулю, то ряд не может быть
сход-ся, т.е. он расход-ся.
Пример:
![]() =>
ряд
расход, ибо его общ член an=
=>
ряд
расход, ибо его общ член an=![]() при n
,
стремится к 1/100 и знач не стремит к нулю.
!!!
стремление
n-го
члена ряда к 0 не яв-ся достаточным для
сход ряда!!!
Абсолютная
и условная сходимость.
Есл
ряд, состав из абсолют велич член дан
ряда, сх-ся, то сх-ся и дан ряд
Ряд
наз-ся сход относ(усл), есл он сход, а ряд
из его модул расход.
при n
,
стремится к 1/100 и знач не стремит к нулю.
!!!
стремление
n-го
члена ряда к 0 не яв-ся достаточным для
сход ряда!!!
Абсолютная
и условная сходимость.
Есл
ряд, состав из абсолют велич член дан
ряда, сх-ся, то сх-ся и дан ряд
Ряд
наз-ся сход относ(усл), есл он сход, а ряд
из его модул расход.
46.Теорема
Лейбница
Знакочеред.
ряд
с
убыв
член
сход-ся:
![]() an,
an,
![]() <a1,
an>0
Есл
предел
общ
чл=0
<a1,
an>0
Есл
предел
общ
чл=0
![]() =0
=>
an-ax,
a
>an,
an>0
Док-во
S2n=(a1-a2)+(a5-a4)+…+(a
=0
=>
an-ax,
a
>an,
an>0
Док-во
S2n=(a1-a2)+(a5-a4)+…+(a![]() -a2n);
S2n>0,
S2n-возрас
S2n=a1(a2-a3)-(a4-a5)-…-(a
-a2n);
S2n>0,
S2n-возрас
S2n=a1(a2-a3)-(a4-a5)-…-(a![]() -a
)-a2n
S2n<a1-огранич
=> S2n
S
-a
)-a2n
S2n<a1-огранич
=> S2n
S![]() =S+0
Сл1:
an;
a
<an;
an>0
Sn=S=>
S<ax
Сл2:
|S-Sn|< a
абсолют
ошибка
замены
S на
Sn и
она
<1-го
отбрас
чл
Sn
=S+0
Сл1:
an;
a
<an;
an>0
Sn=S=>
S<ax
Сл2:
|S-Sn|< a
абсолют
ошибка
замены
S на
Sn и
она
<1-го
отбрас
чл
Sn![]() S
S
47.Функциональные ряды. Это ряд вида: U1(x)+U2(x)+…+Un(x)…(1) S1(x)=U1(x); Sn(x)=U1(x)+…+Un(x) S(x)= Sn(x) Обл сход ряд(1)-мн-во Х, для кот ряд(1)сход. Это есть обл опред ф-и f(x)
48.
Степенный ряды.
Степенным
рядом наз-ся функц ряд
(3)a0+a1(x-a)+a2(x-a)
+…+an(x-a)
чл
кот суть произв пост а0,а1,ат на степен
ф-ции с цел показ степен от разнос
х-а
Теорема
Абиля:
(2)а0+а1х+…+аnx+…
а)
есл (2)сход при х0, то он сход при
|x|<|x0|
б)есл
(2) расход при х0, то он расход при
|x|>|x0|
Док-во:
а0+а1х+…+аnx
+…
|a0|+|a1||x|+…+|an||x|
+…=|a0|+|a1x0||![]() |+…+|anx
|+…+|anx![]() 0||
0||![]() |
+…(*)
|
+…(*)
![]() -сход
=>
-сход
=>
![]() =>0=>|
=>0=>|![]() |<M
<M(1+|
|+…+|
|<M
<M(1+|
|+…+|![]() |
-q=|
|
-геомет ряд со знач сход при q=1=>
ряд(*) сход по приз срав с геом ряд; а
первон ряд сход абсол
есл ряд(2) расход
при х’0 и пусть при |x|>|x0|-сход
(х-сх-ся=>
x’0-сход
это противор)
Радиус
и интервал сход-ти степен ряда:
Радиусом
сход-ти степен ряда наз-ся такое число
R,
что для всех x,
|x|<R,
степен ряд сход, я для всех x,
|x|>R,
расход. Интервал (-R,R)-интервал
сход-ти
|
-q=|
|
-геомет ряд со знач сход при q=1=>
ряд(*) сход по приз срав с геом ряд; а
первон ряд сход абсол
есл ряд(2) расход
при х’0 и пусть при |x|>|x0|-сход
(х-сх-ся=>
x’0-сход
это противор)
Радиус
и интервал сход-ти степен ряда:
Радиусом
сход-ти степен ряда наз-ся такое число
R,
что для всех x,
|x|<R,
степен ряд сход, я для всех x,
|x|>R,
расход. Интервал (-R,R)-интервал
сход-ти
