
- •2. Различные способы задания ф-ии нескольких переменных. Линии уровня. Примеры.
- •3. Предел и непрерывность ф-ии нескольких переменных. Св-ва ф-ии непрерывной на замкнутом ограниченном мн-ве.
- •4. Частные производные ф-ии нескольких переменных.
- •5. Дифференциал ф-ии в точке. Дифференциал, как линейная и главная часть приращения ф-ии. Св-ва дифференциала.
- •6.Производная сл.И неявной фy-ии. Инвариантность 1ого дифференциала.
- •7. Производ-я по направлен. Градиент св-ва.
- •8. Производные и диф.Высшего порядков. Независимоть чатсных проиводных от порядка диф-я.
- •11.Необходимые условия экстремума ф-ии нескольких переменных.
- •16.Интегрирование простейших рациональных дробей.
- •18. Инетегрир.Тригонометр.Выраж. И иррациональн.Выраж.
- •19 Опред опред интеграла.
- •21 Производная опред интегр по верх преде.
- •22 Замена переменной в опред интегр.
- •23 Приложен опред интегр. Нахожд V тела.
- •25.Несобственные интегралы
- •2 7.Геометр.Приложения двойных и их вычисление повторным интегрированием
22 Замена переменной в опред интегр.
З![]()
![]() амена
переем:
Пусть дана у=в(х) на пром [a,b],
х=(t)
непрер и диффер на [,];
()=a,
()=b
То
Док-во:
амена
переем:
Пусть дана у=в(х) на пром [a,b],
х=(t)
непрер и диффер на [,];
()=a,
()=b
То
Док-во:
![]()
![]()
п![]() о
частям:
о
частям:
Д![]()
![]()
![]() ок-во:
ок-во:
23 Приложен опред интегр. Нахожд V тела.
1![]() )Вычисл
площ Пусть
дана обл, оганич сверху y=f2(x)
и снузу y=f1(x),
x=a,
x=b:
)Вычисл
площ Пусть
дана обл, оганич сверху y=f2(x)
и снузу y=f1(x),
x=a,
x=b:
2![]()
![]() )Выч
объма по S
сечен: a,b-
концы проекц тела на Ох. A=x0x1x2...xn=b.
s(c1),
S(с)
-площ попер сеч. S(c1)x1=V1-объем
цилиндр тела с площ основания S(c1)
и высотой x1.Sn=S(c1)x1+…+S(Cn)
)Xn-объем
составного цилиндрич тела. Объем данного
тела:
)Выч
объма по S
сечен: a,b-
концы проекц тела на Ох. A=x0x1x2...xn=b.
s(c1),
S(с)
-площ попер сеч. S(c1)x1=V1-объем
цилиндр тела с площ основания S(c1)
и высотой x1.Sn=S(c1)x1+…+S(Cn)
)Xn-объем
составного цилиндрич тела. Объем данного
тела:
![]() Так
обр: объем- интеграл от поперечных сечен
Так
обр: объем- интеграл от поперечных сечен
3![]() )V
тела вращ: Криволин
трапец вращается вокруг Оч, получ тело
вращен. Получаемое сечен – круг. r=f(x),
S(x)=f2(x)
)V
тела вращ: Криволин
трапец вращается вокруг Оч, получ тело
вращен. Получаемое сечен – круг. r=f(x),
S(x)=f2(x)
2![]() 4
численные методы интегрирован.
Разоб
отрез а-в на n-равн
част. H=x1-x0=x2-x1=...=(b-a)\n
Yi=f(xi)
Ф-ла
Лев прямоугольников:
4
численные методы интегрирован.
Разоб
отрез а-в на n-равн
част. H=x1-x0=x2-x1=...=(b-a)\n
Yi=f(xi)
Ф-ла
Лев прямоугольников:
Ф![]() -ла
Прав прямоугольников:
-ла
Прав прямоугольников:
П![]() ри
увеличении nточность
формул возрастает.
Ф-ла
трапеций
ри
увеличении nточность
формул возрастает.
Ф-ла
трапеций
![]()
П![]() усть
I-точное
знач инт, In-приближ
знач инт
In-I}=-
абсолютная ошибка
усть
I-точное
знач инт, In-приближ
знач инт
In-I}=-
абсолютная ошибка
Д![]()
![]() ля
трап:
где
ля
трап:
где
Д![]() ля
прямоуг:
где
ля
прямоуг:
где
25.Несобственные интегралы
Это опред.интеграл от непрер.ф-ции,но с бескон.промежутком интегрирования иои опред.интеграл с конеч.промеж.интегрирования,но от ф-ции,имеющей на нем бесконечный разрыв.
1)Интеграл
по неогранич.обл-ти (бескон.промежутку)
![]() - ф-ция
непрер. на [а;
- ф-ция
непрер. на [а;![]() ).Возьмем
на этом промежутке число b.
).Возьмем
на этом промежутке число b.
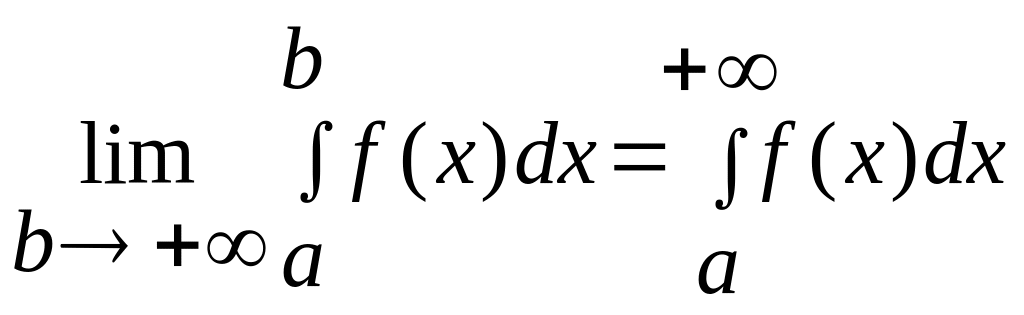 - интегралом от а до
наз-ся lim..,где
верхний предел стремится к бесконечности.
Если предел сущ-ет,интеграл наз-ся
сходящимся, в прот.случае расходящимся.
- интегралом от а до
наз-ся lim..,где
верхний предел стремится к бесконечности.
Если предел сущ-ет,интеграл наз-ся
сходящимся, в прот.случае расходящимся.![]()
![]()
2![]() )
Интегралы по неограниченным областям
)
Интегралы по неограниченным областям
f(x)![]() +
+
![]() ;x
b-0
;x
b-0
![]()
![]() - Выбирая Сn,близкое
к b,знач-е
интегр.суммы будет сколь угодно
большое.Знач.,не будет lim.Выберем
точку C
и рассм.Sn:
- Выбирая Сn,близкое
к b,знач-е
интегр.суммы будет сколь угодно
большое.Знач.,не будет lim.Выберем
точку C
и рассм.Sn:
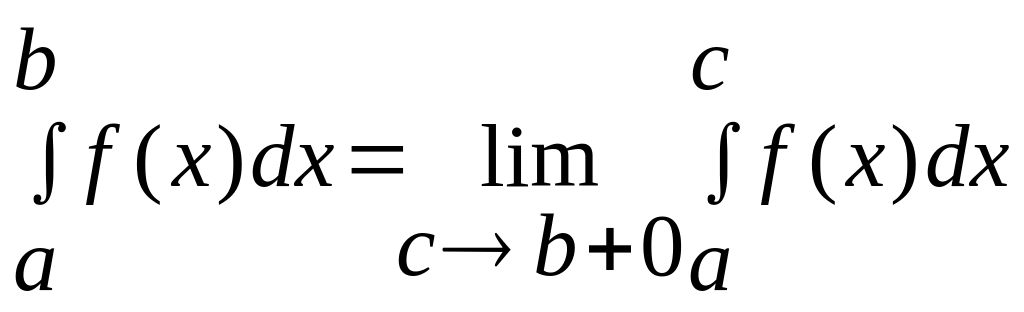 .
Если lim
сущ-ет,то предел наз-ся сходящимся.
.
Если lim
сущ-ет,то предел наз-ся сходящимся.
26.Общая схема построения опред.интеграла.Двойной интеграл и его cв-ва. 1) а) Дана ограниче.обл-ть: y=f2(x) сверху,y=f1(x) cнизу. x=a,x=b. Найти площадь фигуры-это площадь разности 2 площадей.
![]()
![]() б)Вычисление
объема тела по площадям поперечных
сечений.
б)Вычисление
объема тела по площадям поперечных
сечений.
S![]()
![]() (x)-площадь
попереч.сечения пл-ти х. a,b-концы
проекции тела на ОХ. Разобьем [a,b]
на n-частей,в
кажд.части возьмем по точке(с1,с2…сn).
(x)-площадь
попереч.сечения пл-ти х. a,b-концы
проекции тела на ОХ. Разобьем [a,b]
на n-частей,в
кажд.части возьмем по точке(с1,с2…сn).
![]() .
Тогда S(c1)…S(cn)-площади
поперечного сечения в соответ.точках.
S(c1)
.
Тогда S(c1)…S(cn)-площади
поперечного сечения в соответ.точках.
S(c1)![]() x1=
V1-объем
цилиндрического тела с площадью основания
S(c1)
и высотой
х1.
Sn=S(c1)
x1+…+S(cn)
xn-объем
составной цилиндрической фигуры.
x1=
V1-объем
цилиндрического тела с площадью основания
S(c1)
и высотой
х1.
Sn=S(c1)
x1+…+S(cn)
xn-объем
составной цилиндрической фигуры.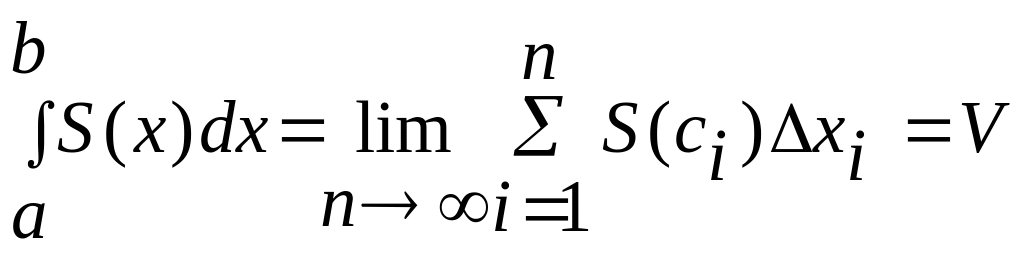
![]() Объем-это интеграл от поперечных
сечений
2) Дана пластина D(обл-ть
на пл-ти).
Объем-это интеграл от поперечных
сечений
2) Дана пластина D(обл-ть
на пл-ти).
![]() -плотность
пластины в точке М.
-плотность
пластины в точке М.
![]() ,
где m-масса
пластины.Найти массу пластины обл-ти
D.
Разобьем пластину линиями,парал.осям
координат.
Di-части;
D1…Dn;
в кажд.части берем по точке.
*
S1
,
где m-масса
пластины.Найти массу пластины обл-ти
D.
Разобьем пластину линиями,парал.осям
координат.
Di-части;
D1…Dn;
в кажд.части берем по точке.
*
S1![]()
![]() m1,
где
S1-площадь
части
m1,
где
S1-площадь
части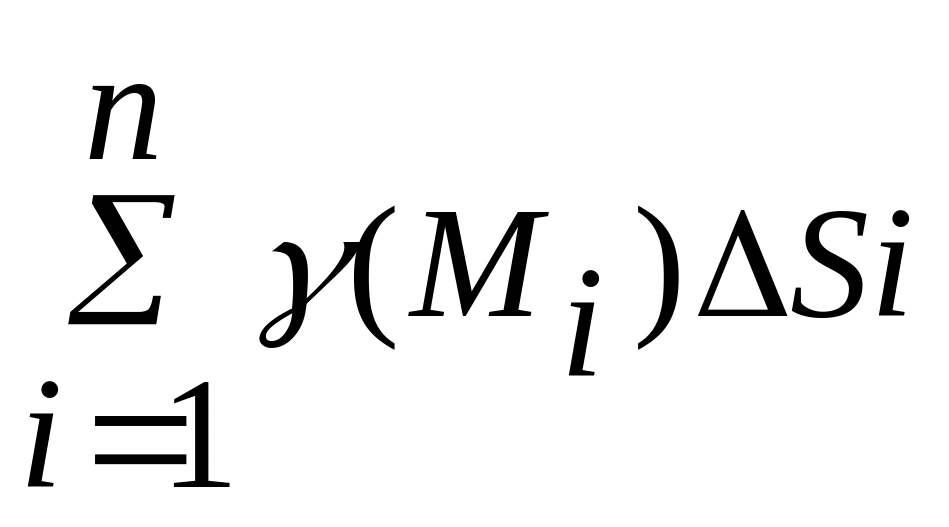 -
приближ.знач-е массы пластины D.
Переходя к пределам,получим точное
знач-е:
-
приближ.знач-е массы пластины D.
Переходя к пределам,получим точное
знач-е:
![]() Двойным
интегралом от
Двойным
интегралом от
![]() dS
наз-ся предел интегр.суммы
Масса
пластины-двойной интеграл от
по
обл-ти D:
dS
наз-ся предел интегр.суммы
Масса
пластины-двойной интеграл от
по
обл-ти D:
![]()
Cв-ва:1.св-во
линейности:
а)![]() -однородность;
б)
-однородность;
б)![]() -адитивность.
Теор.существования
-адитивность.
Теор.существования
![]() :Если
подынтегр.ф-ция непрер.на замкн.огранич.обл-ти
D,то
она интегрируема на этой обл-ти.
2.св-во
адитивности по обл.интегрирования:
Если
:Если
подынтегр.ф-ция непрер.на замкн.огранич.обл-ти
D,то
она интегрируема на этой обл-ти.
2.св-во
адитивности по обл.интегрирования:
Если
![]() ,
то
,
то
![]()
