6.Производная сл.И неявной фy-ии. Инвариантность 1ого дифференциала.

Производ.сл.ф-ии:

Теорем.: если ф-ия z=f(x;y) и ф-ия x=x(t) y=y(t) диффер. В соответствующ. Точках, то производ. dz/dt=dz/∂x*dx/dt=∂z/∂y*dy/dt. Z(t)=f(x(t);y(t)) f: Rⁿ→R F(t)=x(t);y(t) :Rⁿ→R. док-во: ∆z=∂z/∂x*∆x+∂z/∂y*∆y+o(∆ρ) f→(x,y) ∆f→∆x;∆y;∆z. ∆z/t=∂z/∂x*∆x/∆t+∂z/∂y*∆y/∆t+

α это = dz/dt=dx/dt+dy/dt

Производ.неяв.ф-ии:

F(x,y)=0 возьмем число x →поставим в ур-е →решим относительно y →получаем значение–является значением ф-ии в точ. x. Т. о существован.неяв.ф-ии: пусть ф-ия f непрерыв и диффер-ема в окресност. Точ. М₀, т.е. имеет непрерыв.производные F’_x и F’_y и F’_y(M₀)≠0, тогда существует такая окресност.точ.x₀ и ф-ия y=y(x), определен-ая в этой окрестности, которая: 1) y(x₀)=y₀ 2)f(x,y(x))=0 для всех точек этой окрестности 3)y(x) – дифференц-ема в окрест.точ.x₀. если верно равенство 2: f'_x*dx/dx+f’_y*dy/dx=0 dy/dx=-f’_x/f’_y

Инвариантность 1ого дифференциала:

Y=f(x); dy=y’dx; z=f(x,y); dz=z’_xdx+z_ydy – если независим.перемен. пусть x и y –ф-ии от переменных, т.е. x=x(t) y=y(t). dz=z’_tdt=(z’_xx’_t+z’_yy’_t)dt=z’_tx’_tdt+z’_yy’_tdt=z’_xdx+z’_ydy

Формула верна, независимо от того, что чбн независим.переменные или ф-ии от некотор.переменных.

7. Производ-я по направлен. Градиент св-ва.

Скалярное произв-возможн инетрпритации ф-и нескольких переменных(поле, давление и т.д.) U=u(m) U(m)*u(m)= ∆u(приращ); M₀M= ta₀(где_a_0=1); ∆u/_М₀М_- опред.скорость направления L(луча); производ.ф-и по направлен а₀

Физич.смысл:Скорость изменения ф-и в направлен а_0.

u=u(x,y)

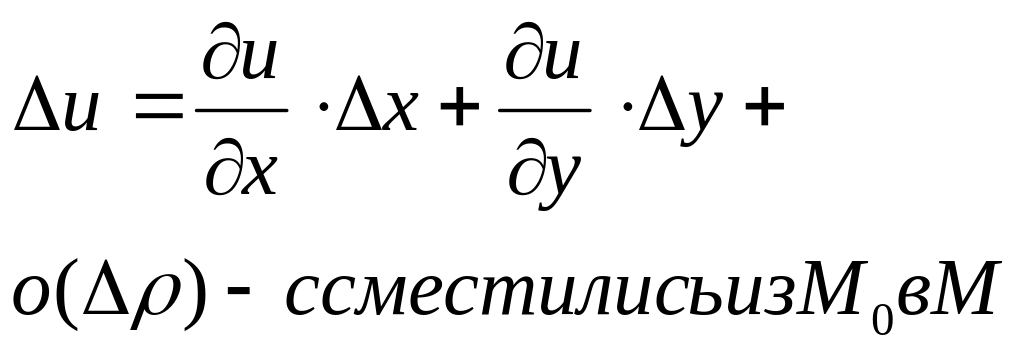
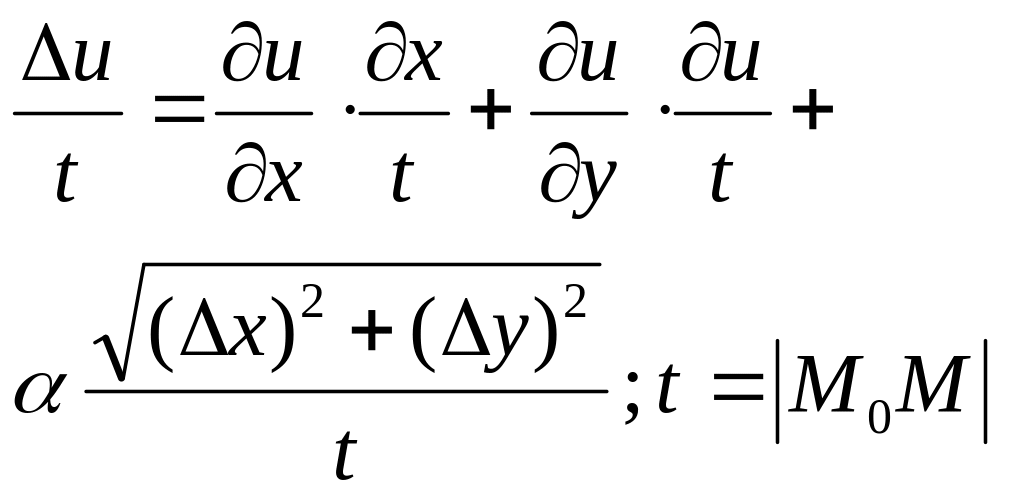
ф-а производ по направ.:

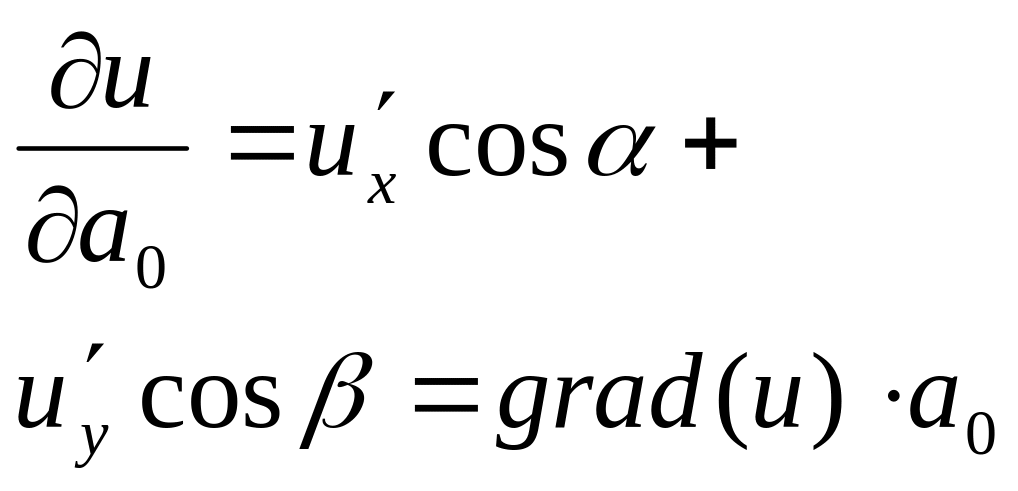
Где grad(u)=(u_x;u_y)-указывает направление наибольшего возрастания ф-и. А₀=(cos;cos) Скалярн произвед вектора градиента на единичный вектор направлении- производная оп направлению. Если а₀ совпадает с grad(u)то производная по напрвлению принимает наибол значение, если а₀grad(u), =0

8. Производные и диф.Высшего порядков. Независимоть чатсных проиводных от порядка диф-я.

Ф-я зависит от (x,y,dx,dy)

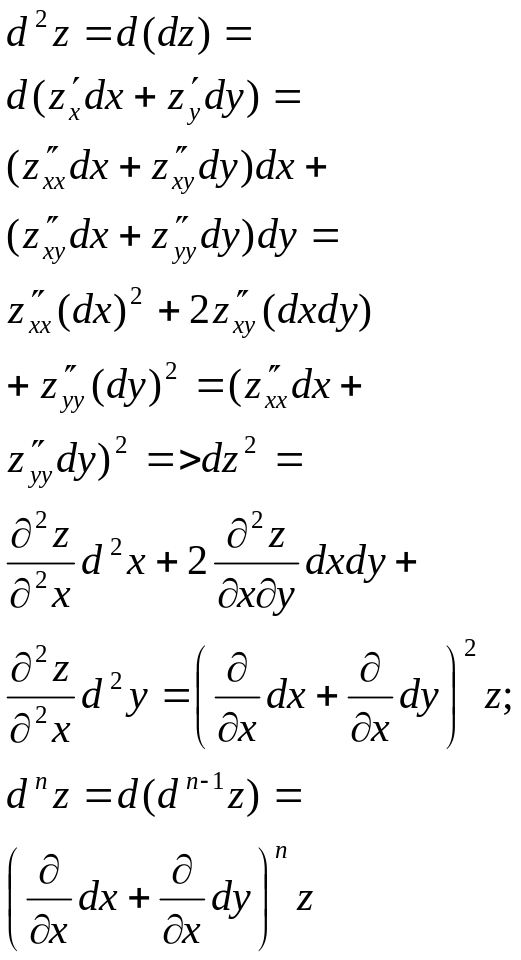формула для n-дифференциала. Частные производные можно дифф.по Х и по Y.если находятся в окрестности M₀ и непрерывны в окрестности M₀; если частная производная Y,т.е значение производной независят от порядка дифф-я, то они РАВНЫ.

Я НЕ СМОГЛА НАЙТИ ПРОИЗВОДНЫЕ ВЫСШЕГО ПОРЯЛКА..=(

9. касательная плоскости и нормаль к поверхности. Z=f(x,y);F(x,y,z)=0

F(x(t):y(t);z(t))=0(при любых t)=>диф: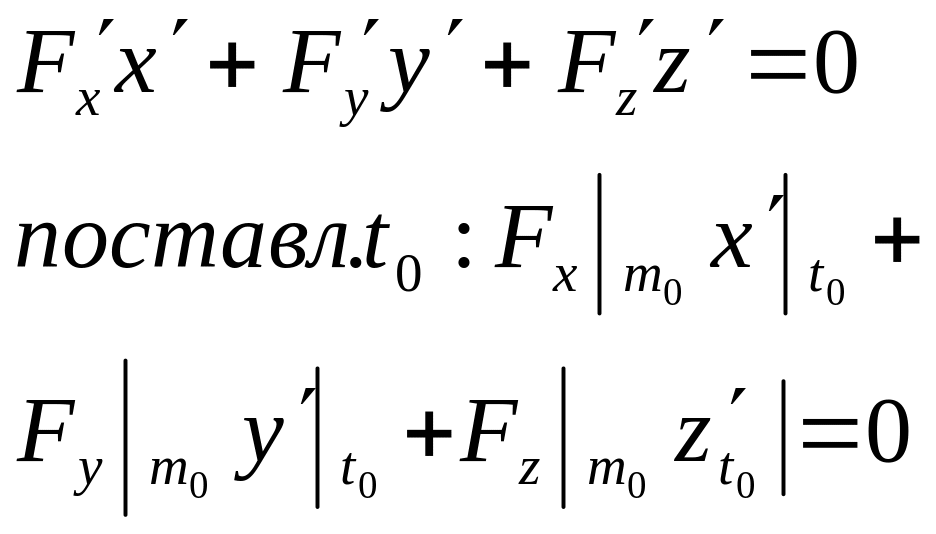 N=(F_x(M₀);F_y(M₀);F_z(M₀)) и A=(x(t₀);y(t₀);z(t₀))-скалярное произведение в-ов NA=0; NA=>A-касательн.вектор. N-зависит от F(x;y;z)=0 и (.)M₀,т.е. от поверхности, значит Nкасательн к кривым, проходящим через(.) M₀. нормаль- прямая касательной плоскости, проходящ через(.) касательной. ур.прямой(кононич) где х0, y0,z0-координ(.) и a_x,a_y,a_z-коорд.напрвляющ.вектора.

10.формула Тейлора для ф-и нескольких переменных.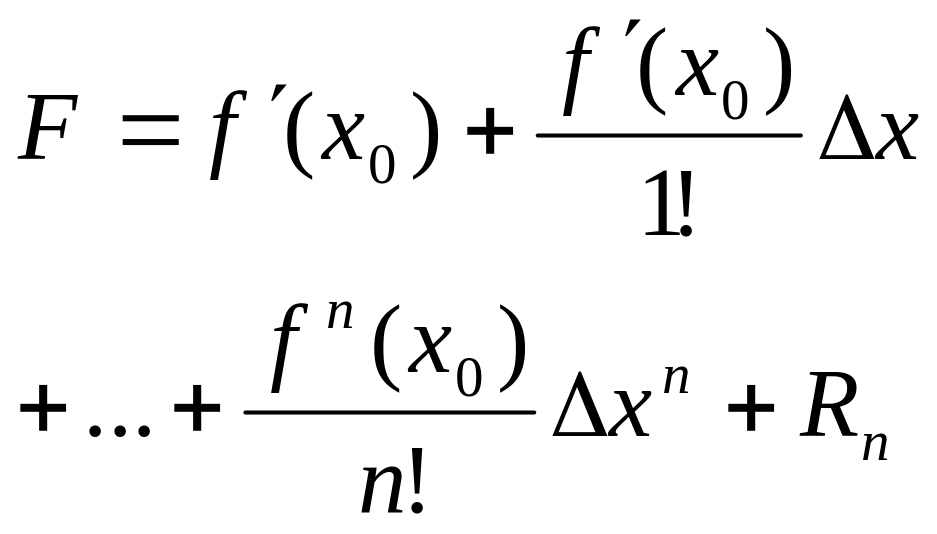 где ∆х=х-х₀

Х₀=0 тогда z=f(x,y)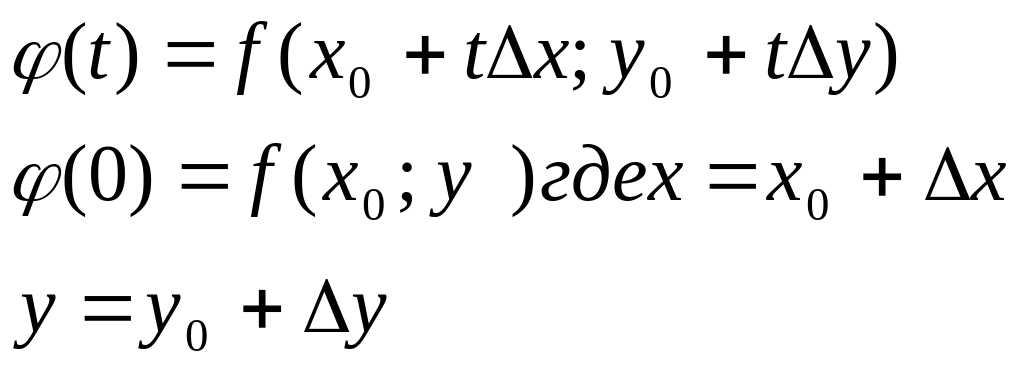 диф(х0,y0)вычисляется в (.)

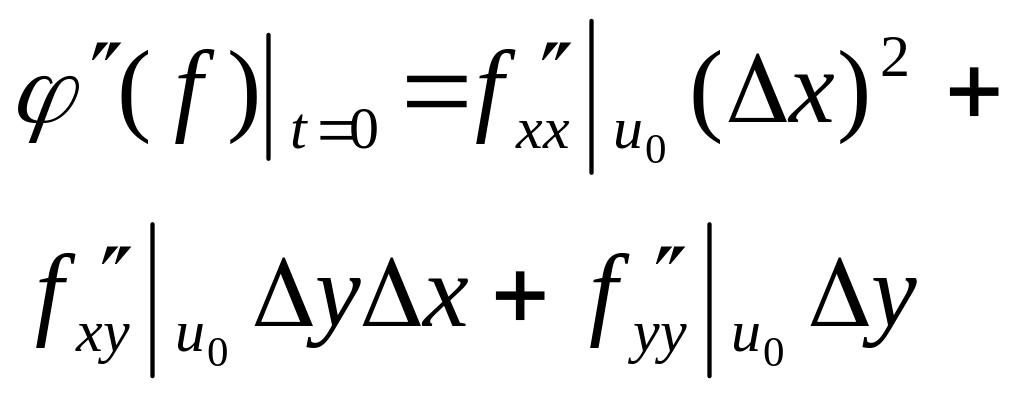
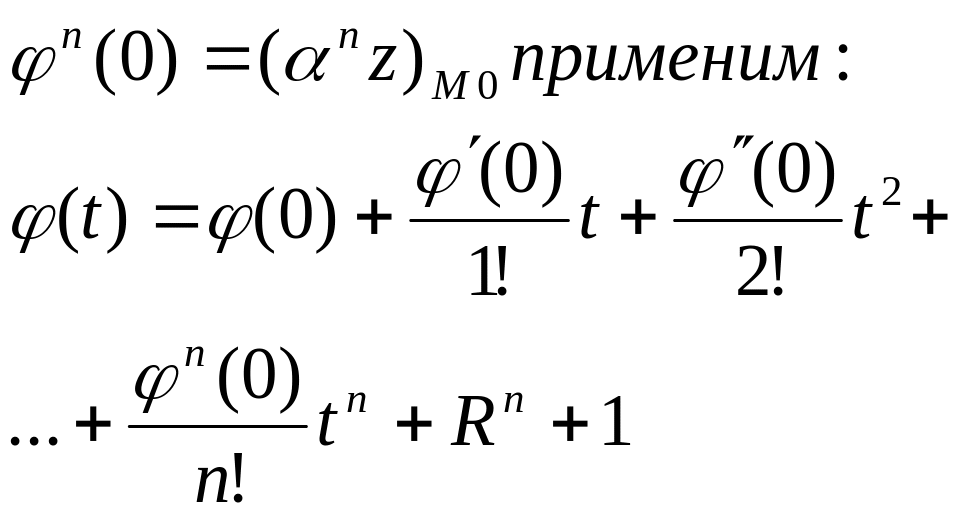
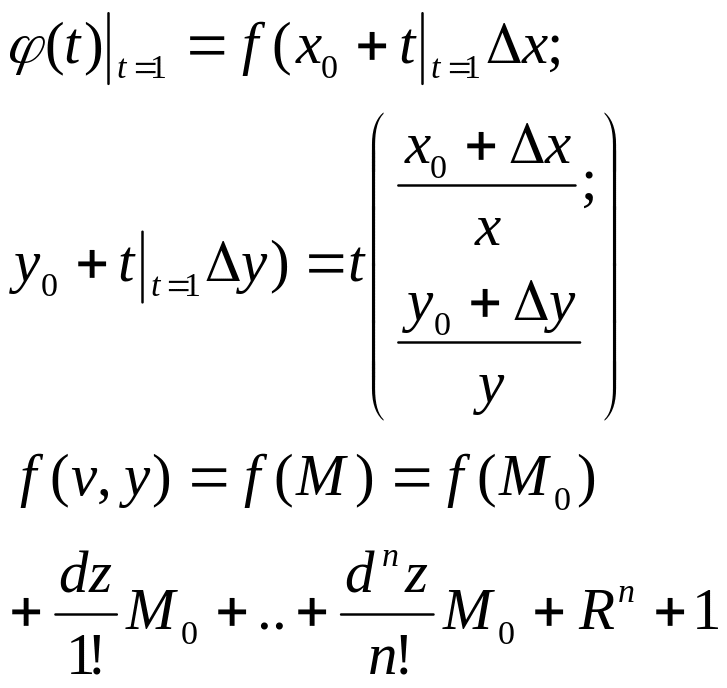-ф.Тейлора для ф.нескольких переменных

11.Необходимые условия экстремума ф-ии нескольких переменных.

(.)с-(.)локального min f-ии, если существует окрестность у этой (.), для всех(.) которой выполняется неравенство f(M)>f(с), где M (.)с- локальный max, если сущ.окрестность, для всех (.) которой выполняется неравенство f(M)<f(с) (.) в которой достигается лок min/max-(.) лок.экстремума, а гназениче- лок.экстремум f-ии. Необходимое условие экстремума: частные производные =0 (.) в которых выполняется это равенство-стационарные (.)

12. достаточные условия экстремума ф-ии для 2-х переменных. Остаток- бесконечно малое более высокого порядка, чем послднее слагаемое. Z=f(x,y) U₀(x0,y0)-критические (.) чем явл.М₀-? Предположим, что f дважды непрерывно диф. Запишим для f формулу Тейлора для М=2 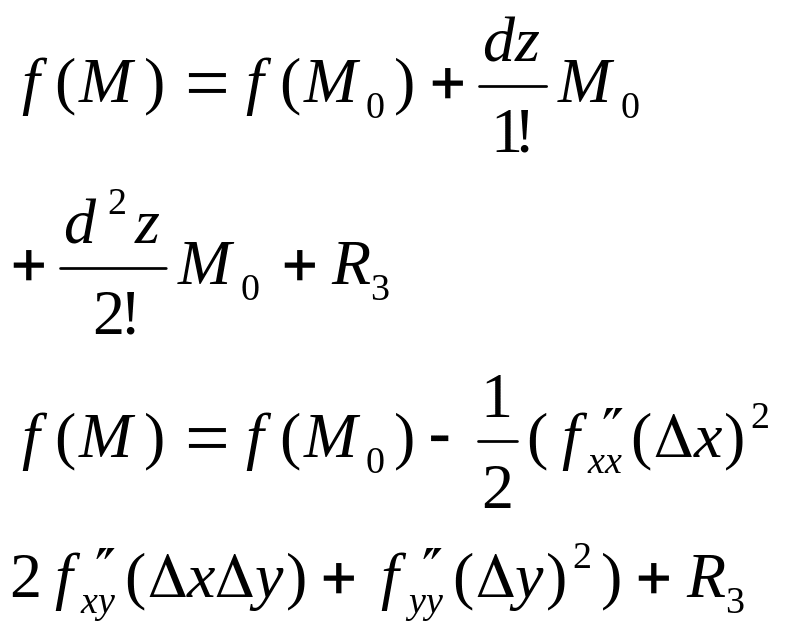1- если 2-й дифференциал положиельный при ∆х ,∆y0,то U₀-min. 2-если (d²z)<0, то U₀-max.3-если (d²z)имеет разные значения, то в (.)U_{0 ЭКСТРЕМУМА НЕТ!}

Пусть

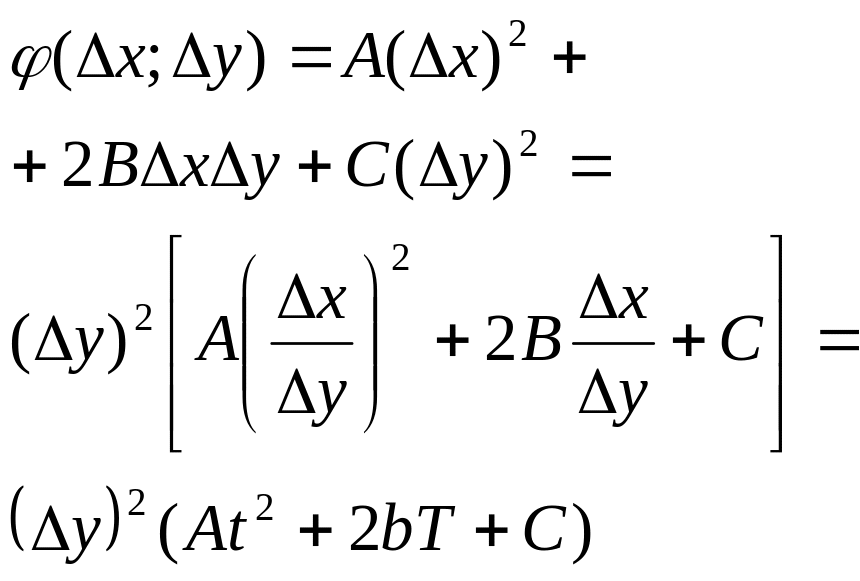D=(2B)²-4AC= =4(B²-AC); 1-B²-AC>0-имеет корни.2- B²-AC<0- или положительные или отрицательные значении. 3- B²-AC>0-экстремума нет в М₀-различные значения. При D=0 необходимы доп исследования при помощи 3-о диф.

13.Условный экстремум. Метод множителей Лагранжа. z=f(x;y)- extr (1)-найти экстр ф-ии f(x;y) если корд.точек удовлетвор.ур-ию g(x;y)=0 (2) G(x;y) определяет непрер-ую кривую лежащую в плоскости XY Найти extr ф-ии f(x;y) на кривой. Пример: z=2x+3y(1)-max (2) возможно у выразить из 2 и подставить в 1.ф-ия z будет зависеть только от переменной х. далее ф-ия исследуется методом мат анализа(произв=0 и тд) М₀(х₀;у₀)-точка extr (задача 1,2) то существ. ,что в М(х₀;у_{0; 0}) L_x’=0 L_y’=0 L ’=0 эта теорема дает необходимое условие extr. L=2x+3y+ (x²+y²+4); L_x’=2+2 x, x=-1/ ; L_y’=3+2 y, y=-3/2*1/ ; L ’=x²+y²-4 следовательно 1/ ²+9/4*1/ ²=4; 13/16= ² _1,2=± М₁ М₂ необх.условие,потенцильные extr. Множ-во D окружн радиуса 2,замкнутое и огранич множ-во=>ф-ия z имеет на нем свое ниб и наим знач. Наиб знач будет в М₂,наим в М₁ z_max=

14.Первообр.ф-ия и неопр.интегал.Таблица неопр.интегралов и их сво-ва. Пусть есть ф-ия f(x),опред. на некотором промежутке.Первообразной ф-ией F(x) для f(x) на промеж. Х назыв.ф-ия, производная от которой равняется заданной ф-ии. F’(x)=f(x) Теор. Если F и F₁ первообр.для ф-ии f на промежутке Х <=> F(х)-F₁(х)=const Док-во: F(х),F₁(х) две первообр. Составим их разность Х <=> ; F(х)-F₁(х)=const,F-перв.=> F₁(х)-перв. C¹(X)-множ-во ф-ий диф-мых на промеж. Х, введем отнош.эквив-сти F₁~ F₁ <=> F₁-F₂=c,обладающ. Всеми сво-ми рав-ва F~F, F₁~F₂=> F₂~ F₁, F₁~F₂ и F₂~F₃ => F₁~F₃.Неопр интеграл для ф-ии назыв множ-во всех первообр, т е множ-во таких ф-ий ={F(x)| F(x)’=f(x)}={F(x)+c, c R, F’(x)=f(x)}=F(x)+c Сво-ва: 1)линейности: ; ; Док-во: вычислим произв от левой части =f(x)+g(x) от правой части =

15. Замена переменной в неопр интеграле.Интегрирование по частям Т ф-ла подведения под знак диф-ла. И справа и слева стоит ф-ия зависящая от t (л.ч.)_t’= (пр.ч)_t’= ; (л.ч)’=(пр.ч)’ U(x),V(x) ф-ии диф-мые на множ-ве Х Док-во: (U(x)*V(x))’=U’(x)V(x)+V’(x)U(x) л.ч. пр.ч.