§7. Сведение игры двух лиц с нулевой суммой к линейной распределительной задаче.
Пусть дана матрица игры размерности m×n, в которой нет седловой точки и нет возможности сократить размерность матрицы
. (1)
Такая конечная игра двух лиц с нулевой суммой, любой размерности может быть представлена как задача линейного программирования и, наоборот, каждая задача линейного программирования может быть представлена как матричная игра.
Пусть матрица (1) не содержит седловой точки, решение игры запишем в смешанных стратегиях:
,
.
Пусть первый игрок А применяет свою оптимальную стратегию , а второй игрок В использует последовательно свои чистые стратегии. Тогда первый игрок может выиграть не меньше чем цена игры. Поэтому будут выполняться неравенства:
(2)
Хотя пока цена игры неизвестна, однако можно считать V>0. Это условие всегда выполняется, если элементы матрицы сделать неотрицательными, а этого можно достичь, прибавляя ко всем элементам матрицы (1) положительное число. После определения цены игры это число из цены игры надо вычесть. Решение игры при таком преобразовании матрицы не меняется.
Разделим все неравенства системы (2) на V
Введем
обозначения
В результате получим систему неравенств
(3)
Так
как по условию задачи
- вероятности того, что первый игрок А
будет пользоваться своей i-й
чистой стратегией (
=1,2,
. . ., m)
,
то
.
Подставим
вместо
значение
,
получим
,
или
.
Для первого игрока А цену игры V надо максимизировать. Если обозначим
,
то эту функцию Z надо минимизировать. В результате получаем задачу линейного программирования с целевой функцией
и
ограничениями (3) и
.
Решая
такую задачу, находим значение
и величину
,
а затем можем найти
.
Аналогичным образом можно получить задачу линейного программирования для нахождения вероятностей оптимальной стратегии для второго игрока В. Для этого предполагаем, что второй игрок В пользуется своей оптимальной смешанной стратегией, а первый игрок А поочередно пользуется своими чистыми стратегиями. Тогда второй игрок не может проиграть больше чем цена игры V по основной теореме теории игр.
При таких предположениях для определения стратегии игрока В запишем следующие условия:
(4)
Разделив все члены неравенств на V, получим
(5)
где
.
Переменные
должны быть выбраны так, чтобы они
удовлетворяли неравенствам (5) и целевая
функция
(6)
достигала максимума, так как второй игрок В стремится как можно меньше проиграть.
В результате мы получаем пару двойственных симметричных задач линейного программирования. Используя свойство симметричности, решаем наиболее удобную из них, т.е. требующую меньших вычислений, а решение второй задачи находим из условия оптимального плана двойственной задачи.
Пример 1. (Планирование посева).
Сельскохозяйственное
предприятие имеет возможность выращивать
две культуры
и
.
Необходимо определить, как сеять эти
культуры, если при прочих равных условиях
их урожаи зависят от погоды, а план
посева должен обеспечить наибольший
доход, определяемый полученной прибылью
от реализации выращенной культуры,
определяется полученным объемом. В зоне
рискованного земледелия планирование
посева должно осуществляться с учетом
наименее благоприятного состояния
погоды.
Таким образом, одной из сторон выступает сельхозпредприятие, заинтересованное в том, чтобы получить наибольший доход. Это первый игрок А, а другой стороной выступает природа В, способная навредить сельхозпредприятию в максимальной степени с помощью погодных условий цели которой противоположны.
Принятие природы за противника равносильно планированию посева с учетом наиболее неблагоприятных условий; если же погодные условия окажутся благоприятными, то выбранный план даст возможность увеличить доход. Это антагонистический конфликт. У первого игрока две стратегии и . У второго игрока, предположим, три стратегии: - засушливое лето; - нормальное лето и - дождливое лето.
В качестве выигрыша игрока А возьмем прибыль от реализации полученной продукции в млн. рублей в зависимости от состояний погоды.
При выборе первым игроком А своей чистой стратегии предположим, что прибыль составит 7, 6 и 4 млн. руб. от реализации продукции, при соответствующих стратегиях второго игрока В: , , . Аналогично, при выборе игроком А второй стратегии прибыль составит 2, 5 и 6 млн. руб. при соответствующих стратегиях второго игрока , , .
Результаты сведены в матрицу
.
Решение. Проверим, есть ли седловая точка:
α=max(4;2)=4; β=min(7;6;6)=6;
α≠β, следовательно, нет седловой точки. Цена игры 4≤V≤6.
Решение ищем в смешанных стратегиях. Применим графический метод
у В1
В2
В3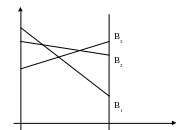
Нижнюю границу игры образуют стратегии и . Тогда матрица примет вид
.
И решение:
Оптимальная смешанная стратегия игрока А
.
Для второго игрока
-
оптимальная стратегия игрока В.
Цена игры
.
Полученные
результаты можно истолковать так: на
всех площадей выращивать культуру
,
а на
всех площадей выращивать культуру
,
в результате чего прибыль предприятия
будет не меньше чем 4.857 млн. рублей.
Пример 2. (Переговоры о заключении контракта между профсоюзом и администрацией).
Предположим, что администрация предприятия ведет переговоры с профсоюзом рабочих и служащих о заключении контракта.
Предположим, что платежная матрица, отражающая интересы договаривающихся сторон, имеет следующий вид
.
Выплаты указаны в рублях и представляют собой среднюю зарплату рабочих и служащих. Эта матрица описывает прибыль профсоюза – игрок А и затраты администрации – игрок В. Ясно, что профсоюз стремится максимизировать доходы рабочих и служащих, в то время как администрация старается минимизировать свои потери.
Решение. Проверим, есть ли седловая точка:
α=max(60;50;50;55)=60; β=min(100;110;70;65)=65;
α≠β, нет седловой точки. Цена игры V
60≤V≤65.
Проведем анализ. Для первого игрока вторая стратегия по отношению к первой и третья по отношению к четвертой не выгодны так как их элементы меньше соответствующих элементов первой и четвертой стратегий. В результате получим эквивалентную матрицу
.
Для второго игрока не выгодны первая и вторая стратегии, так как их элементы больше чем соответствующие элементы третьей и четвертой стратегий. В результате получим эквивалентную матрицу
.
Так как из всех элементов можно вычесть 55, то получим матрицу
,
Тогда решение будет
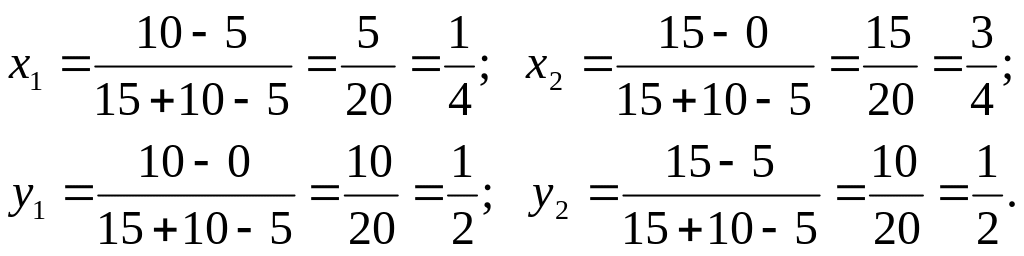
Оптимальные решения
.
Цена игры
.
Вывод: Профсоюзу следует выбирать стратегию в 25% случаев и стратегию в 75%.
Администрации следует выбрать стратегию с вероятностью 0.5 и стратегию также с вероятностью 0.5. При этом ожидаемая цена игры равна 62.5.
Пример 3. (Военный конфликт).
Предположим, что между двумя государствами А и В идет военный конфликт в течение 30 дней.
Для бомбардировки моста страны В – страна А использует два имеющихся самолета. Разрушенный мост восстанавливается в течение суток, а каждый самолет совершает один полет в день по одному из двух воздушных маршрутов, соединяющих эти страны. У страны В есть два зенитных орудия, при помощи которых можно сбивать самолеты страны А. Если самолет собьют, то некая третья страна в течение суток поставит стране А новый самолет.
Правило игры: страна А может послать самолеты либо по одному маршруту, либо по разным.
Страна В может поместить либо обе зенитки на одном маршруте, либо по одной зенитке на каждом маршруте.
Если один самолет летит по маршруту, на котором расположена одна зенитка, то этот самолет будет сбит.
Если два самолета летят по одному маршруту, на котором расположены две зенитки, то оба самолета будут сбиты.
Если два самолета летят по маршруту, на котором расположена одна зенитка, то сбит будет только один самолет.
Если самолет доберется до цели, то мост будет уничтожен.
Решение. У страны А есть две стратегии:
- послать самолеты по разным маршрутам - ;
- послать самолеты по одному маршруту - .
У страны В также две стратегии:
- поместить зенитки на разных маршрутах - ;
- поместить зенитки на одном маршруте - .
Если страна А выберет стратегию , а страна В – стратегию , то страна А получит нулевой выигрыш, так как ни один из самолетов не достигнет цели.
Если страна А выберет стратегию , а страна В – стратегию , то хотя бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.
Если страна А выберет стратегию , а страна В – стратегию , то вновь хотя бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.
Если
страна А
выберет стратегию
,
а страна В
– стратегию
,
то страна А
с вероятностью
выберет маршрут, на котором установлены
зенитки, и, следовательно, цель будет
уничтожена с вероятностью
.
Запишем результаты проведенного анализа в стандартной игровой форме:
.
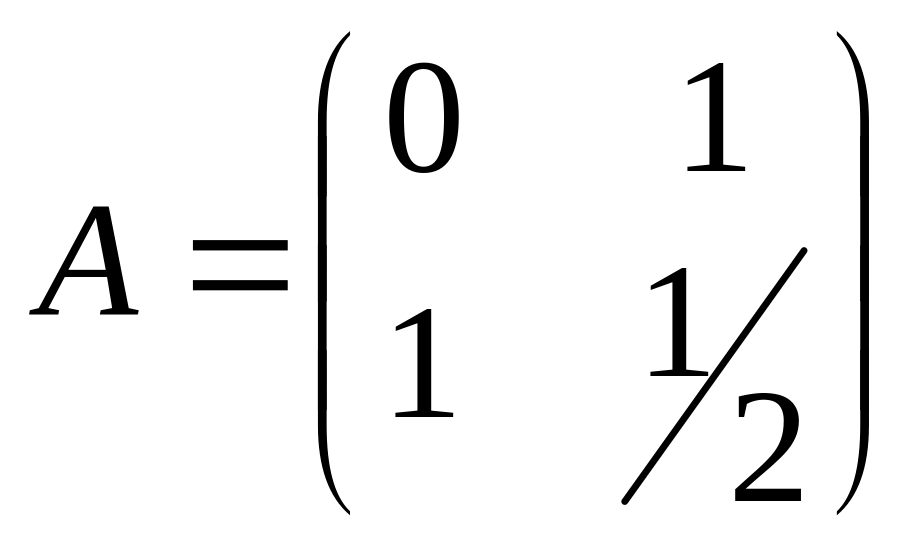По формулам игры 2×2 найдем оптимальные стратегии обоих игроков, так как нет седловой точки
α= ; β=1; ≤V≤1.
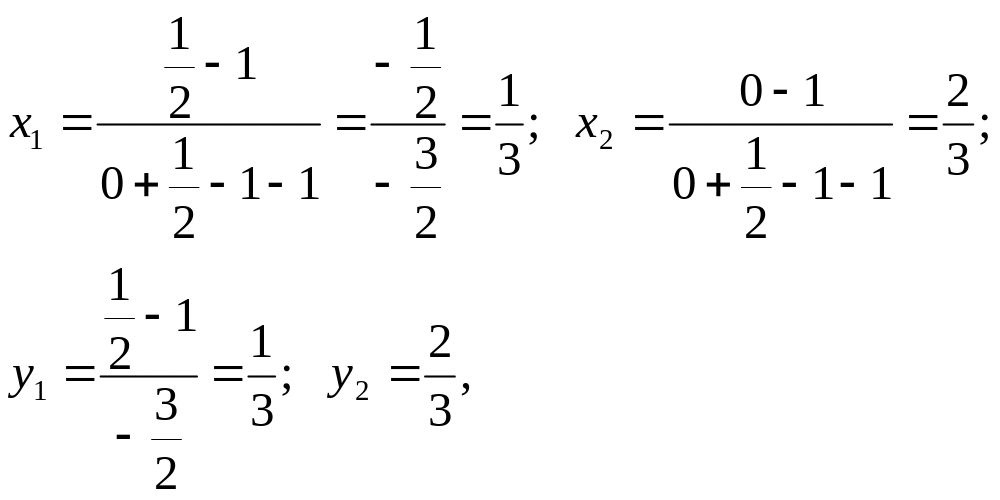
поэтому
.
Цена
игры
.
Вывод: если сторона А будет посылать самолеты по разным маршрутам в течении десяти дней из тридцати, отпущенных на войну, и по одному маршруту в течение двадцати дней, то в среднем она будет иметь 66.7% удачных случаев, т.е. мост будет находиться в нерабочем состоянии.
Воспользовавшись для своих зениток предложенным выбором, страна В не позволит бомбить мост чаще, чем в 66.7% случаев.
Пример 4. Решить игру заданную матрицей
.
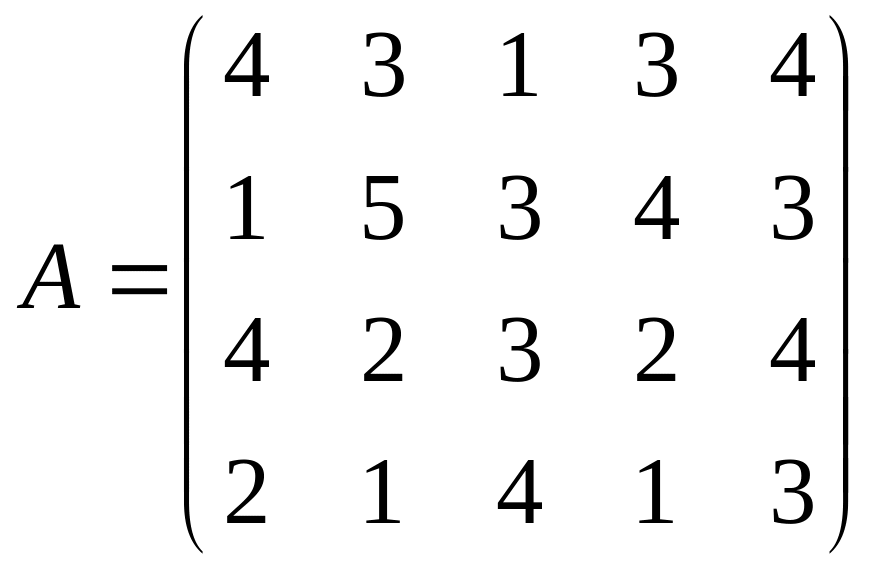Решение. Проверим, есть ли седловая точка
α=max(1;1;2;1)=2; β=min(4;5;4;4;4)=4;
α≠β, нет седловой точки.
Проверим, нельзя ли уменьшить размерность матрицы. Для первого игрока нет пассивных стратегий. Для второго игрока пятая стратегия невыгодная, так как элементы пятого столбца больше или равны соответствующих элементов первого столбца. В результате получаем эквивалентную матрицу
.
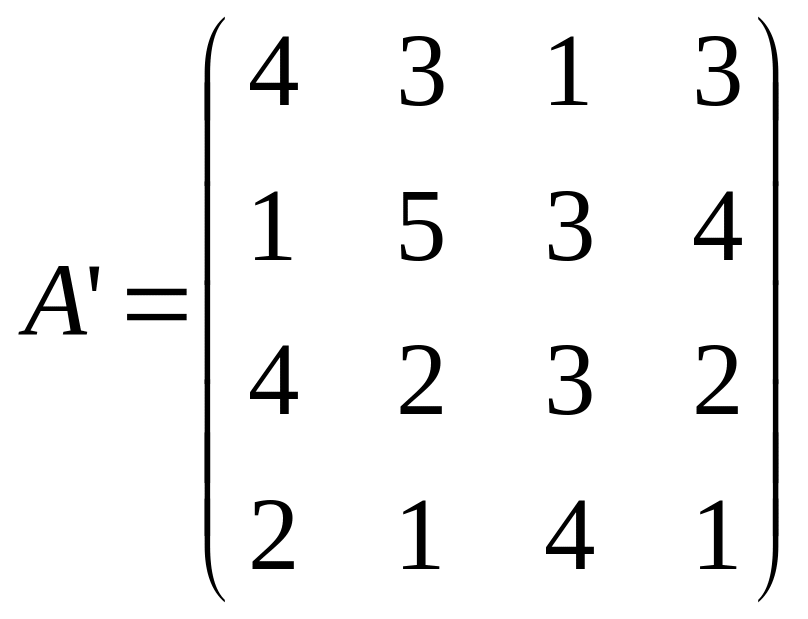Решение ищем в смешанных стратегиях
и
.
Сведем решение игры к паре симметрических двойственных задач линейного программирования.
Для определения оптимальной стратегии первого игрока А получим следующую задачу линейного программирования:
Найти
при ограничениях
Двойственная задача для определения оптимальной стратегии игрока В формулируется так
Найти
при ограничениях
В
первой задаче
,
во второй
.
Решим
вторую задачу симплексным методом. Для
этого воспользуемся дополнительными
неизвестными
и запишем задачу в виде:
при ограничениях
Первоначальный
базис образуют единичные векторы
.
Для решения этой задачи линейного
программирования воспользуемся симплекс
– методом.
i |
базис |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||
1 |
|
0 |
1 |
4 |
3 |
1 |
3 |
1 |
0 |
0 |
0 |
2 |
|
0 |
1 |
1 |
5 |
3 |
4 |
0 |
1 |
0 |
0 |
3 |
|
0 |
1 |
4 |
2 |
3 |
2 |
0 |
0 |
1 |
0 |
4 |
|
0 |
1 |
2 |
1 |
4 |
1 |
0 |
0 |
0 |
1 |
m+1 |
|
0 |
-1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
|
1 |
|
0 |
|
|
0 |
|
|
1 |
|
0 |
0 |
2 |
|
1 |
|
|
1 |
|
|
0 |
|
0 |
0 |
3 |
|
0 |
|
|
0 |
|
|
0 |
|
1 |
0 |
4 |
|
0 |
|
|
0 |
|
|
0 |
|
0 |
1 |
m+1 |
|
|
|
0 |
|
|
0 |
|
0 |
0 |
|
1 |
|
1 |
|
1 |
0 |
|
|
|
|
0 |
0 |
2 |
|
1 |
|
0 |
1 |
|
|
|
|
0 |
0 |
3 |
|
0 |
|
0 |
0 |
|
|
|
|
1 |
0 |
4 |
|
0 |
|
0 |
0 |
|
|
|
|
0 |
1 |
m+1 |
|
|
0 |
0 |
|
|
|
|
0 |
0 |
|
1 |
|
1 |
|
1 |
0 |
0 |
|
|
|
|
0 |
2 |
|
1 |
|
0 |
1 |
0 |
|
|
|
|
0 |
3 |
|
1 |
|
0 |
0 |
1 |
|
|
|
|
0 |
4 |
|
0 |
|
0 |
0 |
0 |
|
1 |
|
|
1 |
m+1 |
|
|
0 |
0 |
0 |
|
0 |
|
|
0 |
|
1 |
|
1 |
|
1 |
|
0 |
0 |
|
|
|
0 |
2 |
|
1 |
|
0 |
|
0 |
1 |
|
|
|
0 |
3 |
|
1 |
|
0 |
|
1 |
0 |
|
|
|
0 |
4 |
|
1 |
|
0 |
|
0 |
0 |
|
|
|
1 |
m+1 |
|
|
0 |
|
0 |
0 |
|
|
|
0 |
|
В результате 4 итераций получили оптимальное решение:
Так
как
,
то цена игры
,
с учетом того, что
получим
.
Таким образом, оптимальная стратегия второго игрока В будет
.
При
этом он проиграет
.
Теперь используя двойственность, получим оптимальную стратегию первого игрока из условия
,
с
учетом того, что
получим
или
,
при этом он выиграет .