§6. Решение игр вида 2×n и m×2.

Игры с матрицами

или

не имеющих седловых точек можно решать, используя графическое построение стратегий игроков, использованное в §4 при графическом решении игры 2×2. Для этого, предположим, что один из игроков имеет только две стратегии, а другой больше двух, т.е. рассмотрим игру вида 2×n. Запишем эту игру в таблицу в предположении, что первый игрок использует свою смешанную стратегию , где , и пусть эта игра не имеет седловой точки.

			. . .
			. . .
			. . .

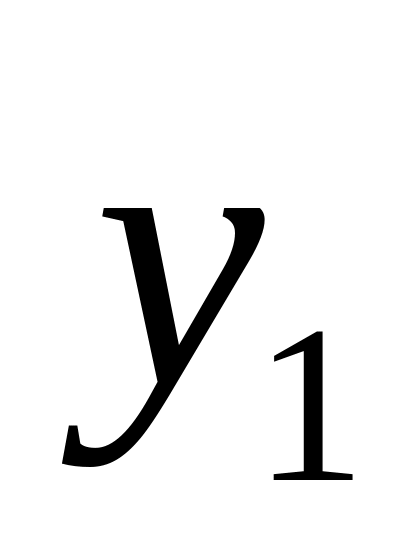
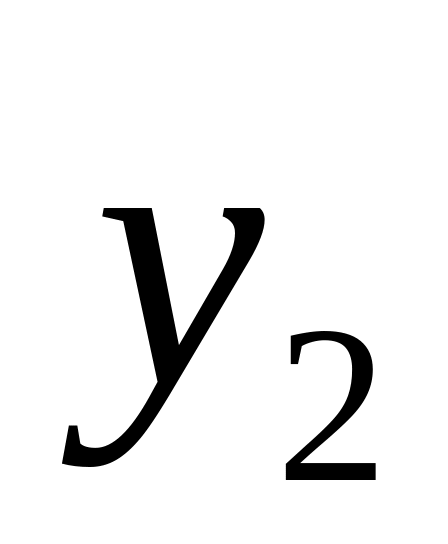
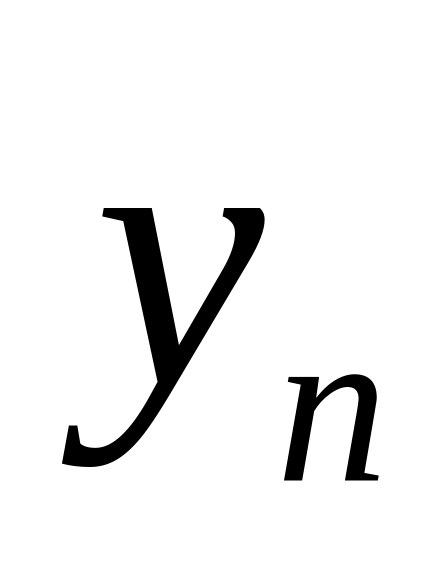
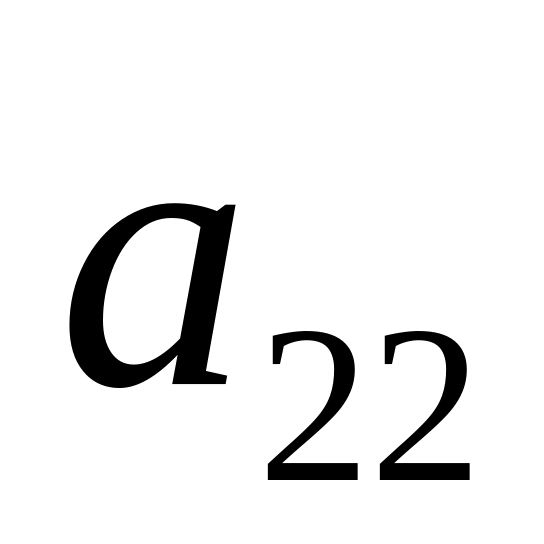
Если второй игрок использует свою чистую первую стратегию, то ожидаемый выигрыш первого игрока составит

,

если второй игрок воспользуется своей второй чистой стратегией, а первый продолжает пользоваться своей смешанной стратегией, то выигрыш первого игрока составит , и т.д.

Из этих равенств видно, что ожидаемый выигрыш первого игрока линейно зависит от .

В соответствии с критерием минимакса для игр в смешанных стратегиях первый игрок должен выбирать так, чтобы максимизировать свой минимальный ожидаемый выигрыш. Эта задача может быть решена графически построением прямых линий, соответствующих линейным функциям от переменной .

Эту процедуру рассмотрим в начале в общем виде. Таким образом, используя геометрическую интерпретацию, находят решение игры 2×n следующим образом. Каждой из n стратегий второго игрока В соответствует прямая . Построив эти прямые, находим нижнюю границу выигрыша. Ордината точки K, лежащая на нижней границе, для которой величина выигрыша наибольшая, определяет цену игры и ее решение.

При этом определяются активные стратегии игрока В, использование которых дает второму игроку В возможность проиграть наименьшее значение. Соответствующие активным стратегиям прямые пересекаются в точке K и образуют нижнюю цену игры.

А₁

Рис.7

А₂

y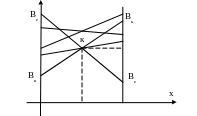

Из геометрических соображений можно найти значения , соответствующие активным стратегиям игрока В. Это на нашем чертеже и (рис.7).

Пример 1. Найти решение и цену игры заданной матрицей

.

Решение. Найдем нижнюю и верхнюю цену игры.

α=max(2;2)=2; β=min(5;4;4;5)=4; 2≤V≤4.

Построим систему координат и проведем на расстоянии единицы от начала координат перпендикуляр к оси Ox. Построим прямую , отложив на оси Oy 3 единицы масштаба, а на перпендикуляре 5 единиц. Затем аналогично , , . Получим:

у

Рис.8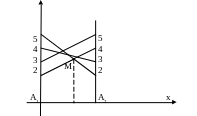

Ломанная соответствует нижней границе выигрыша. Оптимальные стратегии игрока В – третья и четвертая. В результате получим эквивалентную исходной матрице матрицу (рис.8).

.

Решая эту игру по формулам §3, получим:

.

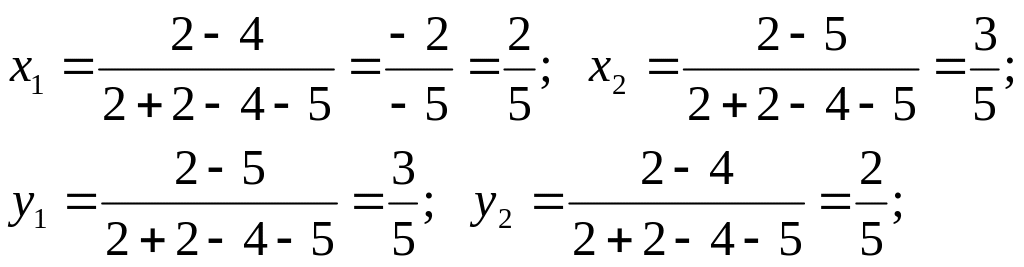
Тогда оптимальные стратегии обоих игроков можно записать, придав пассивным стратегиям значения вероятностей равными нулю:

.

При таком решении цена игры .

Аналогично может быть рассмотрена игра m×2. Только в этом случае строят верхнюю границу игры, которая также является ломанной состоящей из прямых расположенных выше всех остальных. Самая нижняя точка этой ломанной определяет цену игры. А с помощью стратегий, образующих верхнюю границу игры можно найти оптимальные стратегии обоих игроков. Рассмотрим этот случай на примере.

Пример 2. Найти решение игры, заданной матрицей

.

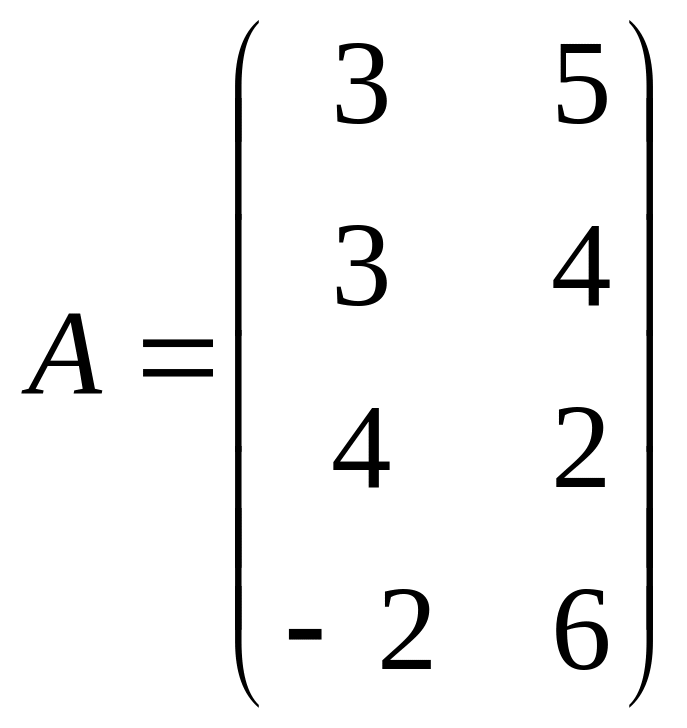Решение. Эта игра не имеет седловой точки, так как

α=max(3;3;2;-2)=3; β=min(4;6)=4; 3≤V≤4.

Пусть и смешанные стратегии второго игрока. Запишем ожидаемые проигрыши второго игрока в таблицу

Чистые стратегии первого игрока	Ожидаемые проигрыши второго игрока
1
2
3
4

Изобразим четыре прямые в системе координат

Здесь верхнюю границу игры образуют три стратегии 1, 3, и 4. Минимаксная точка определяется как самая нижняя точка K на огибающей ломанной сверху. Ордината этой точки есть цена игры, а абсцисса основания перпендикуляра опущенного из этой точки K на ось абсцисс есть значение . Точка K результат пересечения первой и третьей стратегий, т.е.

Тогда

Подставим это значение в одно из уравнений прямых 1 или 3, получим:

.

Прямые пересекающиеся в минимаксной точке, соответствуют чистым стратегиям 1 и 3 первого игрока А. Это означает, что , следовательно, и эквивалентная матрица имеет вид (рис.10)

.

Можно записать теперь ожидаемый выигрыш первого игрока, соответствующий чистым стратегиям второго игрока в таблицу:

Чистые стратегии второго игрока	Ожидаемые выигрыши первого игрока
1
2

Найдем значение из равенства

Тогда

Таким образом, оптимальной стратегией первого игрока будет

.

Эта стратегия также дает цену игры .

Ответ: