
- •Содержание
- •Введение.
- •§1. Основные определения и понятия.
- •§2. Классификация игр.
- •§3. Игра двух сторон с нулевой суммой.
- •§4. Графическое решение игры 2×2.
- •§5. Упрощение игры.
- •§6. Решение игр вида 2×n и m×2.
- •§7. Сведение игры двух лиц с нулевой суммой к линейной распределительной задаче.
- •Упражнения.
- •Литература.
§5. Упрощение игры.
Задача решения игры, если ее матрица не содержит седловой точки тем сложнее, чем больше значений m и n, т.е. матрица игры имеет размерность m×n, m>2, n>2.
В связи с этим возникает вопрос: нельзя ли сократить размерность матрицы так, чтобы это сокращение не повлияло на решение игры и на цену этой игры. Оказывается можно. Для этого существует принцип доминирования, который позволяет в некоторых случаях игру с матрицей большего размера свести к игре с матрицей меньшего размера.
Пусть матрица игры размерности m×n
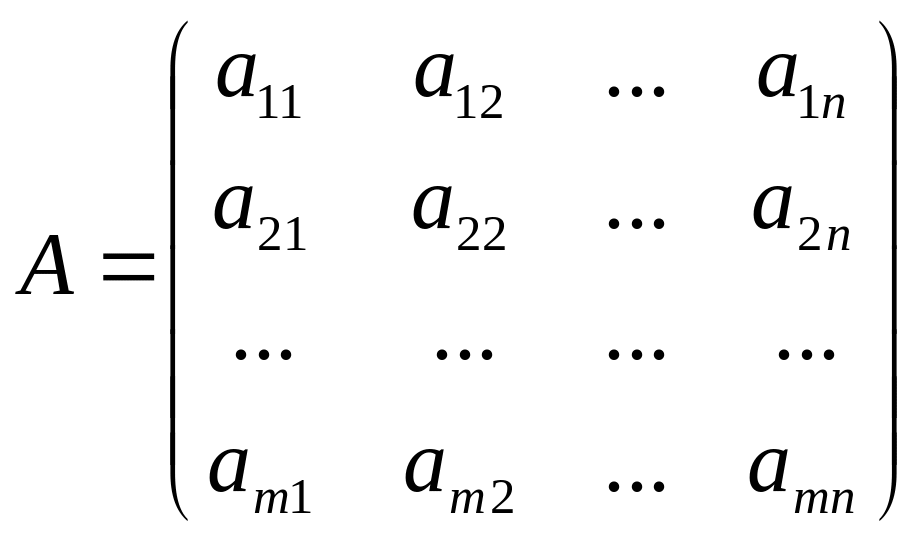
не имеет седловой точки, т.е. α≠β. Тогда ее решение нужно искать в смешанных стратегиях
![]() и
и
![]() .
.
Говорят,
что некоторая стратегия
первого игрока А
доминируется некоторой другой стратегией
![]() первого игрока А,
если все элементы i-й
строки не больше соответствующих
элементов k-й
строки, а именно
первого игрока А,
если все элементы i-й
строки не больше соответствующих
элементов k-й
строки, а именно
![]() .
.
Аналогичное
определение можно привести и для
стратегии второго игрока В,
а именно некоторая стратегия
второго игрока В
доминируется некоторой другой стратегией
![]() второго игрока, если все элементы j-го
столбца не меньше соответствующих
элементов l-го
столбца, а именно
второго игрока, если все элементы j-го
столбца не меньше соответствующих
элементов l-го
столбца, а именно
![]() .
.
Доминирование представляет отношение между стратегиями, наличие которого во многих случаях дает возможность сократить размеры исходной платежной матрицы игры. Это следует из того факта, что доминируемые стратегии могут быть исключены, как невыгодные игрокам, при этом цена игры не изменится.
Пример 1. Пусть дана матрица игры
![]() .
.
Сократить размерность и найти цену игры.
Решение. Начнем рассуждения за второго игрока. С его позиции сравнивая стратегию с видим, что третья стратегия выгоднее чем вторая поскольку минимальный проигрыш второго игрока В при использовании им стратегии составит три единицы, а максимальный четыре единицы, а при использовании стратегии минимальный составит -2, а максимальный одну единицу. Другими словами элементы второго столбца больше соответствующих элементов третьего столбца, поэтому исходя из позиции второго игрока В можно предположить, что он не будет пользоваться своей чистой второй стратегией , так как он может проиграть больше чем мог бы. Поэтому второй столбец можно вычеркнуть. В результате получим эквивалентную матрицу
![]() .
.
С позиции первого игрока А его первая стратегия хуже второй, так как по первой стратегии он только проигрывает. Поэтому первую стратегию можно исключить. В результате получим матрицу
![]() .
.
Если теперь учесть интересы второго игрока В, то следует оставить только его первую стратегию, так как по второй стратегии он проиграет 1 (единицу), а по первой только 0 (ноль). Таким образом, получаем матрицу
![]() .
.
Это
есть цена игры V=0
и решение в чистых стратегиях
![]() .
.
Такой же результат получается, если использовать минимаксную стратегию:
α=max(-2;0)=0; β=min(0;3;1)=0;
α=β=V=0.
Пример 2. Сократить размерность матрицы
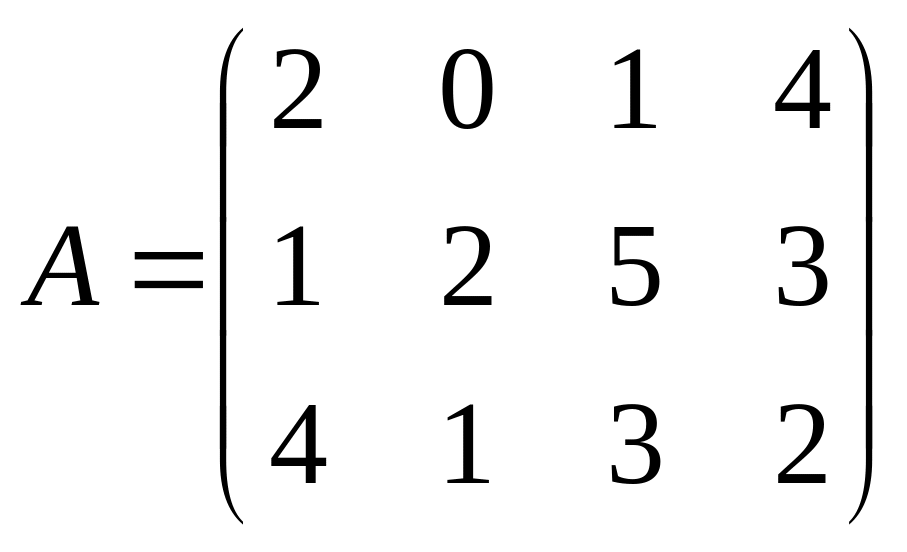 .
.
α=max(0;1;1)=1; β=min(4;2;5;4)=2;
1<V<2. Нет седловой точки.
Решение. Сравним четвертый столбец со вторым. Все элементы больше соответствующих элементов , поэтому с позиции второго игрока четвертая стратегия ему не выгодна. В результате получим матрицу
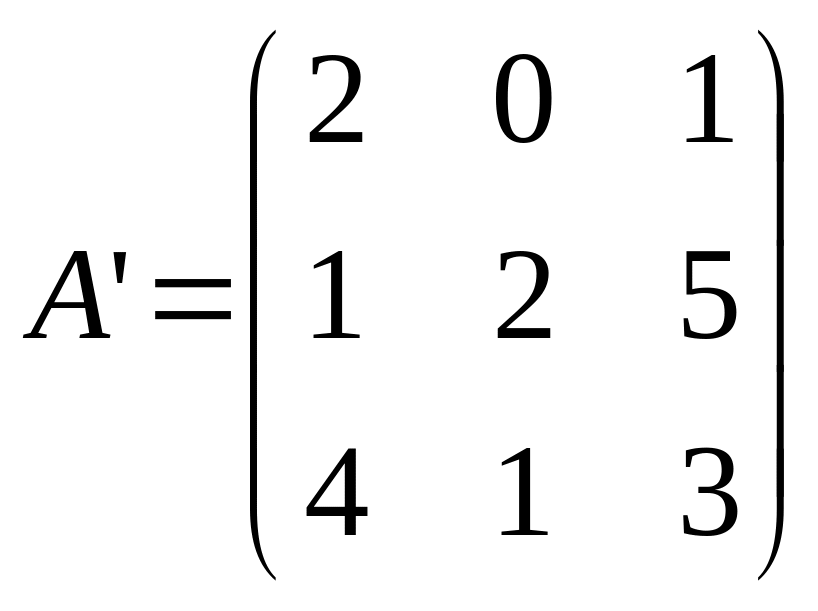 .
.
Теперь сравним третью строку с первой. Видим, что элементы первой строки меньше соответствующих элементов третьей строки. С позиции первого игрока стратегия не выгодна, поэтому ее можно вычеркнуть. Получим
![]() .
.
Теперь сравним с . Для второго игрока третья стратегия невыгодна, так как он может по этой стратегии проиграть больше чем мог бы. Получим
![]() .
.
Эту игру легко решить, используя формулы предыдущего параграфа:

Решение исходной игры в смешанных стратегиях запишется так
![]() ;
;
![]() .
.
При таком решении игры цена игры
![]() .
.
Пример 3. Сократить размерность матрицы
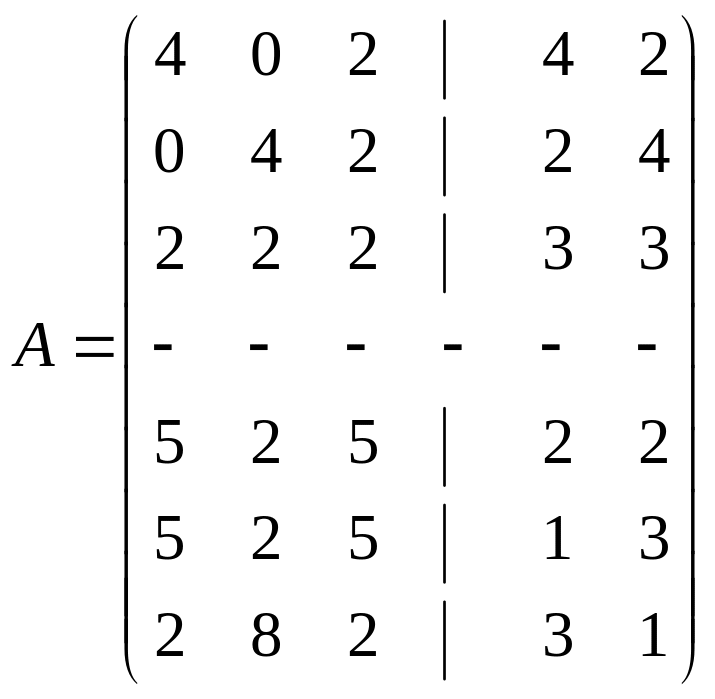 .
.
и найти решение и цену игры.
Решение. Найдем нижнюю и верхнюю цены игры.
α=max(0;0;2;2;1;1)=2; β=min(5;8;5;4;4)=4; 2≤V≤4.
Объединяем
стратегии
и
;
![]()
![]() и
и
![]() ;
и
;
и
;
и
;
и![]() и делим на число объединенных стратегий.
В результате получим эквивалентную
матрицу
и делим на число объединенных стратегий.
В результате получим эквивалентную
матрицу
![]() .
.
Найдем значение вероятностей по формулам

Цена игры
![]()
Оптимальные стратегии обоих игроков для первоначальной матрицы запишутся так
![]()
