§4. Графическое решение игры 2×2.

Пусть игра задана матрицей . Эту игру 2×2 можно решить графически. Для этого в прямоугольной системе координат на плоскости на оси абсцисс откладываем отрезок равный единице. Левый конец x=0, полученного отрезка на оси абсцисс соответствует стратегии для первого игрока А, а правый конец стратегии . Промежуточные точки x отрезка (0,1) соответствуют некоторым смешанным стратегиям , где . На концах выбранного отрезка проведем прямые, перпендикулярные оси Ox. На них будем откладывать выигрыш при использовании чистых стратегий игроком А. Если игрок В использует свою чистую стратегию , то выигрыш первого игрока при использовании чистой стратегии составит , а при использовании второй стратегии выигрыш составит . Отложим эти точки на вертикалях и соединим полученные точки отрезком прямой (Рис. 1).

у

x

C₁₁

Если первый игрок А применяет смешанную стратегию x, то его выигрыш при использовании вторым игроком своей чистой стратегии , составит ординату точки М лежащей на прямой .

Аналогично можно построить отрезок прямой (Рис. 2).

А₁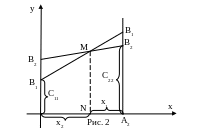

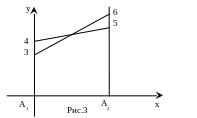
Если матрица игры имеет седловую точку, то в этом случае цена игры соответствует наивысшей ординате нижней из этих линий. Например, если матрица игры имеет

α=max(3;5)=5; β=min(6;5)=5; V=5,

то имеем решение ; V=5 (Рис.3).

Пусть α≠β, тогда α≤V≤β и графически это выглядит так, если матрица игры .

А₁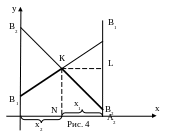

Ломанная является нижней границей игры, получаемой первым игроком А. Точка К, в которой ордината максимальна, определяет цену игры, а отрезки оси Ox от основания перпендикуляра отпущенного из точки К на ось Ox определяют оптимальные значения вероятностей и :

Для нахождения оптимальной стратегии игрока В можно воспользоваться формулами . Тогда

Подставим значения, получим

(1)

Подставим полученные значения и в равенство , получим тождество

Если в (1) подставим значение V, полученное в предыдущем параграфе:

получим значения и совпадающие с формулами (14).

Аналогичным образом можно рассмотреть минимизацию верхней границы выигрыша для игрока В. Для этого поменяем местами игроков А и В.

На левой вертикали откладываем значения проигрыша второго игрока В в случае применения им своей чистой первой стратегии , а на правой вертикали значения проигрыша при использовании чистой стратегии . В результате получим отрезок прямой в случае использования первым игроком А своей чистой стратегии , аналогично .

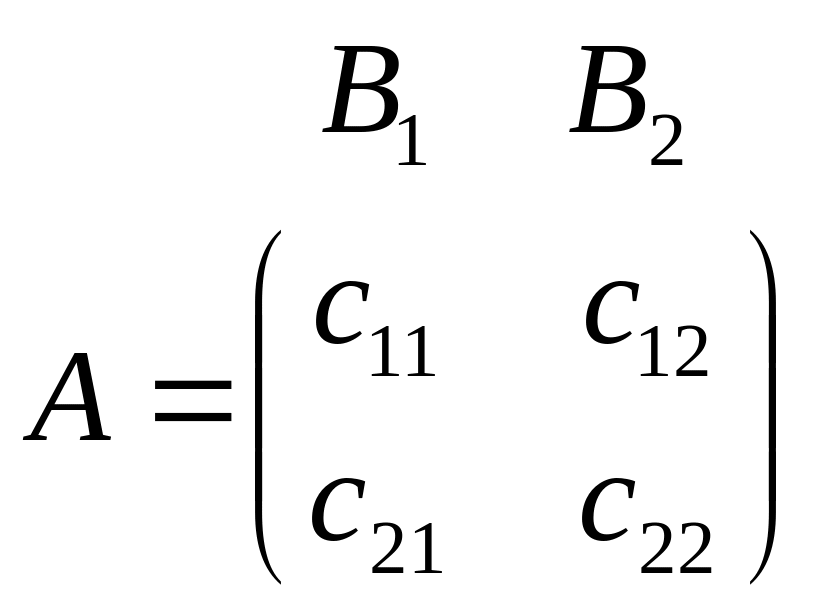
А₁

А₂

В₁

В₂

х

Рис.5

М₁

Ломанная является верхней ценой игры получаемой вторым игроком В. Точка , в которой ордината минимальна, определяет цену игры, а величины и определяют вероятности оптимальной стратегии второго игрока В (Рис.5).

Пример. Построить верхнюю цену игры

.

Р

х

ешение. На оси абсцисс отложим отрезок единичной длины и проведем из концов отрезка вертикали. На левой вертикали будем откладывать 5 единиц масштаба, а на правой 4 единицы. Эти значения соответствуют для решений и . Соединив эти точки, получим отрезок . Любая точка этого отрезка соответствует величине проигрыша второго игрока в случае использования им различных смешанных стратегий. Аналогично получаем отрезок .

у

Ломанная - верхняя цена игры. ММ₁-цена игры.