§3. Игра двух сторон с нулевой суммой.

Исходные данные игры двух сторон с нулевой суммой задаются в виде матрицы выигрышей или платежной матрицей, все элементы которой положительны. Любую матрицу выигрышей, содержащую отрицательные элементы всегда можно преобразовать в матрицу с положительными элементами, если ко всем элементам прибавить соответствующее положительное число. И, чтобы это число не влияло на величину выигрыша после решения и получения выигрыша из него вычитывают это положительное число.

Задача. Пусть дана матрица игры

						Наименьший выигрыш игрока А
		45	40	15	20	15
		50	35	6	25	6
		40	30	25	70	25
Наибольший проигрыш игрока В		50	40	25	70

В данной задаче игрок А имеет три чистые стратегии . Игрок В имеет четыре чистых стратегии . Сторона А не знает как поступит сторона В, однако, действуя целесообразно, она выбирает стратегию , которая гарантирует ей наибольший (25) из трех возможных наименьших выигрышей (15,6,25).

Такой подход игрока А называют максиминного выигрыша, т.е.

.

Определяемая таким образом величина α называется нижней ценой игры, максиминным выигрышем, или сокращенно максимином.

Если рассуждать аналогично, сторона В выберет стратегию , которая гарантирует ей наименьший (25) из четырех возможных наибольших проигрышей (50,40,25,70). Принято говорить, что сторона В руководствуется принципом минимаксного проигрыша:

.

Величина β называется верхней ценой игры, или минимаксом.

Принцип, который определяет выбор сторонами стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, называют принципом минимакса или принципом разумной осторожности.

Если стороны А и В будут использовать принцип минимакса, то выигрыш стороны А составит .

В нашем случае нижняя цена игры α равна верхней цене игры β. Это значит, что решение игры находится в области чистых стратегий.

Если цена игры V=α=β, то точка, в которой это совпадение произошло, называется седловой точкой платежной матрицы. Отклонение от этой точки любой из сторон приводит к уменьшению выигрыша.

Можно сформулировать рациональные правила поведения стороны А.

1. Если известна стратегия стороны В, например, , то игрок А должен выбрать ту из своих стратегий , которая обеспечивает ей максимальный выигрыш , тогда цена игры V=50.

2. Если стратегия игрока В неизвестна, то игрок А должен воспользоваться своей максимальной стратегией, которая обеспечивает ему в самых неблагоприятных условиях максимально возможный выигрыш V=25.

3. Если стратегия стороны В неизвестна и состязательная игра имеет седловую точку, то наиболее выгодно обоим игрокам не отклоняться от своих оптимальных стратегий, соответствующих седловой точке.

Пусть теперь платежная матрица не имеет седловой точки, т.е. α≠β. Тогда для определения успеха необходимо выбрать стратегии игроков А и В с определенными вероятностями или частотами многократной игры.

Такие стратегии называют смешанными. В таких играх ход любого игрока остается непредсказуемым, но вся совокупность ходов обладает вполне определенными, заранее заданными свойствами, т.е. участники конфликта чередуют в случайном порядке свои стратегии в соответствии со специально разработанной схемой, обеспечивающей нужную вероятность реализации каждой из стратегий . Если обозначить через вероятность выбора игроком А своей i-й стратегии , то можно говорить о распределении вероятностей, т.е.

А			…
p			…

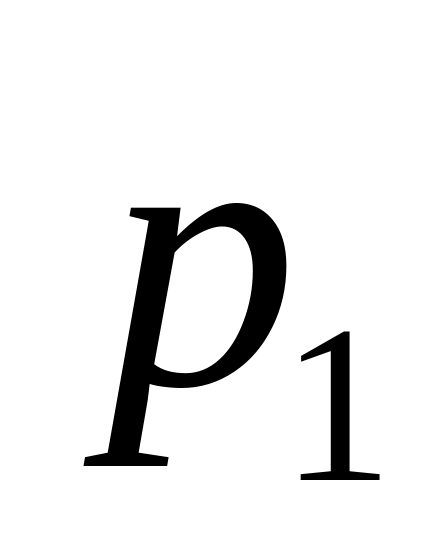
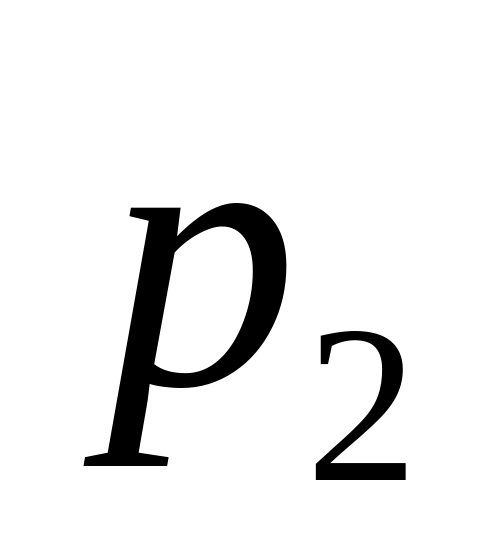
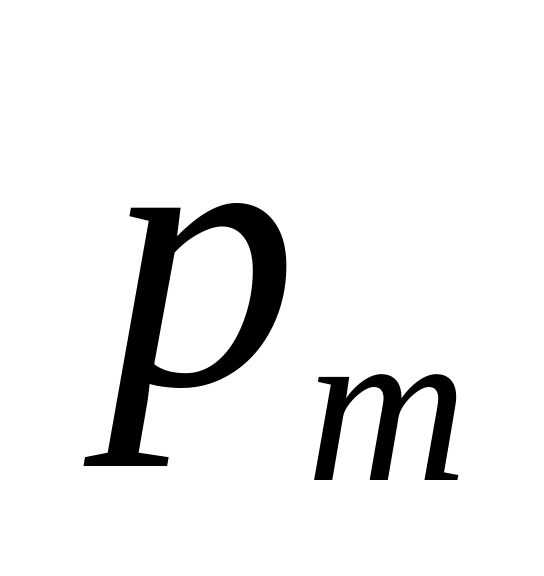
где и , т.е. - вероятности использования соответствующих чистых стратегий в игре

.

Смешанная стратегия, гарантирующая данному игроку А наибольший возможный выигрыш независимо от действий другого игрока В называется оптимальной стратегией первого игрока.

Аналогично можно определить оптимальную стратегию для второго игрока В. Если через обозначить вероятности того, что второй игрок В будет пользоваться своими чистыми стратегиями, то получим распределение вероятностей для второго игрока В:

В			…
q			…

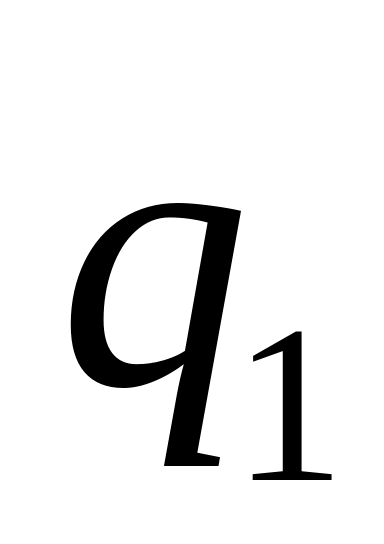
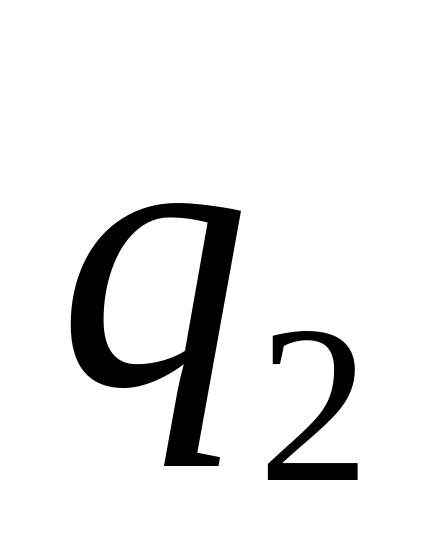
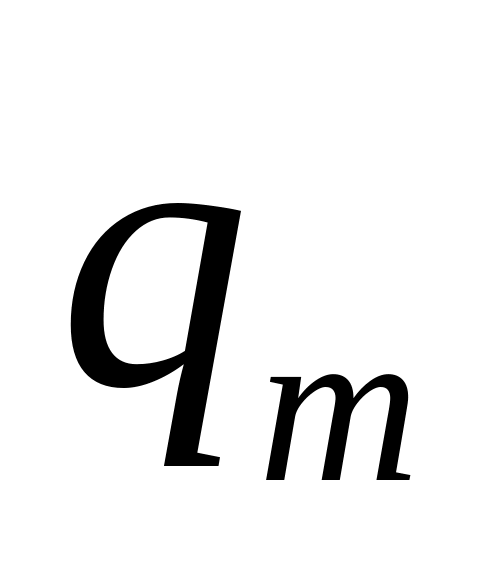
где и .

Смешанная стратегия, которая гарантирует второму игроку наименьший проигрыш независимо от действия первого игрока А называется оптимальной стратегией второго игрока В.

В результате такой игры, т.е. и первый и второй игроки применяют свои смешанные стратегии, цена игры будет равна математическому ожиданию

.

Как уже было сказано, если α=β, то у игры есть седловая точка, в которой наступает равновесие. Если α≠β, то цена игры V находится между нижней и верхней ценой игры, т.е.

α<V<β.

Если пользоваться смешанной стратегией, то получится улучшение игры в среднем для обоих участников игры, так как

и .

Другими словами, первый игрок, пользуясь смешанной стратегией, может только увеличить свой выигрыш , а второй игрок уменьшить свой проигрыш . Возникает вопрос о том, связаны ли между собой величины и . Ответ на этот вопрос дает теорема о минимаксе. Эта теорема указывает на существования равновесия и для случая α≠β, и, следовательно, существуют оптимальные стратегии и .

Пусть игра не имеет седловую точку. Требуется найти ее решение и .

Теорема (Дж.Нейман).

Любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение – пара смешанных стратегий и соответствующую цену игры V.

Доказательство. Эта пара оптимальных стратегий обладает свойством: если один из игроков придерживается своей оптимальной стратегии другому не выгодно отступать от своей оптимальной и ожидаемый выигрыш останется неизменным и равным цене игры V независимо от характера действия другого участника, если он действует в пределах своих активных стратегий.

Пусть оптимальная стратегия состоит из активных стратегий с соответствующими вероятностями . Для остальных стратегий вероятности равны нулю, поэтому .

Пусть теперь оптимальные стратегии игрока В состоят из с вероятностями и .

Предположим, что игрок А придерживается своей оптимальной стратегии , а игрок В пользуется чистыми активными стратегиями поочередно. Обозначим эти выигрыши игрока А через . Так как игроку В не выгодно любое отклонение от своей оптимальной стратегии, то

, (1)

где .

Выразим выигрыш V при оптимальных стратегиях и через .

Так как при стратегии игрока А игрок В применяет свои стратегии с частотой , то

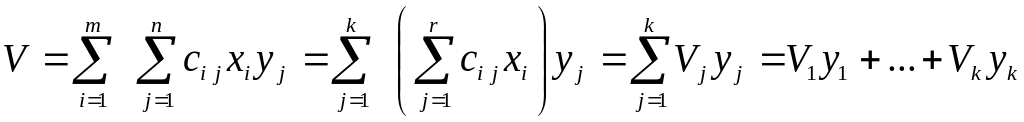. (2)

Если в неравенствах (1) хотя бы в одном месте будет стоять знак строгого неравенства, то получим

,

что противоречит условию (2). Следовательно, в не строгих неравенствах (1) стоят знаки равенства.

Пусть теперь игрок А придерживается оптимальной стратегии , а игрок В выбирает свои активные стратегии с произвольными частотами , для которых

.

Тогда с учетом равенств

Получим

.

Эта теорема позволяет найти цену игры при использовании своих оптимальных смешанных стратегий обоими игроками А и В.

При и

(3)

При ограничениях

(4)

(5)

(6)

Для получения оптимальных вероятностей использования чистых стратегий и необходимо взять соответствующие частные производные от целевой функции V, приравнять их нулю и решить систему уравнений

Таким образом, получается задача математического программирования с целевой функцией (3) и с ограничениями (4), (5) и (6).

Пример. Исследовать матрицу игры 2×2

и определить оптимальные смешанные стратегии.

Решение. Обозначим через - оптимальное значение вероятности того, что первый игрок А воспользуется своей чистой первой стратегией , т.е. .

Аналогично ,

вероятность того, что игрок А воспользуется своей второй стратегией.

Точно также определяются оптимальные вероятности и того, что второй игрок В воспользуется своими стратегиями соответственно, т.е.

и .

Так как у обоих игроков только по две стратегии, то

и .

Таким образом, мы можем считать стратегии игроков случайными величинами и записать их в виде

и .

Тогда цена игры будет равняться математическому ожиданию двумерных независимых величин

(7)

Это есть целевая функция, оптимальное значение максимум которой надо найти.

Ограничения

(8)

(9)

Получили математическую модель (7)-(9).

Решим эту задачу. Для этого обозначим , а , аналогично , а .

Тогда целевая функция примет вид

.

Найдем частные производные по p и q и приравняем нулю:

Решая эту систему, получим

и . (10)

При этом должны выполняться необходимые условия

Значения и , меньшие нуля, необходимо считать равными нулю, а большие единицы – равными единице.

Используя равенства (10) получим

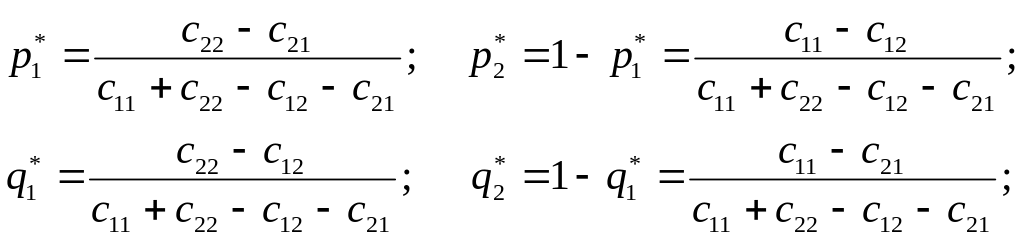(11)

При таких значениях целевая функция (7) примет значение:

(12)

Если проанализируем полученную формулу, то видим, что при

или

игра становится безобидной.

Эти же самые формулы (11) и (12) можно получить, пользуясь теоремой Неймана, с учетом договоренности о том, что первый игрок стремится как можно больше выиграть, а второй как можно меньше проиграть.

Действительно, пусть дана матрица игры 2×2

.

Предположим, что у этой матрицы нет седловой точки, т.е. α≠β. Тогда решение игры ищем в смешанных стратегиях

и ,

где соответствующие вероятности выбора чистых стратегий обоими игроками и .

Согласно основной теореме теории игр, применение оптимальной стратегии обеспечивает первому игроку А выигрыш V при любой стратегии игрока В, поэтому для получения аналитических формул для нахождения и предположим, что первый игрок А пользуется своей оптимальной стратегией , а второй игрок В сначала пользуется своей чистой стратегией , тогда получим

затем первый игрок А продолжает пользоваться своей оптимальной стратегией , а второй игрок применяет свою вторую чистую стратегию , тогда получим

.

Но с другой стороны имеем , поэтому получаем систему трех уравнений с тремя неизвестными

Решая эту систему, получим

(13)

Аналогично рассуждая по отношению уже игрока В, когда он пользуется каждый раз своей оптимальной стратегией , а первый поочередно пользуется своими чистыми стратегиями, получим (14)

Сравнивая формулы (13) и (14) с формулами (11) и (12) видим, что они совпадают.

Пример. Найти оптимальное решение и цену игры для платежной матрицы

.

Решение. Сначала проверим, есть ли у этой игры седловая точка

α=max(-3;-2)=-2; β=min(4;5)=4.

α≠β, следовательно, нет седловой точки и цена игры не определена так как

Решение ищем в смешанных стратегиях: и . Но, сначала получим матрицу игры с положительными элементами. Для этого ко всем элементам матрицы А прибавим число 4, получим:

.

От этого решение игры не изменится, а только цена игры увеличится на 4.

Воспользуемся формулами (13) и (14), получим

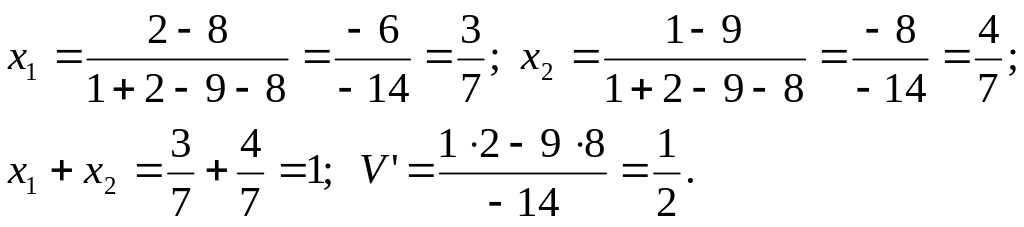
Аналогично

Решение исходной игры:

; .

При таком решении игры цена исходной игры