§2. Классификация игр.

Игры можно классифицировать следующим образом:

1. По стратегии принимаемых решений с чистыми и смешанными стратегиями.

Если игроки применяют в своих действиях одну возможную стратегию из некоторого конечного числа стратегий, то такие задачи называют задачами с чистыми стратегиями.

Если стороны применяют две или более чистых стратегий с вероятностями меньшими 1, то такие задачи считаются задачами со смешанными стратегиями;

2. По количеству возможных стратегий игры делятся на конечные и бесконечные.

Если в игре есть возможность перебрать все возможные стратегии сторон и составить матрицу выигрышей, то задача считается с конечным числом стратегий, и записывается так:

где - выигрыш стороны А, если она выбрала стратегию i, а сторона В выбрала стратегию j. Такие задачи называют матричными играми.

Если в игре невозможно перебрать всевозможные стратегии и их комбинации, то такие задачи называют бесконечными;

3. По количественному результату игры могут быть с нулевой и ненулевой суммами.

Если в игре сумма выигрышей всех игроков равна нулю, то такие задачи называют играми с нулевой суммой. В таких играх, если участвуют две стороны, то проигрыш одной стороны равен выигрышу другой.

Самый простой случай – парная игра двух лиц с нулевой суммой – называется антагонистической или игрой со строгим соперничеством.

Игра двухходовая. А именно, игрок А выбирает одну из своих возможных стратегий , а игрок В выбирает свою стратегию, причем каждый выбор производится при полном незнании выбора другого игрока. Тогда выигрыш удовлетворяет уравнению

где решение игры в чистых стратегиях, и - величины выигрышей соответствующих игроков.

Если обозначить

то

.

Например, пусть дана матрица игры

.

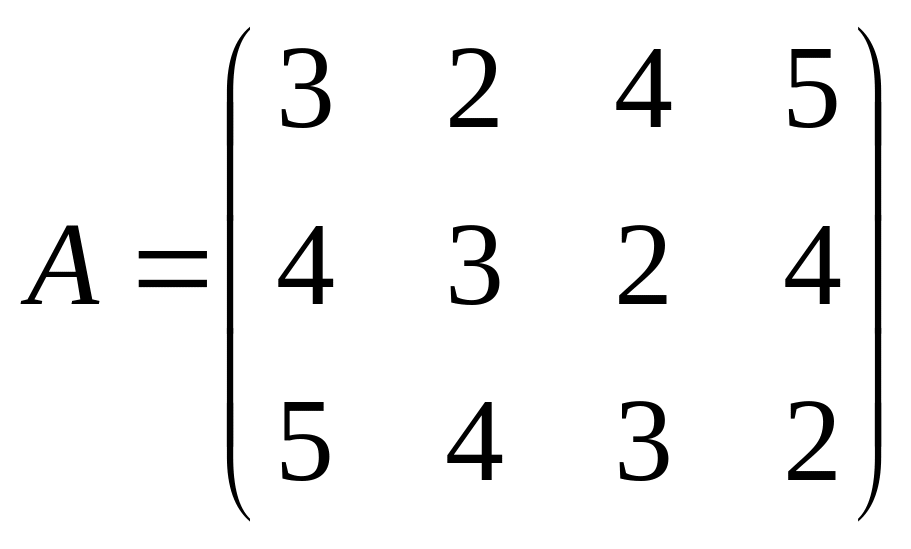Если первый игрок А выбирает свою чистую стратегию , а игрок В свою чистую стратегию , то такому решению игры соответствует выигрыш .

Это число соответствует пересечению второй строки и четвертого столбца. Полученный результат означает, что первый игрок выиграет 4 единицы, а второй проиграет эти же четыре единицы.

При такой постановке задачи цель игрока А максимизировать функцию , а игрока В – минимизировать эту функцию. Влияние стратегии на величину является неопределенным. Определенность наступает после выбора игроком В некоторой стратегии ;

4. По характеру взаимоотношений игроков игры делятся на некооперативные и кооперативные.

Некооперативными считаются те игры, в которых не допускается никакой связи между сторонами, т.е. стороны не могут составлять коалиции с целью применения согласованной стратегии. В этом случае интересы сторон антагонистические. Если стороны могут составлять коалицию, то такие игры считаются кооперативными;

5. По количеству участников делятся на игры двух сторон и многих сторон;

6. По характеру протекания конфликта игры делятся на непрерывные и дискретные.

Если множество стратегий сторон является замкнутым числовым интервалом, то получается состязательная игра с непрерывным протеканием конфликта, в противном случае – дискретным. Изучению моделей таких конфликтов посвящены два практически самостоятельных направления в теории игр: дифференциальные и многошаговые игры.

Дифференциальной называют игру, в которой стороны выбирают решения в каждый момент, а состояние игры описывается дифференциальными уравнениями, в которые выбранные значения стратегий сторон входят в качестве уравнений. В дальнейшем ограничимся рассмотрением многошаговых игр;

7. По количеству имеющейся у сторон информации:

– с полной информацией. Каждой стороне точно известно, как будет поступать другая сторона, результаты своих действий, а также состояние игры на предыдущих шагах, если игра многошаговая;

– с неполной информацией, если стороны имеют лишь вероятностную информацию об игре: о функциях выигрыша, о стратегиях сторон, об относительной осведомленности сторон о различных сторонах игры и т.д.;

– неопределенные, если стороны не имеют даже вероятностной информации об игре.