
3.2.2. Интегральная формула Коши.
Теорема
3. Пусть
голоморфна в области G и
Г – спрямляемая жорданова замкнутая
кривая, целиком лежащая в G,
тогда
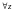 ,
лежащего внутри кривой Г:
,
лежащего внутри кривой Г:
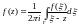 (1)
(1)
Формула (1) называется интегральной формулой Коши.
Рассмотрим функцию
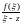 по переменной
по переменной
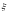 (z – фиксированная точка
лежащая внутри r ). Она
аналитична в G\{z}.
Рассмотрим круг
(z – фиксированная точка
лежащая внутри r ). Она
аналитична в G\{z}.
Рассмотрим круг
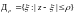 и выберем
и выберем
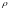 настолько малым, что бы этот круг
находился внутри Г. Рассмотрим двусвязную
область с контуром
настолько малым, что бы этот круг
находился внутри Г. Рассмотрим двусвязную
область с контуром
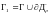 .
Для данной функции применим следствие
из теоремы Коши. Тогда
.
Для данной функции применим следствие
из теоремы Коши. Тогда
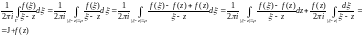 Поскольку
аналитична в точке z, а
следовательно и непрерывна в ней, то
Поскольку
аналитична в точке z, а
следовательно и непрерывна в ней, то
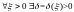 ,
такое что при
,
такое что при
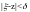 имеем
имеем
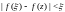 .
Выберем
.
Выберем
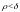 ,
тогда
,
тогда
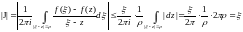 .
Но, как легко видеть , J –
не зависит от
,
.
Но, как легко видеть , J –
не зависит от
,
Поэтому
последнее неравенство при любом
 возьмем лишь если J=0
возьмем лишь если J=0
Используя ИОТК можно доказать следующую теорему:
Теорема
4. Пусть функция
аналитична в области G и
непрерывна в
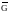 ,
тогда
,
тогда
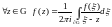 (2)
(2)
G – односвязная область, ограниченная спрямляемой жордановой кривой.
Замечание 1. Интегральные формулы Коши (1) и (2) являются основными формулами в теории аналитических функций.
Замечание
2. Если область G является
многосвязной, и Г – ее граница, то
переходя к односвязной области
и дословно повторяя рассуждения,
проводимые с
выше, получим:
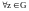
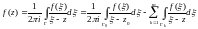 (3).
(3).
4.1.4 Теорема Лиувилля о нулях аналитической функции.
Определение: Точка в которой аналитическая функция обращается в нуль, называется нулем аналитической функции.
Теорема: Всякая функция аналитическая в области G и отличная от константы, может иметь в этой области не более чем счетное число нулей.
В силу теоремы единственности нули
аналитической функции не могут иметь
предельных точек внутри области G
(в противном случае
 ).
Нули могут иметь предельную точку лишь
на
).
Нули могут иметь предельную точку лишь
на
 .
Рассмотрим области
.
Рассмотрим области
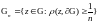 .
В силу предыдущего рассуждений
.
В силу предыдущего рассуждений
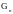 имеется лишь конечное число нулей. Их
множество обозначим через
имеется лишь конечное число нулей. Их
множество обозначим через
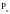 .
Тогда множество P всех
нулей функции
.
Тогда множество P всех
нулей функции
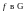
равно
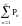 .
Последнее множество счетно.
.
Последнее множество счетно.
Определение: Если разложение аналитической функции в некоторой точке z=b отсутствуют первые m членов, т.е. разложение начинается с m-ой степени z-b, то говорят что точка z=b является нулем функции порядка m .
Теорема.
Пусть
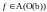 .
Тогда (z=b –
нуль кратности m )
.
Тогда (z=b –
нуль кратности m )
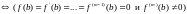 .
.
Доказательство вытекает из того, что
степенной ряд для
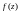 есть
ее ряд Тейлора и, следовательно
есть
ее ряд Тейлора и, следовательно
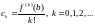 .
Но тогда
.
Но тогда
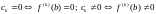
ЛЕММА. (Неравенство Коши для коэффициентов Тейлора).
Пусть
S(z) – сумма
степенного ряда
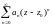 ,
радиус сходимости которого равен R>0.
Тогда для коэффициентов Тейлора этого
ряда имеет место неравенство: Если М>0
– такое число, что
,
радиус сходимости которого равен R>0.
Тогда для коэффициентов Тейлора этого
ряда имеет место неравенство: Если М>0
– такое число, что
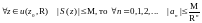 .
.
По формуле для коэффициентов Тейлора имеем:
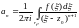 ,
где
,
где
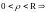
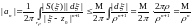 .
Переходя к примеру при
.
Переходя к примеру при
 ,
получим неравенство Коши.
,
получим неравенство Коши.
Воспользуемся этой леммой для доказательства следующей теоремы Лиувилля.
Теоремы. Если некоторая функция аналитична во всей комплексной плоскости и ограничена на по модулю, то она есть постоянная функция.
Рассмотрим
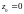 и
разложим
в окрестности этой точки в ряд Тейлора:
и
разложим
в окрестности этой точки в ряд Тейлора:
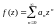
В
силу условия теоремы оценка для
коэффициентов
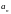 справедлива при любых
справедлива при любых
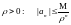
Переходя
при n=1,2,… к пределу при
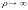 ,
получаем, что
,
получаем, что
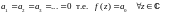
Теорема (об аналитичности суммы
степенного ряда). В круге сходимости
{z| |z|<R}
степенного ряда
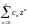 (1),
его сумма S(z)
является голоморфной функцией. При этом
производную функции S
можно вычислить почленным дифференцированием
ряда(1), т.е.
(1),
его сумма S(z)
является голоморфной функцией. При этом
производную функции S
можно вычислить почленным дифференцированием
ряда(1), т.е.
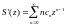 (2)
(2)
Замечание об аналитичности суммы
ряда:
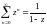 .
Сумма этого ряда определена в круге {z:
|z|<1}, а
.
Сумма этого ряда определена в круге {z:
|z|<1}, а
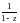 аналитична
также и всюду, кроме точки z=1.
аналитична
также и всюду, кроме точки z=1.
Доказательство теоремы:
1. Покажем, что радиус сходимости ряда(2)
совпадает с радиусом сходимости ряда(1)
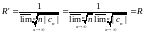 .
.
2. Далее, покажем, что S(z) является дифференцируемой.
Пусть
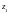 - произвольная точка из круга сходимости,
тогда существует точка
- произвольная точка из круга сходимости,
тогда существует точка
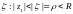 .
Поскольку при
.
Поскольку при
 ряд(2) сходится абсолютно, то ряд
ряд(2) сходится абсолютно, то ряд
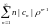 сходится. Следовательно
сходится. Следовательно
 остаток
ряда удовлетворяет неравенству
остаток
ряда удовлетворяет неравенству
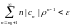 (3).
Тогда
(3).
Тогда
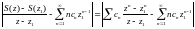 =
=
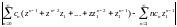
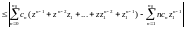 +
+
Из неравенства(3) следует, что
последовательность сл.
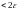 ,
а выражение, стоящее под знаком модуля,
является непрерывной функцией и при
,
а выражение, стоящее под знаком модуля,
является непрерывной функцией и при
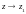 стремящейся к 0. Поэтому
стремящейся к 0. Поэтому
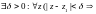 нерв.
сл.
нерв.
сл.
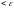 )…
)…
Замечание для ряда(2) также выполняются
все условия данной теоремы, поэтому
применяя теорему к функции S’(z)
получаем, что
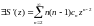 и
т.д.
и
т.д.
Т.о., сумма степенного ряда является функцией бесконечно дифференцируемой в круге сходимости и при этом -я производная этой функции находится путем -кратного дифференцирования ряда(1).
Теорема
(теорема Лорана) Пусть функция
аналитична
в кольце
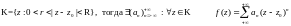 (4)
(4)
Ряд
(4) называется рядом Лорана, а разложение
(4) – разложением Лорана: При этом
,
где n=…,-1,0,1,…, a
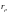 -
произвольная окружность с центром в
точке
-
произвольная окружность с центром в
точке
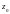 ,
лежащая в кольце
,
лежащая в кольце
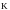 .
.
Рассмотрим
кольцо
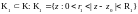 ,
где
,
где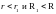 .
К этому кольцу применим ИТК для двусвязной
области. Тогда ,
.
К этому кольцу применим ИТК для двусвязной
области. Тогда ,
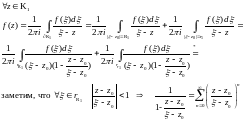
которое
равномерно сходится по
.
Аналогично,
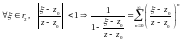 .
С учетом данных разложений, а так же
возможности почленно интегрировать
равномерно сходящийся ряд получаем:
.
С учетом данных разложений, а так же
возможности почленно интегрировать
равномерно сходящийся ряд получаем:
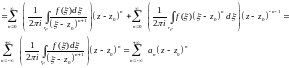
По
пути был осуществлен переход от
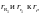 это позволяет сделать ИТК.
это позволяет сделать ИТК.
Замечание.
Перепишем ряд (4) в следующем виде:
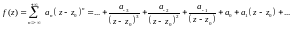
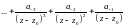 -
-
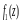 -главная часть ряда Лорана
-главная часть ряда Лорана
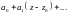 -
-
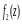 - правильная часть ряда Лорана
- правильная часть ряда Лорана
Если главная часть отсутствует, то ряд Лорана превращается в ряд Тейлора функции , при этом будет аналитична не только в кольце, но и в круге.
5.1.2.Основная теорема о вычетах.
Теорема 1. Пусть f
аналитична в замкнутой односвязной
области
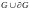 со спрямляемой границей за исключением
конечного числа изолированных особых
точек
со спрямляемой границей за исключением
конечного числа изолированных особых
точек
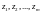 ,
целиком лежащих в G, тогда:
,
целиком лежащих в G, тогда:
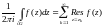 (1).
(1).
Т.к.
G – открытое множество,
то
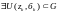 .
.
Обозначим
через
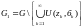 .
В области
.
В области
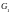 функция
является аналитической, тогда по
интегральной теореме Коши для много
связной области имеем:
функция
является аналитической, тогда по
интегральной теореме Коши для много
связной области имеем:
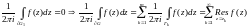
Следствие. Пусть
в расширенной комплексной плоскости
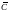 имеет конечное число изолированных
особых точек(
имеет конечное число изолированных
особых точек(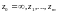 ).
Тогда
).
Тогда
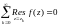 .
.
Выберем
центром в точке О и со столь большим
радиусом, чтобы все конечные изолированные
точки оказались внутри нее. Тогда
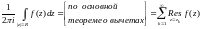 .
.
С
другой стороны, вычет
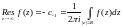 .
Складывая обе части равенства, имеем:
.
.
Складывая обе части равенства, имеем:
.
