2. Общие комплексные сопротивления и проводимости цепей синусоидального тока.

Z = ;

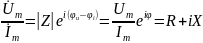где: его модуль – ; ;

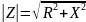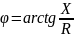полная комплексная проводимость (Y):

;

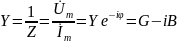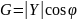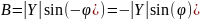где - резистивная часть комплексной проводимости; – реактивная часть комплексной проводимост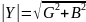и.

и .

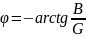3. Свойства передаточной функции. Формула обращения.

_p: k(iw)=k(p).Эта ф-ия яв. Аналитической во всей плоскости комплексной частоты p за исключением точек являющихся корнями знаменателя

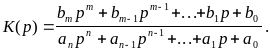
_{и эти точки наз. полюсами. передаточная ф-ия в нуль-полюсном представлении:}

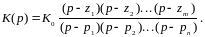
5 Билет

1. Свойства параметрических и нелинейных цепей. Этапы анализа цепей.

Линейная цепь с переменными параметрами (R,L,C)=F(t)

Основные свойства:

1) операции умножения , дифференц., интегрироваия являются линейными.

2)независимость соотношения между входными и выходными напряжениями (токами) от уровня входного напряжения (тока);

3) принципа независимости (суперпозиции = наложения): при воздействии на линейную цепь нескольких внешних сил поведение цепи (ток, напряжение) можно определять путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности; e(t)= E₀ cos(w₀ t + ₀);

Нелинейная цепь (R,L,C)=F(t, U(t),i(t));

Основные свойства:

1) операции умножения , дифференц., интегрироваия являются линейными.

2)независимость соотношения между входными и выходными напряжениями (токами) от уровня входного напряжения (тока);

3) принципа независимости (суперпозиции = наложения): при воздействии на линейную цепь нескольких внешних сил поведение цепи (ток, напряжение) можно определять путем наложения решений, найденных для каждой из сил в отдельности;

Не выполняются

Этапы анализа цепей:

1)Составление математической модели исследуемой цепи.

2)Составление дифференциальных уравнений математической модели и их решение.

3)Исследование полученных решений и определение характеристик исследуемой цепи.

4)Проведение эксперимента и сравнение экспериментальных результатов с теоретическими;

2. Последовательное соединение элементов цепи синусоидального тока.

п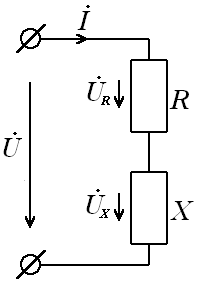 о второму закону Кирхгофа для данной схемы можем записать:

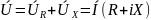, где .

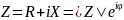Если в качестве реактивного сопротивления будет сопротивление катушки 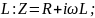где 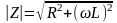; 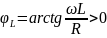.Для цепи с емкостным элементом тогда

; .

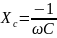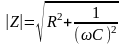
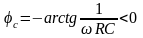Т. О., для последовательного соединения резистора и конденсатора фаза или аргумент полного комплексного сопротивления является величиной отрицательной.

Для проводимостей реактивных элементов сдвиг фаз между током и напряжением будет иметь соответственно противоположные (обратные) знаки.

3. Аналитические свойства входного сопротивления двухполюсника.

Теория цепей делится на 2е основные части - анализ и синтез. Задача анализа – нахождение внешних хар-к системы, структура которой задана заранее в виде принципиальной схемы. Задача синтеза по исходной внешней хар-ке, как правило ЧКП необходимо определить оптимальную структуру цепи, реализующей данную хар-ку.

Для 2х-полюсников основной исходной хар-кой для синтеза является ф-ия вх. сопротивления,которая обозначается- Z(p): Z(p) = U(p) / I(p)-вх. проводимость,Y(p)=I(p)/U(p)

_Ф-ия Z(p) определена во всей плоскости Z(p) и также как и передаточная ф-ия может быть записана в виде: