25 Билет

1. Эквивалентные преобразования линейных электрических цепей.

основные эквивалентные преобразования:

1. РИН ↔РИТ.

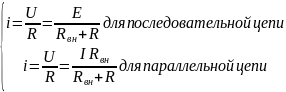
условие эквивалентности: .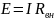

При этом идеальные источники напряжения и тока не взаимозаменяемы.

2. Замена нескольких последовательно соединённых элементов одним эквивалентным:

При этом 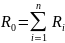, где .

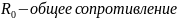3. Замена нескольких параллельно соединённых сопротивлений (проводимостей) одним эквивалентным:

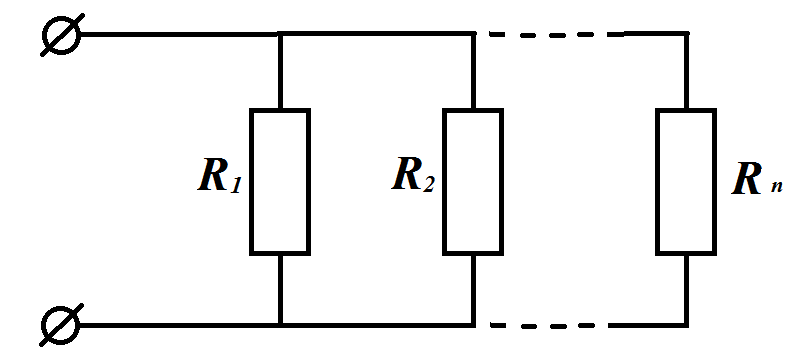
При этом .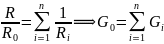

4. Замена нескольких последовательно соединённых источников напряжения (РИН) и их внутренних сопротивлений:

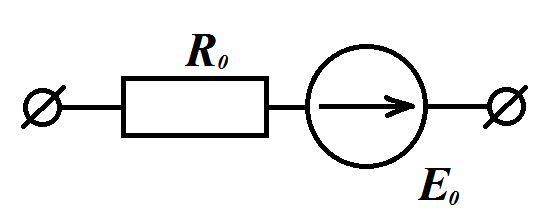
При этом эквивалентные значения будут равны сумме (с учетом направлений ЭДС):

.

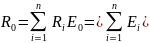5. Замена параллельного соединения нескольких источников тока (РИТ) и их проводимостей одним эквивалентным:

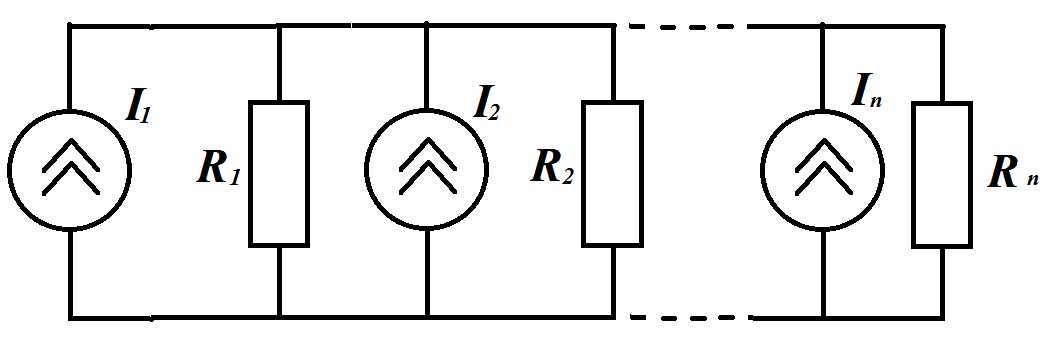
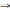
Результирующие значения также будут суммироваться с учетом направлений токов:

.

6. Замена нескольких параллельно соединённых реальных источников напряжения одним эквивалентным источником тока.

7. Замена нескольких последовательно соединённых реальных источников тока одним эквивалентным РИН.

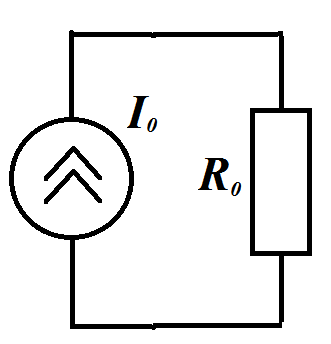
8. Взаимные преобразования треугольника и звезды:

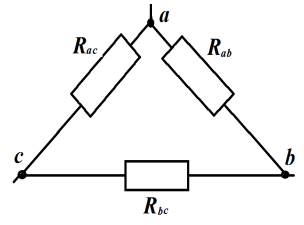
При этом: ; ; ;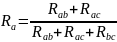

И ; ; .

Если в узлах «звезды» , то в ветвях «треугольника»:

2. Импульсная характеристика линейной стационарной системы. Интеграл Дюамеля.

импульсной характеристикой системы называется функция h(t), являющаяся откликом системы на входной сигнал вида (t), т.е. h(t) удовлетворяет следующему уравнению:

h(t) = T (t).

при смещении входного воздействия во времени на t₀:

h(t - t₀) = T (t - t₀).

C физической точки зрения импульсная характеристика приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временем установления стационарного состояния системы.

Интеграл Дюамеля. В силу фильтрующего свойства дельта-функции сигнал всегда может быть представлен следующим образом: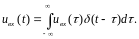 Тогда отвечающая ему выходная реакция: интеграл Дюамеля и является основной формулой временного метода анализа систем.

Парциальные импульсные характеристики h_ij(t) (i = 1,2, .., n; j = 1,2, .., m), каждая из которых отображает сигнал на i-ом выходе при подаче на j-ый вход дельта-функции. Совокупность функций h_ij(t) образует матрицу импульсных характеристик:

Формула интеграла Дюамеля в многомерном случае приобретает вид: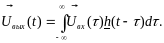 где U_вых(t) – n-мерный вектор, U_вх(t) – m-мерный вектор.

Условие физической реализуемости. Для любых видов импульсных характеристик физически реализуемых систем всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до момента подачи сигнала на вход. Изложенный принцип накладывает очень простое ограничение на вид допустимых импульсных характеристик: h(t) = 0 при t < 0.

Для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменен на текущее значение времени: физический смысл: линейная стационарная система производит операцию взвешенного суммирования всех мгновенных значений сигнала, поступивших на вход и существовавших «в прошлом» при - <  < t. Роль весовой функции при этом выполняет импульсная характеристика системы. Принципиально важно, что физически реализуемая система ни при каких обстоятельствах не способна оперировать с информацией, заключенной в «будущих» значениях сигнала.