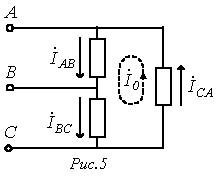
2. Свойства симметричных составляющих токов, напряжений и сопротивлений различных последовательностей трехфазных систем.

Рассмотрим четырехпроводную систему. Для тока в нейтральном п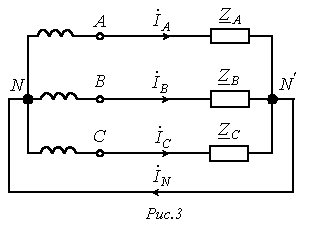 роводе имеем

.

ток в нейтральном проводе равен утроенному току нулевой последовательности. Если нейтрального провода нет, то   нет составляющих тока нулевой последовательности.

Р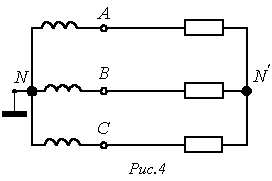 ассмотрим трехпроводную несимметричную систему .

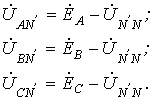
просуммировав эти соотношения, для симметричных составляющих нулевой последовательности фазных напряжений можно записать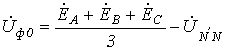 .Если система ЭДС генератора симметрична, то из последнего получаем

• в фазных напряжениях симметричного приемника отсутствуют симметричные составляющие нулевой последовательности;

• симметричные составляющие нулевой последовательности фазных напряжений несимметричного приемника определяются величиной напряжения смещения нейтрали;

• фазные напряжения несимметричных приемников, соединенных звездой, при питании от одного источника различаются только за счет симметричных составляющих нулевой п оследовательности.

Сопротивления симметричной трехфазной цепи для токов различных последовательностей

Если к симметричной цепи приложена симметричная система фазных напряжений прямой (обратной или нулевой) последовательностей, то в ней возникает симметричная система токов прямой (обратной или нулевой) последовательности. При использовании метода симметричных составляющих симметричные составляющие напряжений связаны с симметричными составляющими токов той же последовательности. 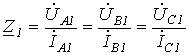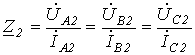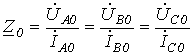Отношение симметричных составляющих фазных напряжений прямой (обратной или нулевой) последовательности к соответствующим симметричным составляющим токов называется комплексным сопротивлением прямой ,обратной и нулевой последовательностей.

3. Устойчивость цепей с ос.

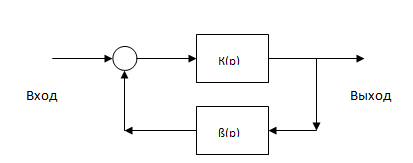
Рассмотрим систему с обратной связью с передаточной функцией К(р) и звеном обратной связи с передаточной функцией ß(р) и внешний входной сигнал не подается, т.е. U_вх(р)=0.Уравнение состояния: U_вых (p) = K(p)ß(p)U_вых(p) (1 - K(p)ß(p)) U_вых(p) = 0.

1 - K(p)ß(p)= 0. Для того, чтобы цепь с ОС была абсолютная устойчива, необходимо, чтобы корни этого уравнения имели отрицательные вещественные части, т.е. располагались в левой полуплоскости комплексной частоты.

Алгебраические критерии устойчивости.

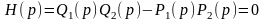Основной элемент и элемент ОС являются цепями с сосредоточенными параметрами и запишем: K(p) = P₁(p)/Q₁(p); ß(p) = P₂(p)/Q₂(p) система с ОС будет устойчива, если все корни уравнения имеют отрицательные вещественные части. Полиномы Н(р) с такими свойствами называют полиномами Гурвица.

Критерий Рауса-Гурвица : чтобы уравнение a_npⁿ + a_n-1p^n-1 + … + a₁p¹ + a₀ = 0 с вещественными коэффициентами имело корни лишь в левой полуплоскости переменной р, необходимо и достаточно, чтобы положительными были:

- коэффициенты a_n , a₀;

- определитель Рауса-Гурвица и все его главные:

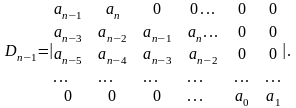
Достоинство критерия Рауса-Гурвица – относительная простота вычислений, Недостаток: применяется только для цепей с сосредоточенными параметрами.

Геометрические (частотные) критерии устойчивости. Произведение w (p) = K(p)ß(p) есть не что иное, как передаточная функция каскадного соединения двух звеньев – основного и звена ОС и называется передаточной функцией системы с разомкнутой ОС и ее можно рассматривать как отображение комплексной плоскости р на другую комплексную плоскость w. При этом корням р₁, р₂, …,р_n характеристического уравнения 1 - K(p)ß(p)= 0 в плоскости w будет соответствовать единственная точка w = 1. возможность самовозбуждения системы с ОС: если образ правой полуплоскости переменной р при отображении на плоскость w содержит точку w = !, то система с замкнутой ОС неустойчива.