2. Метод симметричных составляющих.

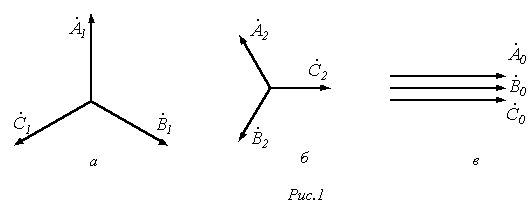
Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими. Различают симметричные составляющие прямой, обратной и нулевой последовательностей, которые различаются порядком чередования фаз.

Симметричную систему прямой последовательности образуют (см. рис. 1,а) три одинаковых по модулю вектора  и  со сдвигом друг по отношению к другу на  рад., причем  отстает от , а  - от .

Введя оператор поворота , для симметричной системы прямой последовательности можно записать .Симметричная система обратной последовательности образована равными по модулю векторами  и  с относительным сдвигом по фазе на  рад., причем теперь  отстает от , а  - от  (см. рис. 1,б). Для этой системы имеем .Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в): .

Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно, ; (1) ;(2) _.(3)

Таким образом, получена система из трех уравнений относительно трех неизвестных , которые, следовательно, определяются однозначно. Для нахождения  сложим уравнения (1)…(3). Тогда, учитывая, что , получим .

Для нахождения  умножим (2) на , а (3) – на , после чего полученные выражения сложим с (1). В результате приходим к соотношению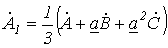 (5) Для определения  с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на  и . В результате имеем: . 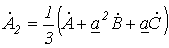(6)

Формулы (1)…(6) справедливы для любой системы векторов , в том числе и для симметричной. В последнем случае .

3. Передаточная функция системы с ос.

Цепи, в которых выходной сигнал или некоторая его часть снова поступает на вход, называются цепями с обратной связью. Введение обратной связи позволяет в ряде случаев существенно улучшить рабочие характеристики цепей.

Рассмотрим линейную систему, состоящую из двух четырехполюсников. Активный 4-полюсник, имеющий передаточную функцию К(р), называется основным элементом системы. Другой, как правило, пассивный 4-полюсник с передаточной функцией ß(р), называется элементом обратной связи. Стрелки указывают направления движения сигналов в системе (рис. 9.1).

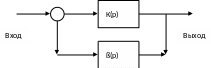
Рис. 9.1 – Линейная система с обратной связью

На входе основного элемента имеется звено, суммирующее входной сигнал и выходную реакцию элемента обратной связи. Тогда соотношение между изображениями входного и выходного сигналов будет следующим: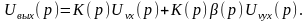 Далее преобразовывая:

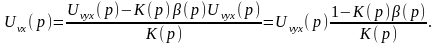
Отсюда можно получить формулу, определяющую передаточную функцию системы с обратной связью: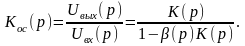

В соответствии с этой формулой, частотные свойства системы в равной мере зависят как от функции К(р), так и от характеристики ß(р) цепи обратной связи. Поэтому можно достаточного широко варьировать частотную характеристику всего устройства, оставляя неизменным основной элемент системы и изменяя лишь параметры элемента обратной связи.

Отрицательная и положительная обратная связь.

Рассмотрим формулу (2) при p = iw. Тогда частотный коэффициент передачи системы с обратной связью запишется следующим образом: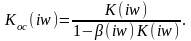 Если на заданной частоте w 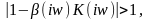то введение обратной связи приведет к уменьшению модуля ЧКП системы и, следовательно, амплитуды выходного сигнала. Такая обратная связь называется отрицательной (ООС). Если имеет место обратное неравенство 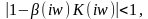то в системе наблюдается положительная обратная связь (ПОС).

Как отрицательная, так и положительная обратные связи широко используются при создании р.т. устройств. Однако следует иметь в виду, что ПОС может явиться причиной неустойчивости системы.

Так, например, если ß(р) является положительной вещественной монотонно возрастающей функцией, то это будет приводить к увеличению коэффициента усиления системы с обратной связью (ЧКП) К_ос до тех пор, пока не выполнится равенство:

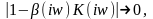или ß = 1/К(р), из которого следует, что К_ос → ∞ и что, следовательно, означает самовозбуждение системы – появление выходного сигнала при отсутствии сигнала на входе.