39. Уравнение Бернулли и метод его решения.

Обыкновенное дифференциальное уравнение вида:

называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение). При является частным случаем уравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году. Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.^[1]

Метод решения

Первый способ

Разделим все члены уравнения на

получим

Делая замену

и дифференцируя, получаем:

Это уравнение приводится к линейному:

и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.

Второй способ

Заменим

тогда:

Подберем так, чтобы было

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения получаем уравнение  — уравнение с разделяющимися переменными.

Пример

Уравнение

разделим на получаем:

Замена переменных

дает:

Умножаем на ,

Результат:

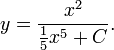
40. Линейные однородные ду второго порядка с постоянными коэффициентами. Теорема о структуре общего решения.

В этой статье мы разберем принципы решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами , где p и q – произвольные действительные числа. Сначала остановимся на теории, далее применим полученные результаты в решении примеров и задач.

Сформулируем теорему, которая указывает, в каком виде находить общее решение ЛОДУ. Общее решение линейного однородного дифференциального уравнения с непрерывными на интервале интегрирования X коэффициентами определяется линейной комбинацией 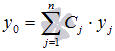, где - линейно независимые частные решения ЛОДУ на X, а - произвольные постоянные. Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид y₀ = C₁ ⋅ y₁ + C₂ ⋅ y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂.

Теорема 1. Если y = y₁ есть решение уравнения (1), то y = c·y₁ является тоже решением уравнение (1), где с — произвольная постоянная.    Доказательство. Так y = y₁ является решением уравнения (1), то

y₁⁽ⁿ⁾ + a₁(x) ·y₁^(n-1) + … + a_n(x) ·y₁ = 0. (2)

Подставляя y = c·y₁ в уравнение (1), получим

(c y₁)⁽ⁿ⁾ + a₁(x) · (c y₁)^(n-1) + … + a_n(x) · (c y₁) = 0.

Воспользовавшись правилами дифференцирования, получим

c·( y₁⁽ⁿ⁾ + a₁(x) ·y₁^(n-1) + … + a_n(x) ·y₁ ) = 0 (3)

в силу свойства (2). Что и требовалось доказать.    Теорема 2. Если y₁ и y₂  является решением уравнения (1) то y = y₁ + y₂ есть тоже решение уравнения (1).    Доказательство. Подставим y = y₁ + y₂ в (1)

(y₁ + y₂)⁽ⁿ⁾ + a₁(x) ·(y₁ + y₂)^(n-1) + … + a_n(x) ·(y₁ + y₂) = 0

Воспользовавшись правилами дифференцирования, получим

(y₁⁽ⁿ⁾ + a₁(x) ·y₁^(n-1) + … + a_n(x) ·y₁) + (y₂⁽ⁿ⁾ + a₁(x) ·y₂^(n-1) + … + a_n(x) ·y₂ ) ≡ 0.

Что и требовалось доказать.