Уравнение первого порядка

Пример

Решение уравнения с начальными условиями Имеем решение в общем виде Решение неопределённого интеграла Можно упростить до где 4/3, после подстановки начальных условий в решение.

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

получим

используем правило дифференцирования произведения

что, после интегрирования обеих частей, дает нам

Таким образом, решение линейного дифференциального уравнения первого порядка

(в частности, с постоянными коэффициентами) имеет вид

где является константой интегрирования.

Пример

Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:

Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер системы.

В этом случае, p(x) = b, r(x) = 1.

Следовательно, решение будет:

34. Решение ду первого порядка с разделяющимися переменными.

Уравнения с разделяющимися переменными

Дифференциальное уравнение называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде . Тогда, в случае , общим решением уравнения является

35. Однородные ду первого порядка, нулевая функция однородности.

О: Функция (х, у) называется однородной функцией го измерения относительно переменных х и у, если при любом X справедливо тождество

Примеры: 1) - однородная функция первого измерения, так как

2) - однородная функция нулевого измерения, так как

О: ОДУ 1-го порядка (20.3) называется однородным относительно х и у, если функция у = есть однородная функция нулевого измерения относительно х и у.

Однородное уравнение может быть записано в виде так как Поэтому заменой

u = у/х, где u = u(х), оно сводится к дифференциальному уравнению с разделяющимися переменными (см. ОК № 20). Пример:

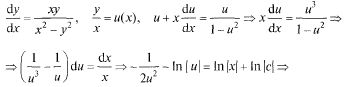
— общий интеграл.

Замечание. Уравнение Р(х, у)dх + Q(x, y)dy = 0 будет однородным только в том случае, если Р(х, у) и Q(x, у) —- однородные функции одного измерения.

36. Решение линейных ду первого порядка. Метод Бернулли.

Метод Бернулли.

 

(Якоб Бернулли (1654-1705) – швейцарский математик.)

 

            Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций  .

            При этом очевидно, что  - дифференцирование по частям.

 

            Подставляя в исходное уравнение, получаем:

            Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

            Например, функция  может быть представлена как

 и т.п.

            Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

            Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

 

 

 

            Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение  с учетом того, что выражение, стоящее в скобках, равно нулю.

 

            Интегрируя, можем найти функцию v:

;             ;

            Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

            Подставляя полученные значения,  получаем:

 

 

            Окончательно получаем формулу:

,     С₂ - произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения  в общем виде по способу Бернулли.