Алгебраическая форма записи комплексного числа, геометрическое изображение.
Алгебраическая форма
Запись
комплексного числа z
в виде
называется алгебраической формой
комплексного числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что
):
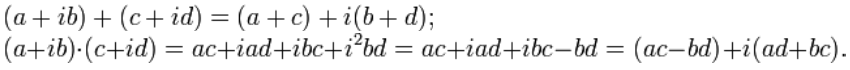
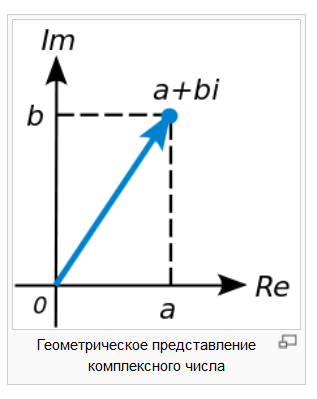
Геометрическое изображение
Рассмотрим
плоскость с прямоугольной системой
координат. Каждому комплексному числу
сопоставим точку плоскости с координатами
(а также радиус-вектор, соединяющий
начало координат с этой точкой). Такая
плоскость называется комплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются соответственно
вещественной и мнимой осями.
Часто бывает удобно рассматривать на комплексной плоскоститакже полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент).
Тригонометрическая и показательная форма записи комплексного числа.
Если
вещественную x
и мнимую y
части комплексного числа выразить
через модуль
и аргумент
то всякое комплексное число z,
кроме нуля, можно записать в
тригонометрической форме
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
где
— расширение экспоненты для случая
комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
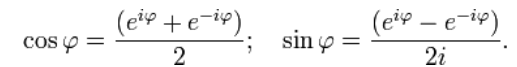
Сложение и вычитание комплексных чисел.
Сумма
двух комплексных числел
есть также комплексное число
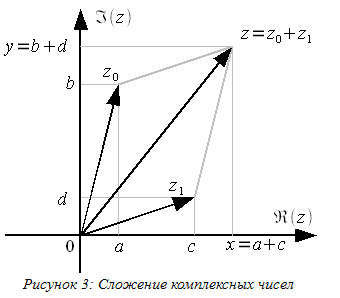
Как следует из выражения (17) при сложении реальные и мнимые части комплексного числа также складываются.
На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3).
Разность
двух комплексных числел
есть также комплексное число
Как следует из выражения (18) при вычитании реальные и мнимые части комплексного числа также вычитаются.
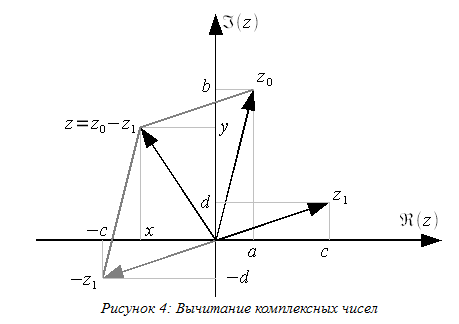
На
комплексной плоскости операцию вычитания
можно реализовать как вычитание векторов
комплексных чисел по правилу параллелограмма
(рисунок 4). На первом шаге из вектора
формиуется вектор
после
чего вектор
складывается с вектором
по правилу параллелограмма.
Умножение и деление комплексных чисел.
Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:
Таким образом получили также комплексное число. Умножать в явном виде комплексные числа не очень удобно, гораздо проще если привести их по формуле Эйлера к показательной форме:
При перемножении в показательной форме модули комплексных числел перемножаются а фазы складываются. На векторной диаграмме это можно представить следующим образом (рисунок 5):
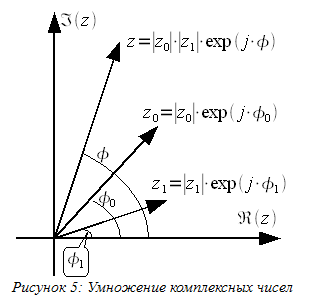
При перемножении результирующий вектор поворачивается и его длина изменяется.
Рассмотрим деление в показательной форме:
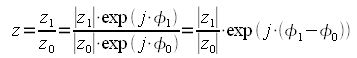
Таким
образом при делении комплексных чисел
их модули делятся а фазы вычитаются.
При делении необходимо чтобы
.
Получим формулу для деления комплексных
чисел в явной форме. Пусть
умножим и числитель и знаменатель дроби на число комплексно-сопряженное знаменателя:
,
Исходя из (22) в знаменателе дроби получим квадрат модуля знаменателя а числитель перемножим по правилу умножения комплексных чисел:
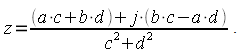
Поделив почленно реальную и мнимую часть числителя на знаменатель получим:
Выражение (27) - формула деления комплексных чисел в явной форме. Как можно заметить операции сложения и вычитания удобнее выполнять в явном виде, тогда как умножать и делить комплексные числа быстрее и легче в показательной форме.
Возведение комплексного числа в натуральную степень, извлечение корня из комплексного числа.
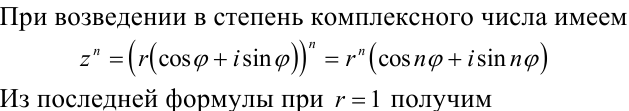
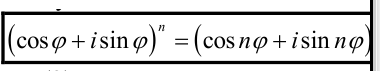
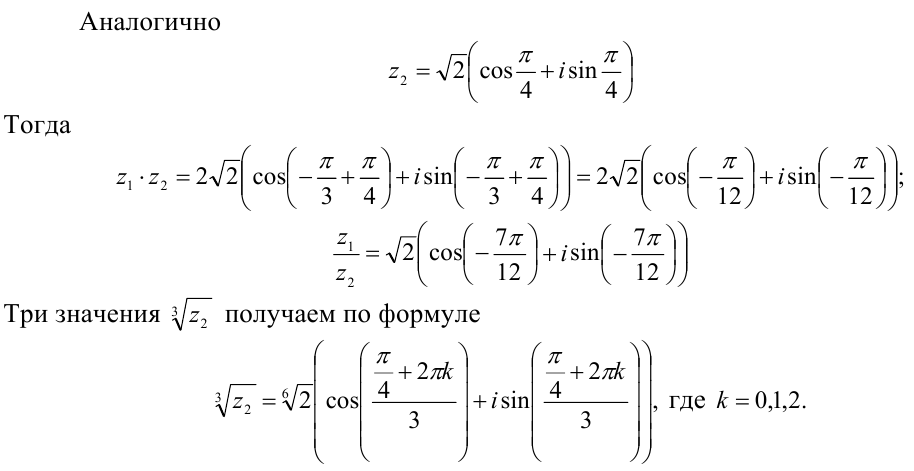
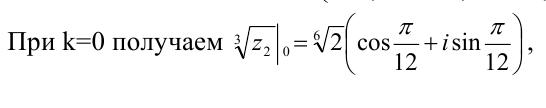
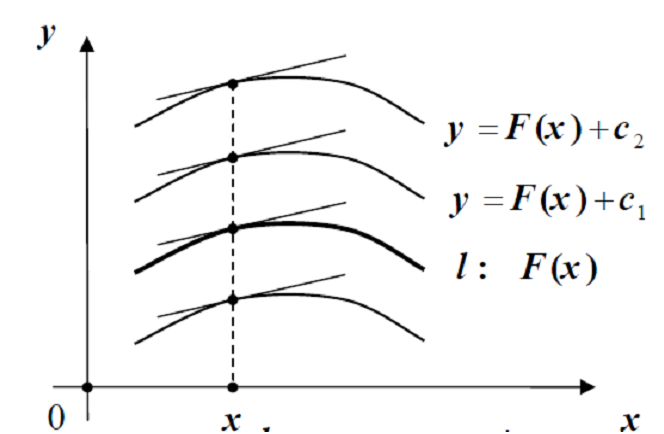
11.Первообразная. Понятие неопределенного интеграла.
12.
Свойства неопределенного интеграла.
13. Таблица основных неопределенных интегралов.
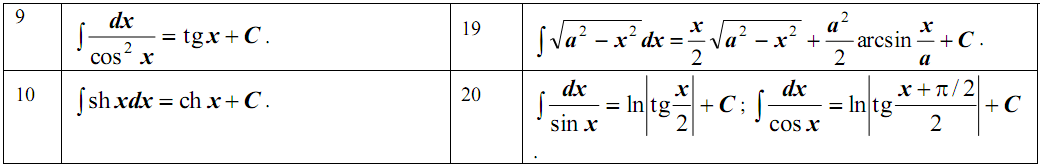
14. Непосредственное интегрирование, подведение под знак дифференциала.