Особенности применения теста Чоу

1. Если число параметров во всех уравнениях кусочно-линейной модели и единой модели одинаково и равно k, то формула (5) упрощается:

2. Тест Чоу позволяет сделать вывод о наличии или отсутствии структурной стабильности в изучаемом временном ряде. Если F_факт < F_табл, то это означает, что уравнения первого и второго кусков описывают одну и ту же тенденцию, а различия численных оценок их параметров а₁ и а₂, а также b₁ и b₂ соответственно статистически незначимы. Если же F_факт > F_табл, то гипотеза о структурной стабильности отклоняется, что означает статистическую значимость различий оценок параметров уравнений первого и второго кусков линейной зависимости.

3. Применение теста Чоу предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях кусков и независимость их распределений.

Если гипотеза о структурной стабильности тенденции ряда у_t отклоняется, дальнейший анализ может заключаться в исследовании вопроса о причинах этих структурных различий и более детальном изучении характера изменения тенденции. Эти причины обусловливают различия оценок параметров уравнений кусков.

Возможны следующие сочетания изменения численных оценок параметров этих уравнений:

– изменение численной оценки свободного члена уравнения тренда а₂ по сравнению с а₁ при условии, что различия между b₁ и b₂ статистически незначимы. Геометрически это означает, что прямые (1) и (2) параллельны. В данной ситуации можно говорить о скачкообразном изменении уровней ряда у_t в момент времени t* при неизменном среднем абсолютном приросте за период;

– изменение численной оценки параметра b₂ по сравнению с b₁ при условии, что различия между а₁ и а₂ статистически незначимы. геометрически это означает, что прямые (1) и (2) пересекают ось ординат в одной точке. В этом случае изменение тенденции связано с изменением среднего абсолютного прироста временного ряда, начиная с момента времени t*; при неизменном начальном уровне ряда в момент времени t = 0;

– изменение численных оценок параметров а₁ и а₂, а также b₁ и b₂. Геометрически это означает, что изменение характера тенденции сопровождается изменением как начального уровня ряда, так и среднего уровня за период абсолютного прироста.

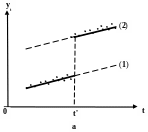
Рис.2. Изменение тенденции временного ряда при различном сочетании статистической значимости изменений параметров а₁ и а₂; b₁ и b₂:

а – статистически значимым является различие только между а₁ и а₂;

б – статистически значимым является только различие между b₁ и b₂;

в – статистически значимым является различие между а₁ и а₂; а также между b₁ и b₂:

3. Один из статистических методов тестирования при применении перечисленных выше ситуаций для характеристики тенденции изучаемого временного ряда был предложен американским экономистом Дамодаром Гуйарати. Этот метод основан на включении в модель регрессии фиктивной переменной Z_t, которая принимает значения 1 для всех t < t*, принадлежащие промежутку времени до изменения характера тенденции, далее – промежутку (1), и 0 значения для всех t > t*, принадлежащие промежутку времени после изменения характера тенденции, далее – промежутку (2). Гуйарати предлагает определять параметры следующего уравнения регрессии:

y_t = a + bZ_t + ct + d(Z_tt) + ε_t (7)

Таким образом, для каждого промежутка времени получим следующие уравнения:

Промежуток (1) Z = 1 y_t = (a + b) + (c + d)t + ε_t;

Промежуток (2) Z = 0 y_t = a + ct + ε_t.

Сопоставив полученные уравнения с уравнениями кусков, можно заметить, что

а₁ = (а + b); b₁ = (c + d);

a₂ = a; b₂ = c. (8)

Параметр b есть разница между свободными членами первого и второго уравнений кусков, а параметр d – разница между параметрами b₁ и b₂ уравнений кусков. Оценка статистической значимости различий а₁ и а₂, а также b₁ и b₂ эквивалентна оценке статистической значимости параметров b и d уравнения (7). Эту оценку можно провести при помощи t-критерия Стьюдента.

Таким образом, если в уравнении (7) b является статистически значимым, а d – нет, то изменение тенденции вызвано только различиями параметров а₁ и а₂ (рис. 2а). Если в этом уравнении параметр d статистически значим, а b – незначим, то изменение характера тенденции вызвано различиями параметров b₁ и b₂ (рис. 2б). Наконец, если оба коэффициента b и d являются статистически значимыми, то на изменение характера тенденции повлияли как различия между а₁ и а₂, так и различия между b₁ и b₂ (рис. 2в).

Этот метод можно использовать не только в дополнение к тесту Чоу, но и самостоятельно для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда. Основное его преимущество перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнений тренда.

Данный тест, а также модель (7) с фиктивной переменной, может использоваться при проверке гипотез о структурной стабильности и в более сложных моделях взаимосвязи двух и более временных рядов.

4. Общая процедура идентификации одномерного временного ряда на основе методологии Бокса-Дженкинса. Рассмотрим модели временных рядов в узком смысле, т.е. модели, объясняющие поведение временного ряда, исходя исключительно из его значений в предыдущие моменты времени.

Известно, что статистические свойства стационарных и нестационарных временных рядов существенно различаются, и для их моделирования должны применяться различные методы. Обратимся прежде всего к вопросам моделирования стационарных временных рядов, поскольку многие временные ряды могут быть приведены к стационарным после операции выделения тренда, сезонной компоненты или взятия разности.

Рассмотрим различные примеры нестационарных временных рядов.

Тренд

Рассмотрим следующий временной ряд:

y_t = α + t + ε_t (1)

Здесь ряд представлен в виде композиции детерминированной составляющей α + t (линейный тренд) и случайной составляющей ε_t, являющейся стационарным временным рядом с нулевым средним. Часто встречаются и другие примеры тренда: квадратичный α + t + t² ; экспоненциальный αе^t и т.п.

Для того чтобы выделить тренд в модели (1) и ей подобных, можно применить обычную технику оценивания параметров регрессионных уравнений, считая t независимой переменной. После этого мы получим ряд остатков, для описания которого можно будет применить модели стационарных временных рядов.

Сезонность

В экономических данных часто встречается сезонная компонента. Например, в квартальных данных может наблюдаться сезонная компонента с периодом 4:

y_t = S(t) + ε_t , S(t + 4) ≡ S(t) (2)

Здесь ряд y_t представлен в виде композиции периодической детерминированной составляющей S(t) (сезонная компонента) и случайной составляющей ε_t, являющейся стационарным временным рядом с нулевым средним. Сезонную компоненту S(t) можно представить в виде

S(t) = ₁d_1t + ₂d_2t + ₃d_3t + ₄d_4t,

где d_i – фиктивные (бинарные) переменные для кварталов.

Для выделения сезонной компоненты мы можем применить методы оценивания параметров регрессий к уравнению

y_t = ₁d_1t + ₂d_2t + ₃d_3t + ₄d_4t + ε_t (3)

Часто модель (3) представляют в виде регрессии с ограничениями, включая в нее константу:

y_t = α + ₁d_1t + ₂d_2t + ₃d_3t + ₄d_4t + ε_t, Σ_i = 0 (4)

В (4) коэффициенты _i представляют отклонение от среднего за год уровня в квартале i.

Как и в случае выделения тренда, методы моделирования стационарных временных рядов применяются далее к ряду остатков регрессии (3).