7. Первая теорема подобия

Кратко эту теорему можно сформулировать следующим образом:

у подобных процессов некоторые соотношения параметров, называемые критериями подобия, численно одинаковы.

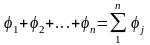- первый процесс,

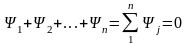– второй процесс.

, -> . ->

, -> , ->

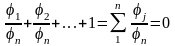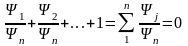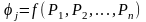, -> P₁ = n₁R₁, P₂ = n₂R₂, …, P_n = n_nR_n . ->

₁ = N₁₁ , ₂ = N₂₂,…, _n = N_n_n, -> . ->

, , …, , -> .

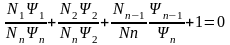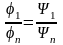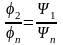8. Вторая теорема подобия

Эта теорема, известная также под названием  теоремы, гласит: всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено зависимостями между критериями подобия.

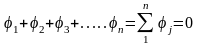
. -> f( P₁ ,P₂ ,…P_k ,…P_S ,…,P_m)=0 .

->

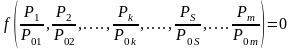
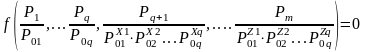P₀₁ = P₁ ; P₀₂ = P₂ ; ….; P_0q = P_q ->

. , ->

, ….. -> .

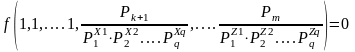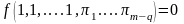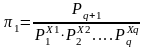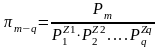9. Третья теорема подобия

Формулировка: необходимыми и достаточными условиями для создания подобия является пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия изучаемого явления.

. , ……. .

; .

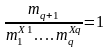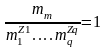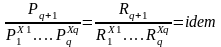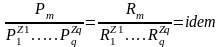Но согласно  - теореме, один из m – q критериев подобия является функцией остальных и автоматически соблюдается при их равенстве. Таким образом, очевидно, что равенства m – q – 1 критериев вполне достаточно для обеспечения возможности подобия процессов.

Величины, характеризующие однозначность процесса, обязательно входят в дифференциальное уравнение, если оно полное. Тогда можно формулировать третью теорему так: подобие любых двух систем создается при пропорциональности всех сходственных величин в этих системах и равенстве m – q – 1 критериев подобия, определенных согласно  - теореме из полного уравнения (системы уравнений) процесса.

10. Определение критериев подобия определяемых путем привидения физического процесса к безразмерному виду.

Данный способ является наиболее простым и поэтому часто применяется на практике. Он основывается на известном свойстве физических уравнений, который состоит в том, что все члены уравнения физического процесса имеют одинаковые размерности относительно основных единиц измерения.

Запишем уравнение для вертикальной оси в следующем виде

,

где D = d /dt , D_x = d / dx , D_y = d / dy , D_z = d /dz - операторы дифференцирования.

Делением на последнее слагаемое левой части придаем уравнению безразмерную форму

, , ,

, , , .

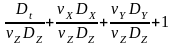
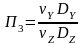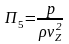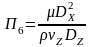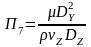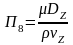С учетом равенств [D_t] = [t^-1] , [D_X] = [x^-1] , [D_Y] = [y^-1] , [D_Z] = [z^-1] и выражений

X=x / l₀ , Y = y / l₀ , Z = z / l₀ , V_X =_x /₀ , V_Y = _y / ₀ , V_Z = _z / ₀ получаем , , , ,

, , , .

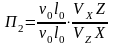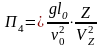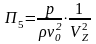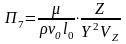Получаем: ₁ = l₀ /(₀ t); ₂ = gl₀ / ² ; ₃ = p / (²); ₄ =  .(l₀)

Используя рассмотренный метод получения критериев подобия, можно при решении ряда задач сократить число определяющих критериев за счет соответствующего выбора масштабов приведения.