3. Проблема идентификации

При переходе от приведенной формы модели к структурной возникает проблема идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.

Рассмотрим проблему идентификации для случая с двумя эндогенными переменными. Пусть структурная модель имеет вид:

где – совместные зависимые переменные.

Из второго уравнения можно выразить у₁ таким образом:

Тогда в системе имеем два уравнения для эндогенной переменной у₁ с одним и тем же набором экзогенных переменных, но с разными коэффициентами при них:

Наличие двух вариантов для расчета структурных коэффициентов одной и той же модели связано с неполной ее идентификацией. Структурная модель в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n(n – 1 + m) параметров. Так, при n = 2 и m = 3 полный вид структурной модели следующий:

Как видим, модель содержит 8 структурных коэффициентов, что соответствует выражению n(n – 1 + m).

Приведенная форма модели содержит nm параметров, для нашего примера это 6 коэффициентов (δ_ij). Действительно, приведенная форма имеет вид:

Теперь на основе 6 коэффициентов приведенной модели нужно определить 8 коэффициентов структурной модели, что, естественно, не может привести к единственности решения.

Чтобы получить единственно возможное решение для структурной модели, нужно сделать некоторые допущения относительно структурных коэффициентов, например, равенство нулю некоторых из них. Пусть, например, а₁₃ = а₂₁ = 0, тогда

В такой модели число структурных коэффициентов равно числу приведенных коэффициентов, равно 6.

Уменьшение числа структурных коэффициентов возможно и другим путем, например, путем приравнивания некоторых коэффициентов друг другу.

С позиций идентифицируемости структурные модели можно подразделить на три вида:

– идентифицируемые;

– неидентифицируемые;

– сверхидентифицируемые.

Модель идентифицируема, если все ее структурные коэффициенты определяются однозначно по коэффициентам приведенной формы модели, т.е. когда число параметров структурной модели равно числу параметров приведенной формы модели.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов. Структурная модель в полном виде (1), содержащая n эндогенных и m предопределенных переменных в каждом уравнении системы, всегда неидентифицируема.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенной формы можно получить два и более значений одного структурного коэффициента.

Так, если в структурной модели полного вида (1) положить не только а₁₃ = а₂₁ = 0, но и а₂₂ = 0, то система станет сверхидентифицируемой:

В ней пять структурных коэффициентов не могут быть однозначно определены из шести коэффициентов приведенной формы модели. Эта модель практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно уравнение системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение системы было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Пусть Н – число эндогенных переменных в j-м уравнении системы;

D – число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение.

Тогда условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Если:

D + 1 = H – уравнение идентифицируемо;

D + 1 < H – уравнение неидентифицируемо;

D + 1 > H – уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновременных уравнений:

Первое уравнение точно идентифицируемо, т.к. в нем три эндогенные переменные – у₁, у₂ и у₃, т.е. Н = 3 и две экзогенные переменные – х₁ и х₂, число отсутствующих переменных равно двум – х₃ и х₄, D = 2.

Имеем, D + 1 = H, т.е. 2 + 1 = 3, т.е. уравнение идентифицируемо.

Во втором уравнении системы Н = 2 (у₁ и у₂) и D = 1 (x₄). Имеем,

D + 1 = H, т.е. 1 + 1 = 2, следовательно, уравнение идентифицируемо.

В третьем уравнении системы Н = 3 (у₁, у₂, у₃), а D = 2 (x₁ и х₂). Следовательно, D + 1 = H – и это уравнение идентифицируемо.

Предположим, что в рассматриваемой модели а₂₁ = 0 и а₃₃ = 0.

Тогда система примет вид:

Первое уравнение этой системы не изменилось. Второе уравнение имеет Н = 2 и D = 2 (x₁, x₄). Данное уравнение сверхидентифицируемо, так как

2 + 1 > 2. Третье уравнение также сверхидентифицируемо, т.к. Н = 3

(у₁, у₂, у₃) и D = 3 (x₁, x₂, x₃), т.е. D + 1 > H или 3 + 1 > 3. Модель в целом является сверхидентифицируемой.

Предположим, что последнее уравнение с тремя эндогенными переменными данной системы имеет вид:

т.е. в него включены еще две экзогенные переменные – х₁ и х₂. В этом случае уравнение становится неидентифицируемым, т.к. при Н = 3, D = 1 (нет только х₃) и D + 1 < H, 1 + 1 < 3. Поэтому и вся модель становится неидентифицируемой и не имеет статистического решения.

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное правило отражает необходимое, но не достаточное условие идентификации.

Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой отличен от нуля, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Обратимся к следующей структурной модели:

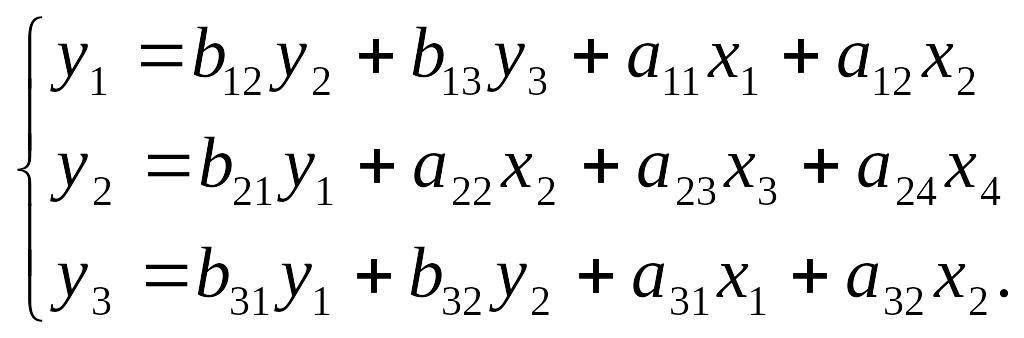
Проверим каждое уравнение системы на необходимое и достаточное условия идентификации. Для первого уравнения Н = 3 (у₁, у₂, у₃) и D = 2

(нет х₃ и х₄), т.е. D + 1 = H и необходимое условие выполнено. Для проверки на достаточное условие заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных, в которой определитель матрицы равен нулю:

Уравнения	Переменные
	x3	x4
2 3	a23 0	a24 0

Следовательно, достаточное условие идентификации не выполняется, и первое уравнение нельзя считать идентифицируемым.

Для второго уравнения Н = 2 (у₁ и у₂), D = 1 (отсутствует х₁). По счетному правилу D + 1 = H, т.е. необходимое условие идентификации выполняется. Для проверки достаточного условия составим таблицу коэффициентов при отсутствующих во втором уравнении переменных.

Уравнения	Переменные
	y3	x1
1 3	b23 -1	a11 a31

Согласно таблице, detA ≠ 0, ранг матрицы равен 2, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее числа эндогенных переменных в системе без одного. Итак, достаточное условие выполняется, второе уравнение идентифицируемо.

Третье уравнение системы имеет Н = 3 и D = 2, т.е. D + 1 = H, т.е. необходимое условие выполняется. Для проверки достаточного условия составим таблицу коэффициентов при отсутствующих в третьем уравнении переменных. в которой detA = 0:

Уравнения	Переменные
	x3	x4
1 2	0 b23	0 a24

Из таблицы видно, что достаточное условие не выполняется, поэтому уравнение неидентифицируемо.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны ± 1. В этом случае хотя само тождество и не требует проверки на идентификацию, но оно участвует в проверке на идентификацию собственно структурных уравнений системы.

Например, рассмотрим эконометрическую модель экономики страны:

где

у₁ – расходы на конечное потребление данного года;

у₂ – валовые инвестиции в текущем году;

у₃ – расходы на заработную плату в текущем году;

у₄ – валовой доход за текущий год;

х₁ – валовой доход предыдущего года;

х₂ – государственные расходы текущего года;

А – свободный член уравнения;

ε – случайные ошибки.

В этой модели четыре эндогенные переменные – у₁, у₂, у₃, у₄, причем переменная у₄ задана тождеством. Поэтому практически статистическое решение необходимо только для первых трех уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределенных переменных – экзогенную х₂ и лаговую х₁.

в рассматриваемой модели первое уравнение системы точно идентифицируемо, т.к. выполняются необходимое (Н = 3, D = 2 и D + 1 = H) и достаточное условия, т.е. ранг матрицы равен 3, а detA = – a₃₁≠ 0, что видно из следующей таблицы:

Уравнения	y2	x1	x2
2 3 4	-1 0 1	a21 a31 0	0 0 1

Второе уравнение также идентифицируемо, т.к. выполнены необходимое (Н = 2, D = 1 и D + 1 = H) и достаточное условия: ранг матрицы равен трем и detA = – b₃₄ ≠ 0:

Уравнения	y1	y4	x2
1 3 4	-1 0 1	b14 b34 -1	0 0 1

Аналогично третье уравнение системы также идентифицируемо: Н = 2, D = 1, D + 1 = H и detA = 1 ≠ 0; r = 3.

Уравнения	y1	y2	x2
1 2 4	-1 0 1	0 -1 1	0 0 1

Идентификация уравнений достаточно сложна. На структурные коэффициенты модели могут накладываться и другие ограничения, а также могут накладываться ограничения на дисперсии и ковариации остаточных величин.