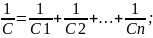- •1 . Элементарные заряды. Объемная, поверхностная и линейная плотность зарядов.
- •4 . Примение «т» Гаусса-Остроградского для расчета поля.
- •5 . Работа сил электростатического поля.
- •6 . Связь напряженности эсп с градиентом потенциала.
- •7. Электрический момент системы зарядов.
- •9 . Диэлектрическая проницаемость веществ. «т» Гаусса-Остроградского для диэлектриков.
- •1 0. Проводники в электрическом поле.
- •11. Электроемкость уединенного проводника.
- •1 2. Конденсаторы. Электроемкость системы двух проводников.
- •13. Соединения конденсаторов.
- •1 4. Энергия электростатического поля.
- •15. Сила тока и плотность тока.
- •2 0. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи.
- •21. Закон Био-Савара-Лапласа. Вектор напряженности и индукции магнитного поля.
- •2 2. Применение закона б-с-л для магнитного поля.
- •2 3. Магнитный момент контура с током.
- •2 4. Закон полного тока.
- •25. Сила Ампера и сила Лоренца.
- •26. Релятивистская природа магнитного поля.
- •2 7. Движение заряженной частицы в электрическом и магнитном поле.
- •28. Эффект Холла.
- •29. Магнитный поток. Работа по перемещению проводника с током в магнитном поле.
- •30. Явление электромагнитной индукции. Закон Фарадея.
- •31. Индуктивность контура. Явление самоиндукции.
- •32. Экстратоки. Переходные процессы.
- •33. Собственная энергия тока. Энергия магнитного поля.
- •37. Магнитная восприимчивость и проницаемость. Типы магнетиков.
- •38. Орбитальный диамагнетизм.
- •3 9. Ферромагнетизм. Домены. Кривая намагничивания ферромагнетика. Петля гистерезиса.
- •40. Первое уравнение Максвелла. Вихревое электрическое поле.
- •41. Второе уравнение Максвелла. Ток смещения.
- •42. Система уравнений Максвелла.
- •43. Плоская волна в диэлектрике.
- •44. Отражение и преломление эмв на границе двух диэлектриков.
- •45. Вектор Умова–Пойтинга.
9 . Диэлектрическая проницаемость веществ. «т» Гаусса-Остроградского для диэлектриков.
Внутреннее
поле связанного заряда: Евн=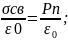 Поле
в объеме диэлектрика: E=E0+Eвн;
Или, в проекции на направление E.
E=E0-Eвн=E0
-
Поле
в объеме диэлектрика: E=E0+Eвн;
Или, в проекции на направление E.
E=E0-Eвн=E0
-
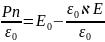 ;
=> E(1+X)=E0
=>
ε0=
;
=> E(1+X)=E0
=>
ε0=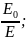 Диэлектрическая
проницаемость
ε
зависит от рода вещества и его состояния
и именно эту безразмерную величину
обычно используют для характеристики
диэлектрика. εε0
– абсолютная диэлектрическая
проницаемость. Граничные
условия: Рассмотрим границу двух
диэлектриков σ1,σ2
– плотность связанных зарядов. σ –
плотность свободных зарядов. ET1=ET2;
Нормальная составляющая испытывает
скачок: En2-En1=
Диэлектрическая
проницаемость
ε
зависит от рода вещества и его состояния
и именно эту безразмерную величину
обычно используют для характеристики
диэлектрика. εε0
– абсолютная диэлектрическая
проницаемость. Граничные
условия: Рассмотрим границу двух
диэлектриков σ1,σ2
– плотность связанных зарядов. σ –
плотность свободных зарядов. ET1=ET2;
Нормальная составляющая испытывает
скачок: En2-En1=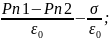 или Dn2-Dn1=σ.
или Dn2-Dn1=σ.
1 0. Проводники в электрическом поле.
П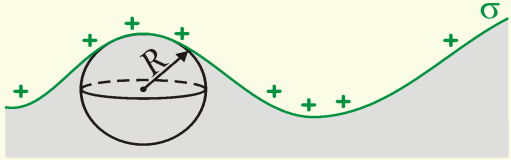 роводник
– тело (среда), в которой возникает
движение зарядов (электрический
ток),
если напряженность Е в какой-либо точке
внутри отлична от нуля.
Носители
заряда: в металлах – электроны, в газах
– ионы и электроны. Уединенным
– называют проводник, который удален
от других проводников и зарядов. Для
такого проводника можно записать: 1) в
состоянии равновесия поле во всех точках
проводника равно нулю.
внутренний
объем остается электронейтральным, но
на поверхности появляются индуцированные
заряды.
Эти
заряды компенсируют внешнее поле в
объеме проводника. Внутренний объем
проводника можно удалить, тогда такой
проводник будет экранировать поле всех
внешних зарядов.
2)
объем проводника и его поверхность
имеют одинаковый
потенциал. Потенциал
проводника
– потенциал эл. поля на его поверхности.
3) Избыточный заряд распределяется по
поверхности проводника. Толщина слоя
мала и сравнима с межатомным расстоянием.
Плотность заряда велика там, где мал
радиус кривизны поверхности (т.е. на
углах и остриях).
Действительно,
рассмотрим малый элемент поверхности:
φ=k
роводник
– тело (среда), в которой возникает
движение зарядов (электрический
ток),
если напряженность Е в какой-либо точке
внутри отлична от нуля.
Носители
заряда: в металлах – электроны, в газах
– ионы и электроны. Уединенным
– называют проводник, который удален
от других проводников и зарядов. Для
такого проводника можно записать: 1) в
состоянии равновесия поле во всех точках
проводника равно нулю.
внутренний
объем остается электронейтральным, но
на поверхности появляются индуцированные
заряды.
Эти
заряды компенсируют внешнее поле в
объеме проводника. Внутренний объем
проводника можно удалить, тогда такой
проводник будет экранировать поле всех
внешних зарядов.
2)
объем проводника и его поверхность
имеют одинаковый
потенциал. Потенциал
проводника
– потенциал эл. поля на его поверхности.
3) Избыточный заряд распределяется по
поверхности проводника. Толщина слоя
мала и сравнима с межатомным расстоянием.
Плотность заряда велика там, где мал
радиус кривизны поверхности (т.е. на
углах и остриях).
Действительно,
рассмотрим малый элемент поверхности:
φ=k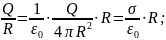 Поскольку
φ
= const на поверхности проводника,
то плотность заряда велика там, где
велика кривизна поверхности.
Поскольку
φ
= const на поверхности проводника,
то плотность заряда велика там, где
велика кривизна поверхности.
11. Электроемкость уединенного проводника.
Рассмотрим
уединенный заряженый проводник в виде
шара, пусть R-радиус;
Q-заряд,
помещенный в бесконечный однородный
диэлектрик. Потенциал заряженного шара:
φ=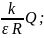 Для
проводника любой формы: φ~Q,
Введем коэффициент C
такой, что φ=
Для
проводника любой формы: φ~Q,
Введем коэффициент C
такой, что φ=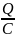 ;
[C]
= 1 Ф (Фарад)
С
– электроемкость уединенного пр-ка.
Например,
для шара: C=
;
[C]
= 1 Ф (Фарад)
С
– электроемкость уединенного пр-ка.
Например,
для шара: C=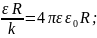 Емкость
проводника зависит
от:
1) размеров; 2) формы; 3) электрических
свойств среды; не
зависит от:
1) заряда; 2) потенциала; 3) агрегатного
состояния проводника.
Емкость
проводника зависит
от:
1) размеров; 2) формы; 3) электрических
свойств среды; не
зависит от:
1) заряда; 2) потенциала; 3) агрегатного
состояния проводника.
1 2. Конденсаторы. Электроемкость системы двух проводников.
Потенциал в т.А уменьшится, а, значит, емкость увеличится. Оказывается выгодным располагать рядом с заряженным телом другие проводники на возможно меньшем расстоянии.
Рассмотрим
сферический конденсатор. Разность
потенциалов между обкладками:
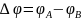 =
=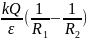 ;
Для любого конденсатора:
;
Для любого конденсатора:
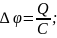 C
– электроемкость конденсатора. Для
сферического конденсатора: C=
C
– электроемкость конденсатора. Для
сферического конденсатора: C=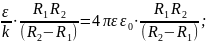 Для плоского: R1R2=R2
->
Для плоского: R1R2=R2
->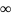 ;
R2-R1=d,
получаем С=
;
R2-R1=d,
получаем С=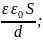
13. Соединения конденсаторов.
а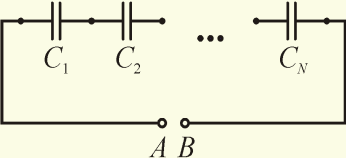
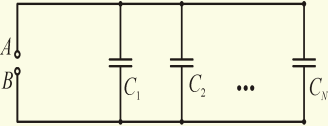 )Параллельное
соединение. Разность потенциалов UAB
для всех конденсаторов является общим
UAB=U1=U2=…=Un;
C=
)Параллельное
соединение. Разность потенциалов UAB
для всех конденсаторов является общим
UAB=U1=U2=…=Un;
C=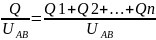 =
=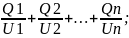 следовательно,
емкость системы конденсаторов при
параллельном соединении: C=C1+C2+…+Cn;
следовательно,
емкость системы конденсаторов при
параллельном соединении: C=C1+C2+…+Cn;
б) при последовательном соединении заряды на всех конденсаторах Q1=Q2=…=Qn=Q;
 =
=