1 . Элементарные заряды. Объемная, поверхностная и линейная плотность зарядов.

Единица измерения заряда: [Q] = 1 Кл

В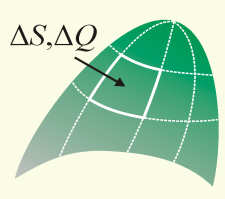 ещество состоит из трех типов стабильных частиц: электрон, протон, нейтрон. Считается, что величина заряда не зависит от скорости движения (υ < 0,5c). Заряд любого тела Q=q_eN_e+q_pN_p, где N_e-электронов, а N_p-число протонов. Если N_e=N_p – тело электрически нейтрально, N_e<N_p – тело заряжено положительно, N_e>N_p – тело заряжено отрицательно. Закон сохранения электрического заряда: алгебраическая сумма зарядов в электрически изолированной системе остается неизменной [при любых взаимодействиях, происходящих в ней].

Распределенный заряд: разобьем тело на n-частей. ∆V- малый объем, ∆Q – заряд.

Тогда ρ=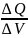 объемная плотность заряда в данной точке. ρ=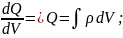 [ρ] = 1 Кл/м³

σ=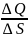 – поверхностная плотность заряда. σ=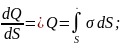 [σ] = 1 Кл/м²

Аналогично определяют и линейную плотность заряда τ=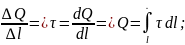

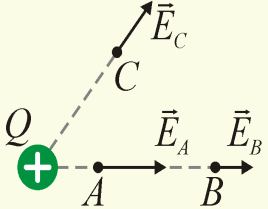
2. Поле точечного заряда. Точечным называют заряд, распределенный по телу, размерами которого можно пренебречь. Рассмотрим неподвижный т.з. Q > 0 он является источником электрического поля, которое убывает с расстоянием E=k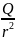 – напряженность электрического поля (ЭП), точечного заряда (т.з.), Q на расстоянии r от него. E=k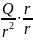 – вектор напряженности ЭП – радиус-вектор. k=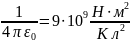 – электрическая постоянная. ε₀=8.85∙10^-12 Ф/м.

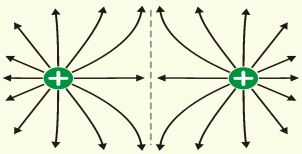
П оле положительного и отрицательного точечного заряда-----------------------

Если в точку ЭП с напряженностью поместить т.з. q, то на заряд q, со стороны ЭП, будет действовать сила. F=qE; q>0: F↑↑E; q<0: F↑↓E.

Это выражение используется для определения напряженности ЭП в точке:

э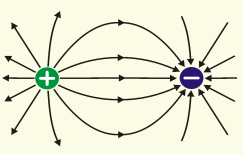 то величина, равная отношению силы, с которой поле действует на положительный заряд, помещенный в данную точку, к величине этого заряда. E=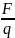 ; Закон Кулона (1785) – F₂₁=k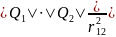 ; Сила взаимодействия двух неподвижных т.з. в вакууме пропорциональна зарядам Q₁ и Q₂ и обратно пропорциональна квадрату расстояния r₁₂ между ними. Одноименные заряды - отталкиваются, а разноименные – притягиваются. Принцип суперпозиции: Если поле создано системой точечных зарядов, то результирующее поле является суммой полей каждого из зарядов: E=E₁+E₂+…+E_N; Если двигаться в пространстве в направлении вектора, то получаются линии, начинающиеся на и заканчивающиеся на зарядах.

Один способ – рисовать поле стрелками, другой – изображать силовыми линиями. Силовые линии – линии, касательные к которым в любой точке совпадают по направлению с вектором. При таком способе изображения силового поля густота линий пропорциональна E.

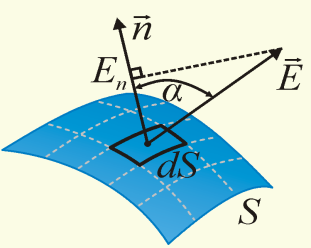
3. Теорема Гаусса-Остроградского. Поток вектора напряженности. элементарный поток:

d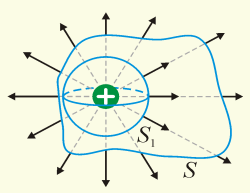 Ф=(E∙dS); dS=dSn = > dФ=EdS∙cosα=EndS.

Интегральный поток вектора равен сумме элементарных потоков: Ф=∫(E∙dS)=∫EndS;

Окружим т.з. произвольной замкнутой поверхностью S.

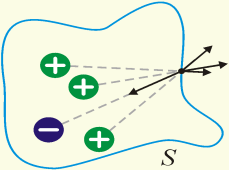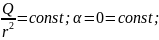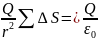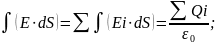П оток вектора: Ф=∑E∆S∙cosα; Для более простого случая S₁ – сферы с радиусом r получаем: E=k Тогда: Ф=k ; Этот результат будет справедливым для замкнутой поверхности любой формы, т.к. сферу и поверхность S пронизывает одинаковое число силовых линий. Если поверхность S охватывает несколько зарядов, тогда,по принципу суперпозиции, запишем: E=∑Ei => Ф= это математическая запись теоремы Гаусса-Остроградского для ЭСП; Поток вектора напряженности ЭСП через произвольную замкнутуюповерхность равен алгебраической сумме зарядов, заключенных внутрь этой поверхности, деленной на ε₀. Эта теорема является обобщением принципа суперпозиции и закона Кулона.