Средняя арифметическая простая

Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:

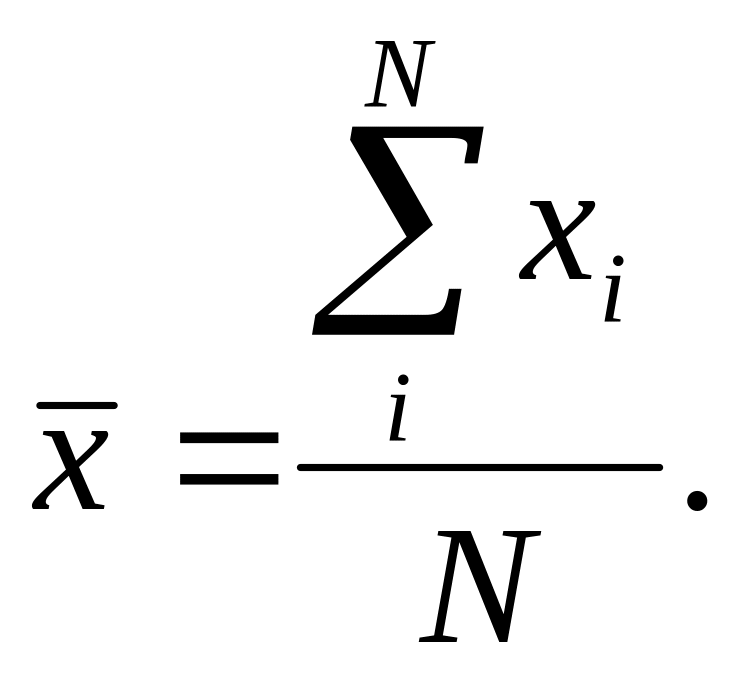
Например, известна сменная выработка рабочих бригады токарей:

табельный номер рабочего	1	2	3	4	5
количество изготовленных деталей, шт.	21	19	20	18	21

Требуется определить среднюю выработку бригады.

Для ее нахождения используется формула средней арифметической простой:

Средняя арифметическая простая рассчитывается как:

Средняя арифметическая взвешенная

Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин.

где - частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.

Пример: рассчитать среднюю продажную цену товара по данным, приведенным в таблице 5.1:

Таблица 5.1 - Объём продаж и цена товара А в магазинах города

Магазины	Продажная цена единицы товара, руб.	Объем продаж, шт.
Космос	20	25000
Ариадна	18	40000
Вега	19	40000
Итого	?	105000

Использовать среднюю арифметическую простую в данном случае нельзя, так как в разных магазинах продано разное количество товара А. Для расчёта средней продажной цены товара А. следует применить среднюю арифметическую взвешенную:

При применении средней арифметической простой средняя продажная цена товара составляла бы: х = (20 + 18 + 19) / 3 = 19 руб. , т.е. оказалась бы завышенной.

Средняя гармоническая простая

Имеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когда статистическая информация не содержит частот по отдельным значениям признака, а представлена произведением значения признака на частоту. Средняя гармоническая как вид степенной средней выглядит следующим образом:

Если исходные данные несгруппированны, то применяется средняя гармоническая простая:

К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.

Рассмотрим пример использования средней гармонической простой:

Три предприятия производят микроволновые печи. Себестоимость их производства на 1-ом предприятии составила 4000 руб., на 2-ом - 3000 руб., на 3-ем – 5000 руб. Необходимо определить среднюю себестоимость производства микроволновой печи при условии, что на каждом предприятии общие затраты на ее изготовление составляют 600 тыс. руб.

Применять среднюю арифметическую в данном случае нельзя, так как предприятия выпускают разное количество микроволновых печей: первое – 150 шт. (600000/4000); второе – 200 шт. (600000/3000); третье – 120 шт. (600000/5000).

Среднюю себестоимость микроволновой печи можно получить, если общие затраты трех предприятий разделить на общий выпуск:

К аналогичному результату можно прийти, используя формулу средней гармонической простой: