
- •Глава I. Аналитическая геометрия………………………………………….……4
- •Карточка.
- •Глава I. Аналитическая геометрия.
- •1.1 Векторы
- •1.2 Прямая и плоскость.
- •1.3 Задачи на нахождение уравнения прямой/плоскости.
- •Делаем чертеж:
- •1.4 Задачи на угол м/у прямыми, плоскостями, прямой и плоскостью.
- •1.5 Задачи на точку пересечения прямых, прямой и плоскости.
- •1.6 Задачи на проекцию.
- •1.7 Задачи на симметрию.
- •Глава II. Матрицы
- •2.1 «Тривиальные» действия
- •2.2Ранг матрицы
- •2.3 Определитель матрицы.
- •2.4 Обратная матрица.
- •2.5 Совместность. Зависимость. Базис
- •2.6 Системы уравнений.
- •2.7 Собственные векторы.
- •Глава III. Пределы.
- •Глава IV. Производные и дифференциалы.
- •4.1 «Тривиальные» производные.
- •4.2 Уравнения касательной и нормали к графику функций.
- •1) Производная в точке, заданная неявно.
- •Уравнение касательной к графику функций в точке.
- •Уравнение нормали к графику функций.
- •4.3 Производная функции нескольких переменных.
- •4.4 Градиент. Производная по направлению.
- •4.5 Первый и второй дифференциал.
- •4.6 Касательная плоскость.
- •4.7 Формулы Тейлора и Маклорена.
- •Глава V. Интегралы.
- •5.1 Свойства интегралов и таблица первообразных.
- •5.2 Метод частичной замены переменной.
- •5.3 Метод замены переменной.
- •5.4 Определенный интеграл.
- •5.5 Двойные интегралы.
- •Глава VI. Точки экстремума функции нескольких переменных.
- •6.1 Локальный экстремум функции.
- •6.2 Локальный условный экстремум.
- •6.3 Метод Лагранжа.
2.3 Определитель матрицы.
Правила:
Определитель существует только у квадратной матрицы.
Определитель не изменится, если к одной из строк матрицы прибывать другую, умноженную на число.
Если в матрице поменять 2 строки местами, то знак определителя сменится на противоположный.
Если все элементы строки матрицы умножить на число, то и определитель будет умножен на это число.
Если в матрице есть нулевая строка, то определитель равен нулю.
Способы нахождения определителя:
Матрица 2х2:
 =
a*d – b*c
=
a*d – b*c
Матрица 3х3:



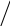

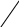
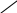
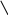
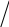

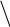

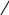
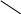

 =
+
+
-
-
-
=
+
+
-
-
-
Определитель матрицы 3х3 равняется сумме произведений элементов матрицы, обозначенных выше.
Общий метод (метод миноров и алгебраических дополнений)
Чтобы найти определитель любой матрицы нужно выбрать строку/столбец, содержащую/ий наибольшее кол-во нулей (так удобнее). И далее раскладывать определитель по элементам строки/столбца:
 +…
+…
Где
i
– номер строки, j
– номер столбца,
 - элемент матрицы стоящий в i–той
строке, j-том
столбце,
- элемент матрицы стоящий в i–той
строке, j-том
столбце,
 -
определитель матрицы, остающийся после
вычеркивания из матрицы А i–той
строки, j-того
столбца.
-
определитель матрицы, остающийся после
вычеркивания из матрицы А i–той
строки, j-того
столбца.
Повторить с каждым элементом выбранной строки/столбца.
Примеры:
3.12(д)
 =
2*3*10+0*16*0+5*1*(-1) – 5*3*0 – 2*16*(-1) – 1*0*10= 87
=
2*3*10+0*16*0+5*1*(-1) – 5*3*0 – 2*16*(-1) – 1*0*10= 87
3.19(з)
 .
Вычислим этот определитель, разложив
по элементам второго столбца (т.к. в нем
больше всего нулей):
.
Вычислим этот определитель, разложив
по элементам второго столбца (т.к. в нем
больше всего нулей):

 =
- 3*(2*4*2+3*1*3+1*3*2 – 3*4*1 – 2*2*1 – 3*3*2) +
2*(2*1*1+3*0*3+1*(-1)*4 – 3*1*1 – 2*4*0 – 1*(-1)*3)=5
=
- 3*(2*4*2+3*1*3+1*3*2 – 3*4*1 – 2*2*1 – 3*3*2) +
2*(2*1*1+3*0*3+1*(-1)*4 – 3*1*1 – 2*4*0 – 1*(-1)*3)=5
2.4 Обратная матрица.
Матрица, обратная матрице 2х2.

Общий вид.
Чтобы найти обратную матрицу необходимо отдельно найти каждый ее элемент.

Где
i
– номер строки, j
– номер столбца,
 - элемент обратной
матрицы стоящий в i–той
строке, j-том
столбце,
- элемент обратной
матрицы стоящий в i–той
строке, j-том
столбце,
 - элемент матрицы А, стоящий в j-той
строке, i-ом
столбце (т.е. наоборот),
-
определитель матрицы, остающийся после
вычеркивания из матрицы А j–той
строки, i-того
столбца. Можно заметить, что
- элемент матрицы А, стоящий в j-той
строке, i-ом
столбце (т.е. наоборот),
-
определитель матрицы, остающийся после
вычеркивания из матрицы А j–той
строки, i-того
столбца. Можно заметить, что
 - лишнее, но, записывая его, вы делаете
себе напоминание, что из матрицы мы
«вычеркиваем» j–тую
строку, i-тый
столбец, а не наоборот, для получения
матрицы В.
- лишнее, но, записывая его, вы делаете
себе напоминание, что из матрицы мы
«вычеркиваем» j–тую
строку, i-тый
столбец, а не наоборот, для получения
матрицы В.
Пример:
3.20(д)
Найти матрицу, обратную .
.
 2*2*1
– 1*(-1)*(-1)+0*0*(-1) – 0*2*(-1) – 0*(-1)*1 – 2*(-1)*(-1)=1
2*2*1
– 1*(-1)*(-1)+0*0*(-1) – 0*2*(-1) – 0*(-1)*1 – 2*(-1)*(-1)=1









Ответ:

2.5 Совместность. Зависимость. Базис
I) Теорема Кронекера – Копелли: система уравнений (матрица) называется совместной, если rang A=rang B. Где А – матрица слева от черты, а В – вся матрица полностью, т.е.:
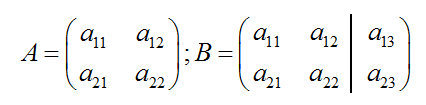
Пример:

При
каких значениях параметра а система
уравнений совместна: С= ?
?


 .
.
Матрица
А= ,
а ее ранг = 2. Матрица В=
,
а ее ранг = 2. Матрица В= ,
а ее ранг равен 2, если а+4=0, и равен трем,
если а+4
,
а ее ранг равен 2, если а+4=0, и равен трем,
если а+4 0.
Исходя из теоремы, а= 0.
0.
Исходя из теоремы, а= 0.
Система векторов называется зависимой, если определитель матрицы, составленной по этой системе, равен нулю или если после приведения к треугольному виду она имеет нулевую строку (одно из двух).
Пример:
3.13.
При каких значениях параметра
 произвольный вектор в пространстве R3
можно разложить по векторам
произвольный вектор в пространстве R3
можно разложить по векторам
 ,
,
 ,
, ?
?
Запишем
систему векторов в виде матрицы:
 .
Чтобы в этом пространстве можно было
разложить любой вектор, необходимо,
чтобы их система была независима, а
значит определитель нашей матрицы не
должен равняться 0.
.
Чтобы в этом пространстве можно было
разложить любой вектор, необходимо,
чтобы их система была независима, а
значит определитель нашей матрицы не
должен равняться 0.
 =
=
 =>
=>

Задачи на базис:
3.10.
В
линейном пространстве симметричных
матриц 2х2 найдите координаты элемента
 в базисе
в базисе
 ,
,
 ,
, .
.

= +
+ +
+ =
=
 =>
=>


2(x+y)+x+z=2 <=> 2+x – 2=2 => x=2, y= - 1, z= - 2.
Ответ: (2;-1;-2).
P.S. чтобы доказать, что эти векторы – базис, нужно записать полученную систему уравнений в виде матрицы, привести ее к треугольному виду, если она не содержит нулевых строк – это базис.
