
- •1. Основные понятия
- •2. Динамическое представление сигналов
- •5. Ряды Фурье периодических сигналов
- •7. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры гауссовского сигнала, ф-ции Дирака, Хевисайда
- •12. Свойства автокорреляционной функции.
- •1 3. Функция автокорреляции дискретных сигналов
- •6. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры постоянного напряжения, гармонического сигнала, прямоугольного и ам импульса.
- •15. Амплитудно-модулированный радиосигнал
- •16. Дискретизация узкополосных сигналов
- •17. Сигналы с угловой модуляцией. Чм и фм.
- •18. Сигналы с угловой модуляцией. Чм и фм.
- •19. Принципы построения вч модуляторов
- •14. Виды модуляции. Условие узкополосности
12. Свойства автокорреляционной функции.
Физическая реализуемость сигнала
М
![]() ногие
радиотехнические системы работают с
сигналами, одинаковыми по форме, но
сдвинутыми по фазе. Параметр
ногие
радиотехнические системы работают с
сигналами, одинаковыми по форме, но
сдвинутыми по фазе. Параметр
- временя задержки.
сигнал s(t)
можно представить в виде:
![]() ,
где
,
где
![]() .
.
М![]()
![]() ера
различия сигналов - расстояние между
ними в пространстве сигналов:
ера
различия сигналов - расстояние между
ними в пространстве сигналов:
![]() Обозначим
x1=x(t),
а x2=x(t-)=x,
тогда
Обозначим
x1=x(t),
а x2=x(t-)=x,
тогда![]() ,
,
где Exx - взаимная энергия сигналов.
если 0, то и 0. можно записать:
![]()
где![]() ----
автокорреляционная функция (АКФ) (функция
корреляции).
----
автокорреляционная функция (АКФ) (функция
корреляции).
Применим равенство Парсеваля:
![]()
![]() - энергетический
спектр сигнала.
- энергетический
спектр сигнала.
Окончательно получим:
![]()
![]()
![]()
Не каждый сигнал с известной функцией автокорреляции реализуем на практике. Должно выполняться условие:
![]() .
.
реально можно получить только те сигналы, энергетический спектр которых не принимает отрицательных значений.
Н![]() апример
сигнал с АКФ, изображённой на рисунке
сверху, практически реализовать
невозможно, т.к. его энергетический
спектр принимает значения, меньшие
нуля, а вот сигнал с АКФ, изображённой
снизу, реализуем.
апример
сигнал с АКФ, изображённой на рисунке
сверху, практически реализовать
невозможно, т.к. его энергетический
спектр принимает значения, меньшие
нуля, а вот сигнал с АКФ, изображённой
снизу, реализуем.
особенность реальных АКФ - её вторая производная в нуле всегда отрицательна:
![]() .
.
Если формировать
сигнал по известной АКФ с помощью
формирующего фильтра, то существует
критерий Винера - Пэли: реализуются лишь
те фильтры, для которых
![]() .
например
.
например
![]() реализуется,
а
реализуется,
а
![]() не реализуется. Это подтверждает тот
факт, что функция Гаусса не реализуема
на практике.
не реализуется. Это подтверждает тот
факт, что функция Гаусса не реализуема
на практике.
1 3. Функция автокорреляции дискретных сигналов
Дискретный сигнал: x={x1,x2,...,xn}.
дискретная АКФ:![]()
р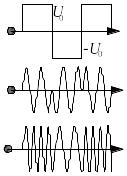 /м
сигнал, весь интервал существования
которого разделён на целое число M>1
позиций. На каждой позиции сигнал может
находиться в одном из двух состояний,
которым отвечают числа +1 и –1. Формируются
/м
сигнал, весь интервал существования
которого разделён на целое число M>1
позиций. На каждой позиции сигнал может
находиться в одном из двух состояний,
которым отвечают числа +1 и –1. Формируются
п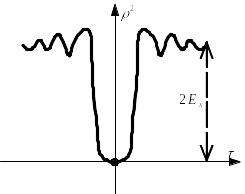 о-разному.
применяется амплитудное, фазовое или
частотное кодирование (см. рисунок).
Действующая модель такого сигнала –
последовательность чисел {Ui},
каждое из которых может принимать
значения ±1. "Пустые" позиции, на
которых сигнал не определён, обозначаются
нулями. Важнейшая операция с таким
сигналом - сдвиг сигнала на некоторое
число позиций без изменения его формы:
о-разному.
применяется амплитудное, фазовое или
частотное кодирование (см. рисунок).
Действующая модель такого сигнала –
последовательность чисел {Ui},
каждое из которых может принимать
значения ±1. "Пустые" позиции, на
которых сигнал не определён, обозначаются
нулями. Важнейшая операция с таким
сигналом - сдвиг сигнала на некоторое
число позиций без изменения его формы:
…0 0 1 –1 1 0 0 0…
…0 0 0 1 -1 1 0 0…
…0 0 0 0 1 -1 1 0…
Определим корреляционную функцию для трёхпозиционного сигнала, {1;1;1}:
…0 1 1 1 0 0 0 0…
…0 0 1 1 1 0 0 0…
…0 0 0 1 1 1 0 0…
…0 0 0 0 1 1 1 0…
п![]()
![]() ри
n=3
не происходит наложение сигналов и
преобразование становится =0, поэтому
для АКФ:
ри
n=3
не происходит наложение сигналов и
преобразование становится =0, поэтому
для АКФ:
чем уже основной лепесток АКФ, тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.
с![]()
![]()
![]()
![]()
![]() игналы
(коды) Баркера
обладают свойством: независимо от числа
позиций M
значения их АКФ при n≠0
не превышают единицы; в то же время их
энергия K(0)=M.
Сигналы Баркера реализуются лишь при
M=2,3,4,5,7,11,13.
Структурная схема для вычисления
дискретной функции автокорреляции
может иметь такой вид:
игналы
(коды) Баркера
обладают свойством: независимо от числа
позиций M
значения их АКФ при n≠0
не превышают единицы; в то же время их
энергия K(0)=M.
Сигналы Баркера реализуются лишь при
M=2,3,4,5,7,11,13.
Структурная схема для вычисления
дискретной функции автокорреляции
может иметь такой вид:
![]()
![]()
6. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры постоянного напряжения, гармонического сигнала, прямоугольного и ам импульса.
Пусть сигнал x(t) - одиночный импульс конечной длительности. мысленно представим периодическую последовательность, которая может быть представлена в виде ряда Фурье: , где .
устремим к бесконечности интервал наблюдения: T∞. И вернёмся к одиночному импульсу
Р/м базисные функции вида:
, где .
функция (s,t) описывается выражением . Тогда ,
а сигнал представим в виде .
Распишем теперь Ck как скалярное произведение:
Устремим в этом соотношении T∞., тогда d, а дискретная переменная стремится к непрерывной: k. и для x(t) получим:
, (1)
В формуле (1) внутреннее скалярное произведение - прямое преобразование Фурье,
а внешнее – обратное преобразование Фурье. Запишем их в виде системы:
- спектральная плотность сигнала x(t) или интеграл Фурье. краткая форма записи:
;
такое преобразование справедливо только для абсолютно интегрируемых сигналов.
Спектральная плотность прямоугольного импульса
![]()
Спектральная постоянного напряжения
x(t)=A0=const.
![]() .
.
S()=2πA0()
Спектральная плотность гармонического сигнала x(t)=A0cos(0t+φ).
Воспользуемся формулой Эйлера:
![]() .Тогда:
.Тогда:
![]()
![]()
Спектральная плотность АМ сигнала x(t)=A(t)cos0t..
Для A(t)
есть своя спектральная плотность
![]() .
.
![]()
![]() .
.
![]() .
.
Э![]() то
справедливо если ∆=0.
то
справедливо если ∆=0.
Энергию сигнала можно вычислить по его спектру: если A0∆ - энергия исходного сигнала, то для модулированного сигнала энергия равна . она вдвое меньше. из-за того, что у косинуса действующее значение сигнала ~ корень из 2. Чтобы энергия не терялась, нужно умножить на функцию, где действующее значение = амплитудному.
