2. Динамическое представление сигналов

Суть метода: реальный сигнал приближённо представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени:

. (1.1)

Динамическое представление - устремить к нулю длительность отдельных элементарных сигналов, и в пределе получить точное представление исходного сигнала. Есть 2 способа динамического представления.

1 представление ступенчатой функцией (функцией Хевисайда). приближённо записываем сигнал как сумму таких функций:

.

П ерейдём к пределу при Vt 0. Тогда дискретную переменную kVt можно заменить непрерывной переменной .

(1.2)

2 с помощью прямоугольных импульсов.:

(1.3)

Формулы - интегралами наложения или интегралами Дюамеля. Из них получаем соотношение: .

И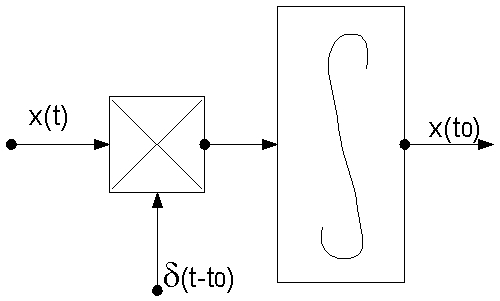 з формулы: если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен импульс. структурная схема устройства, осуществляющего измерение мгновенных значений аналогового сигнала.

О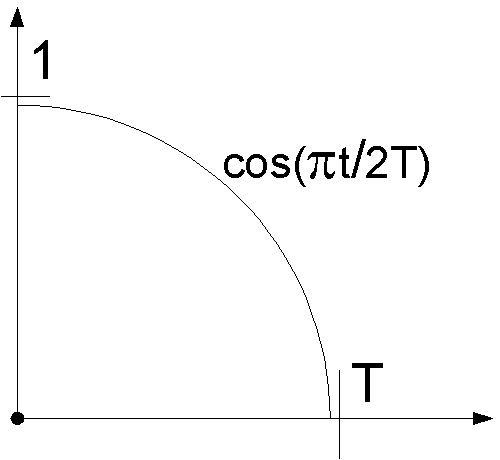 но будет состоять из перемножителя и интегратора. Измерение величины мгновенного значения будет тем точнее, чем короче реальный сигнал, который приближённо представляет дельта-функцию.

Использ-ние динамич-го представления сигналов

у стройства моделируется линейными цепями. На входной сигнал любая цепь действует неким оператором, в итоге получается выходной сигнал. Цепи, для которых этот оператор является линейным, также называются линейными цепями.

.

Для линейного оператора справедливо: .

Стационарный - оператор, для которого справедливо следующее соотношение: .

В жизни ни стационарные, ни линейные системы не существуют, но в некотором интервале наблюдения условия линейности и стационарности выполняются. Представим выходной сигнал y(t) в виде интеграла Дюамеля:

Введём переходную характеристику цепи как её реакцию на функцию Хевисайда:

.

Тогда можно записать:

(1.4)

введя импульсную характеристику системы как реакцию на функцию Дирака , можно получить:

(1.5)

В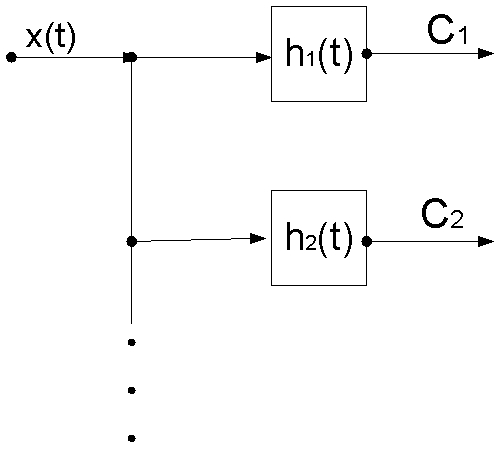 силу приведённого выше равенства ,

можно записать, что импульсная реакция цепи есть производная её передаточной характеристики, т.е. .

3. Векторное представление сигналов

Для описания сигналов в векторной форме используется бесконечномерное Гильбертово пространство. в нём вводятся следующие понятия:

1. скалярное произведение (a,b);

2. норма ||a||;

3. расстояние _ab =||a-b||

4. справедливо неравенство Шварца , (1.7)

причём = появляется в случае коллинеарности векторов a b.

Если сигнал s(t) - элемент Гильбертова пространства, то для него эти величины определяются так:

(1.8)

Введём несколько характеристик сигнала:

(1.9)

Пусть у нас есть два сигнала, которым соответствуют два вектора. Разберём свойства суммы этих векторов:

, т.е. .

сигналы, скалярное произведение которых =0 (взаимная энергия равна нулю), - ортогональные.

Примеры и ;

и .

Для ортогональных сигналов справедливо соотношение

Рассмотрим практическую задачу аппроксимации одного сигнала другим. Пусть необходимо сформировать на отрезке [0;T] кусок косинусоидального сигнала:

Такой сигнал мы сформировать не можем, но можем сформировать прямоугольный сигнал длительностью . каким должен быть параметр  для того, чтобы этот сигнал максимально аппроксимировал исходный. Для решения лучше всего подходит векторный аппарат. Представим эти сигналы в виде векторов в некотором линейном пространстве, можно утверждать, что максимальная аппроксимация будет достигнута тогда, когда норма разности этих векторов будет минимальна. Найдём это расстояние. Будем работать с его квадратом, т.к. функция квадрата монотонна и её минимуму будет соответствовать минимум расстояния:

Взяв каждый интеграл, получим:

.

Приравняв к нулю производную , получим оптимальное значение , при котором происходит наилучшая аппроксимация сигнала.

4Разложение сигналов в обобщённые ряды Фурье

разложение - представление сигнала в виде ряда:

,

где - базисные функции.

Если эти функции образуют линейно независимый координатный базис, то такое разложение единственно, т.е. если ,

то это означает, что C_k0.

Два электрических сигнала ортогональны, если (1.10)

Для разложения сигналов надо выбрать базисные функции:

или . Это тоже ортогональна. Если выполняется условие , то функции называются ортонормированными.

Тогда разложение сигнала в ряд выполняется так: .

Домножим скалярно на _i , получим:

Таким образом: (1.11)

Первая формула - обобщённыq ряд Фурье,

вторая определяет коэффициенты этого ряда.

Физический смысл этих операций - коэффициенты ряда Фурье характеризуют энергию сигнала: .

Совокупность коэффициентов {C_k} - спектр.

базис удобнее выбирать так, чтобы ряд быстрее сходился.

примеры базисных функций:

1. Экспоненциальные функции:

Этот базис является ортогональным для любого применяется для представления гармонических сигналов.

2. Система функций Уолша {wal_k()}(см. рис):

Этот базис является ортогональным на отрезке

[-0,5;0,5] и применяется для представления цифровых сигналов.

3. Система ф-ций на базе полиномов Лежандра:

, - полиномы Лежандра.

Анализатор спектра

Самая простая схема анализатора спектра. подаём сигнал на вход цепи, импульсная характеристика которой совпадает с необходимой базисной функцией. Это вытекает из того, что выражение для интеграла Дюамеля по своей структуре похоже на выражение для определения коэффициентов Фурье. В этом случае можно просто в момент времени t₁ подавать сигнал на вход цепи, а в момент t₂ снимать показания с ее выхода.