
- •1. Промежутки возрастания и убывания дифференцируемой функции. Экстремумы функции. Необходимое условие экстремума.
- •2. Достаточные условия существования максимума или минимума функции.
- •3. Наибольшие и наименьшие значения непрерывной функции на отрезке.
- •4. Исследование функции на выпуклость. Точки перегиба.
- •5. Асимптоты графика функции. Отыскание вертикальной и наклонной асимптот.
- •6. Общая схема исследования функции и построение ее графика.
- •7. Понятие о числовых рядах. Сходимость и сумма ряда. Необходимый признак сходимости.
- •8. Знакоположительные ряды. Достаточные признаки сходимости.
- •9. Свойства сходящихся рядов.
- •10. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость ряда.
- •11. Понятие о функциональных рядах. Степенные ряды. Радиус сходимости степенного ряда.
- •12. Ряды Тейлора и Маклорена.
- •1 3. Понятие о ряде Фурье. Разложение в ряд Фурье четных и нечетных периодических функций.
- •14. Первообразная функции на промежутке. Неопределенный интеграл и его свойства.
- •15. Интегрирование по частям, замена переменных. Таблица интегралов основных элементарных функций.
- •17. Основные свойства определенного интеграла. Теорема о среднем.
- •18. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница для вычисления определенного интеграла. Замена переменных в определенном интеграле.
- •19. Несобственный интеграл с неограниченной областью интегрирования. Несобственный интеграл от функции, неограниченной на отрезке интегрирования. Понятие сходимости несобственных интегралов.
- •20. Понятие о дифференциальном уравнении и его решении. Порядок дифференциального уравнения. Понятие общего и частного решения.
- •21. Задача Коши для дифференциальных уравнений первого порядка. Теорема существования и единственности решения.
- •22. Линейные дифференциальные уравнения первого порядка. Метод разделения переменных.
- •23. Комплексные числа, алгебраическая и тригонометрическая форма записи. Формула Эйлера.
- •24. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (однородные и неоднородные). Структура общего решения.
- •26. Непрерывность функции двух независимых переменных.
- •27. Частные производные и вектор градиента функции двух независимых переменных. Производная по направлению. Понятие о линиях уровня.
- •28. Полный дифференциал функции нескольких переменных. Дифференциал второго порядка функции нескольких переменных.
- •29. Частные производные и дифференциалы высших порядков.
- •30. Максимумы и минимумы функции нескольких (двух) переменных. Необходимые условия экстремума.
- •31. Наибольшее и наименьшее значения функции двух независимых переменных на замкнутом ограниченном множестве.
- •32. Достаточные условия максимума или минимума функции нескольких независимых переменных.
- •33. Предмет теории вероятностей. Виды случайных событий. Классическое определение вероятности события. Свойства вероятности.
- •34. Относительная частота события. Статистическое определение вероятности события.
- •35. Аксиоматическое определение вероятности.
- •36. Алгебра событий.
- •37. Теорема сложения вероятностей для совместных и несовместных событий.
- •38. Условная вероятность. Теорема умножения вероятностей для зависимых и независимых и событий.
- •40. Формула Бейеса (формула переоценки вероятностей гипотез).
- •41. Схема повторных независимых испытаний (схема Бернулли). Формула Бернулли.
- •42. Локальная и интегральная теоремы Лапласа.
- •43. Дискретные и непрерывные случайные величины, их законы распределения.
- •44. Числовые характеристики дискретных случайных величин.
- •46. Плотность распределения вероятностей непрерывной случайной величины, ее свойства.
- •47. Числовые характеристики непрерывных случайных величин.
5. Асимптоты графика функции. Отыскание вертикальной и наклонной асимптот.
Асимптоты функции. Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
В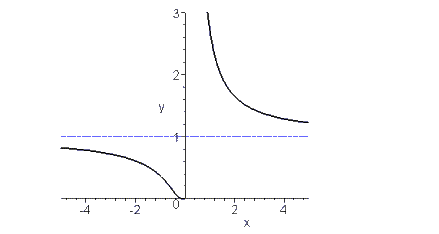 ертикальные
асимптоты.
Вертикальные асимптоты определяются
точками разрыва функции и границами
области определения. График функции,
непрерывной на всей числовой прямой,
вертикальных асимптот не имеет. Некоторые
особенности поведения функции в
окрестности вертикальных асимптот
представлено на рисунке. Вертикальные
асимптоты определяются точками разрыва
второго рода. В этом случае f (x0 ± 0) = ±
∞, или f (x0 ± 0) = + ∞ , или f (x0 ± 0) = − ∞.
Следует отметить, что в этом случае
может отмечаться всё разнообразие
поведения функции в окрестности точки
разрыва. Например, на рис. приведён
график элементарной функции.
ертикальные
асимптоты.
Вертикальные асимптоты определяются
точками разрыва функции и границами
области определения. График функции,
непрерывной на всей числовой прямой,
вертикальных асимптот не имеет. Некоторые
особенности поведения функции в
окрестности вертикальных асимптот
представлено на рисунке. Вертикальные
асимптоты определяются точками разрыва
второго рода. В этом случае f (x0 ± 0) = ±
∞, или f (x0 ± 0) = + ∞ , или f (x0 ± 0) = − ∞.
Следует отметить, что в этом случае
может отмечаться всё разнообразие
поведения функции в окрестности точки
разрыва. Например, на рис. приведён
график элементарной функции.
Наклонные асимптоты.
У![]()
![]() равнение
наклонной асимптоты функции y = f (x)
определим уравнением y =k·x + b. При этом
параметры наклонной асимптоты
определяются соотношениями
равнение
наклонной асимптоты функции y = f (x)
определим уравнением y =k·x + b. При этом
параметры наклонной асимптоты
определяются соотношениями
6. Общая схема исследования функции и построение ее графика.
Находим область определения функции f(x)
Находим точки пересечения кривой y = f(x) с осями координат и наносим их на чертеж.
Определяем, симметрична ли кривая y = f(x) относительно осей координат и начала координат.
Исследуем функцию y = f(x) на непрерывность. Если функция имеет в точке x0 разрыв, то отмечаем ее на чертеже.
Находим асимптоты кривой, если они имеются.
Находим максимум и минимум функции и отмечаем на чертеже точки кривой с максимальной и минимальной ординатами.
Исследуем кривую y = f(x) на выпуклость вверх или вниз, находим точки перегиба кривой и отмечаем их на чертеже.
Вычерчиваем кривую y = f(x).
.
7. Понятие о числовых рядах. Сходимость и сумма ряда. Необходимый признак сходимости.
Ч![]() исловой
ряд
– это сумма членов числовой
последовательности вида
исловой
ряд
– это сумма членов числовой
последовательности вида
аk называют общим членом числового ряда или k–ым членом ряда.
Сумма числового ряда a1+a2+…+an+… определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда an представляют собой либо вещественные, либо комплексные числа.
8. Знакоположительные ряды. Достаточные признаки сходимости.
Рассмотрим 2 знакоположительных ряда U1+ U2+….+ Un +…(А); V1+ V2+…+ Vn+…(В), где Un≥0, Vn≥0 ( n=1,2….)
Теорема: необходимым и достаточным условием сходимости знакоположительного ряда явл-ся ограниченность последовательности его частичных сумм.
Док-во: пусть знакоположительный ряд А- сходится и его суммой явл-ся число S. Тогда S явл-ся пределом последовательности его частичных сумм S1, S2, .., Sn,…, но как известно из сходимости числовой последовательности следует его ограниченность, т.е. сущ-ет некоторое число М такое, что Sn≤М при n=1,2.. следует ограниченность, достаточность, пусть последовательность частичных сум сходящегося ряда А- ограничена некоторым числом n, т.е. для любого n. Т.к. ряд А явл-ся знакоположительным, то последовательность его частичных сум монотонно возрастающая S1≤S2≤… Sn≤ Однако При любом n, Sn≤ n следует расмотренная последовательность частичных сум ограниченна. Это говорит о том, что эта последовательность ссходится к некоторому числу S, т.е. сходится ряд А 1-ый признак сравнения: если знакоположительные ряды А и В таковы, что Un≤ Vn (n=1,2..), то из сходимости ряда В след.сходимость ряда А, а из расходимости ряда А след.расходимость ряда В.
Док-во: пусть сходится ряд В это означает, что последовательность частичных сум этого ряда ограниченно, т.е. Sn≤М при (n=1,2..) Т.к. Un≤ Vn (n=1,2..), то S’n≤ Sn (n=1,2..), где S’n –энная частичная сумма ряда А из последовательности неравенства след.что при S’n≤М ( n=1,2..) Последнее неравенство говорит о том, что последовательность частичных сум ряда А ограниченно числом n. Отсюда след. в силу т.3.1. след сходимость ряда А. Если же ряд А расходится, то последовательность частичных сум Sn→∞( так как ряд знакоположительный). Из неравенства S’n≤ Sn след. что Sn также →∞ т.е. ряд В – расходится.
2-ой признак сравнения: если сущ-ет предел lim (n→∞) Un\ Vn=к, 0≤к≤∞, то из сходимости ряда В при к меньшим бесконечности след.сходимость ряда А, а из расходимости Ряда А при к>0 след.расходимость ряда В, таким оьразом при конечном положительном пределе к оба ряда сходятся или расходятся одновременно.
Признак Коши: если для ряда А сущ-ет с= lim (n→∞)n√ Un ( конечный или бесконечный), то при с<1, ряд А- сходится, с>1 расходится.
Признак Даламбера: если для ряда А сущ-ет предел конечный или бесконечный с= lim (n→∞) Un+1\ Un, то при с<1 ряд А сходится, с>1 расходится.
Достаточное условие
Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: S(n+1)-S(n)=a(n+1). Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится (по определению).
