29. Частные производные и дифференциалы высших порядков.
Дифференциалы
высших порядков.
Пусть
в области
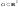задана некоторая функция
,
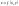имеющая непрерывные частные производные
первого порядка. Тогда она будет
дифференцируема в этой области, и ее
дифференциал имеет вид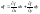
,где
- произвольные приращения независимых
переменных
.
Видим,
что
также является функцией от
.
Если существуют непрерывные частные
производные второго порядка функции
для
,
то можно говорить о дифференциале от
первого дифференциала
,
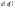который называется дифференциалом
второго порядка от
и обозначается символом
.
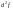Частные
производные высших порядков.
Пусть частные производные
функции z
= f
(x,
y
), определенной в окрестности точки М,
существуют в каждой точке этой
окрестности. В этом случае частные
производные представляют собой функции
двух переменных х и у, определенные в
указанной окрестности точки М. Назовем
их частными производными первого
порядка. В свою очередь, частные
производные по переменным х и у от
функций
в точке М, если они существуют, называются
частными производными второго порядка
от функции f
(М) в этой точке и обозначаются следующими
символами
Частные
производные второго порядка вида
,
,
называются смешенными частными
производными.
30. Максимумы и минимумы функции нескольких (двух) переменных. Необходимые условия экстремума.
Условия
экстремума.
Определение.Пусть функция f(x)
определена в некоторой окрестности
,
δ>0, некоторой точки
своей области определения. Точка
называется точкой локального максимума,
если в некоторой такой окрестности E
выполняется неравенство
(
),
и точкой локального минимума, если
.
Понятия локальный максимум и локальный
минимум объединяются термином локальный
экстремум. Следующая теорема даёт
необходимое условие того, чтобы точка
была точкой локального экстремума
функции f(x).
Теорема. Если точка
-
это точка локального экстремума функции
f(x),
и существует производная в этой точке
,
то
.
Доказательство этой теоремы сразу же
следует из теоремы Ферма.
Утверждение
теоремы можно переформулировать так:
если функция f(x)
имеет локальный экстремум в точке
,
то либо: 1)
,
либо 2) производная
не существует. Точка
называется
критической точкой функции f(x),
если f(x)
непрерывна в этой точке и либо
,
либо
не существует. В первом случае точка
называется также стационарной точкой
функции f(x).
Итак, локальный экстремум функции f(x)
может наблюдаться лишь в одной из
критических точек этой функции.
31. Наибольшее и наименьшее значения функции двух независимых переменных на замкнутом ограниченном множестве.
Теорема. Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области D функция z(x,y) достигает своего наибольшего M и наименьшего m значений. Можно предложить следующий план нахождения M и m:
1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы.
2. Находим стационарные точки внутри D.
3. Находим стационарные точки на каждой из границ.
4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения.