1 Основы теории графов

Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты называются вершина­ми и отмечаются точками, а связи между вершинами называются дугами и отмечаются стрелками между соответствующими точками (рисунок 1.1).

Рисунок 1.1

Такие системы и образуют графы. Граф может изображать сеть улиц в городе: вершины гра­фа – перекрестки, а дуги – ули­цы с разрешенным направлени­ем движения (улицы могут быть с односторонним и двусторонним движением). В виде графов можно представить блок – схемы про­грамм (вершины – блоки, а дуги – разрешенные переходы от одного блока к другому), электри­ческие цепи, географические карты и молекулы химических со­единений, связи между людьми и группами людей. Перейдем к точным определениям.

Графом называется алгебраическая система G= (М,R), гдеR– двухместный предикатный символ. Элементы носителя М называются вершинами графаG, а элементы бинарного отноше­нияRМ²– дугами. Таким образом, дугами являются пары вершин (a,b)R. При этом дуга (a,b) называется исходящей из вершины а и заходящей в вершинуb.

Изображение графа G= (М,R) получается путем расположения различных точек на плоскости для каждой вершиныaМ, причем если (а, b)  R, то проводится стрелка (дуга) из вершины а к вершинеb.

Пример: Изображение графа Gс множеством вершин М

{1,2,3,4} и множеством дуг R= {(1,1), (1,2), (2,3),(3, 4), (4,3), (4,1)} представлено на рисунке 1.1.

При задании графа для нас не имеет значе­ния природа связи между вершинами а и b, важ­но только то, что связь существует и информация о связях содержится во множестве дугR. Однако часто возникают ситуации, при которых такой информации оказывается недостаточно, например, в случаях, когда имеется несколько дуг, исходящих из вершины а и заходящих в вершинуb, такие дуги называются кратными (рисунок 1.2). Тогда используется понятие мультиграфа.

Рисунок 1.2.

Мулътиграфом Gназывается тройка (М,U,P), в которой М – множество вершин,U– множество дуг, а РМUМ – трехместный предикат, называемый инцидентором и представляемый следующим образом: (a,u,b)Pтогда и только тогда, когда дуга и исходит из вершины а и заходит в вершинуb. Отметим, что любой граф можно представить в виде мультиграфа.

Граф G= (M,R) называется ориентированным (орграфом), если найдется дуга (а,b)Rтакая, что (b, а)R. Если же отношениеRсимметрично, т. е. из (а,b)Rследует (b, а)R, то графGназывается неориентированным (неорграфом). Если одновременно пары (а,b) и (b, а) принадлежатR(рисунок 1.3, а), то информацию об этих дугах можно представить множеством [а,b] = {(а,b), (b, а)}, называемым ребром, которое соединяет вершины а иb. При этом вершины а иbназываются концами ребра [а,b]. Ребра изображаются линиями (без стрелок), соединяющими вершины (рисунок 1.3, б).

Рисунок 1.3.

Если в мультиграфе вместо дуг рассматриваются ребра, то мультиграф также называется неориентированным. Отметим, что если в орграфе G = (М,R) к каждой дуге (а,b)Rдобавить пару (b, а), то в результате образуется неорграф, который будем называть соответствующим данному орграфуGи обозначать черезF(G).

Пример: Орграфу G, изображенному на рисунке 1.1, соответствует неорграфF(G), изображенный на рисунке 1.4.

Рисунок. 1.4.

Информация о структуре графа может быть задана матрицей бинарного отношения. Пусть G= (М,R) – граф, в котором множество вершин имеетnэлементов: М = {a₁,a₁, …,a_n}. Матрицей смежности А_G = (A_ij) графаGназывается матрица порядкаn, определенная следующим образом:

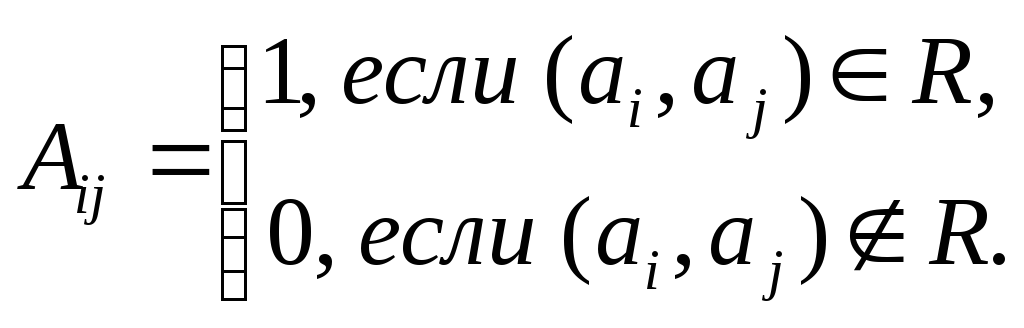
Если А_ij= 1, то вершина а_jназывается последователем вершины а_i, а а_i– предшественником а_j. Вершины а_iи а_jназываются смежными, еслиA_ij= 1 илиA_ji= 1.

Если G– мультиграф, то в матрице смежностиA_Gэлемент А_ijпо определению равен числу дуг, исходящих из вершины а_iи заходящих в вершину а_j(i,j{1, ...,n}).

Рисунок 1.5.

Граф G, изображенный на рисунке 1.1.5, имеет матрицу смежности

Отметим, что если G– неорграф, то матрица смежностиA_Gсимметрична, т. е. не меняется при транспонировании:.

Петлей в графе Gназывается дуга, соединяющая вершину саму с собой. ЕслиG– граф без петель, то в матрице смежностиA_Gпо главной диагонали стоят нулевые элементы:

Теорема 1. Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одно­временными перестановками строк и столбцов (т.е. одновременно с перестановкой i- й иj- й строк переставляютсяi- й иj- е столбцы).

Согласно этой теореме по матрице смежности граф восста­навливается однозначно с точностью до изоморфизма.

В графе G= (М,U, Р) дугаuUназывается инци­дентной вершине аМ, если (а,u,b)Р или (b,u, а)Р для некоторогоbМ. Если М = {a₁, ...,a_m},U= {u₁, ...,u_n}, то матрицей инцидентностиB_G= (В_ij) мультиграфаGна­зывается матрица размераm*n, определяемая по следующему правилу:

Рисунок. 1.6.

Пример: Мультиграф G, изображенный на рисунке 1.6, имеет матрицу инцидентности

Мультиграфы G= (M,U,P) иG' = (M',U',P') называ­ются изоморфными, если существуют биекции: ММ' и:UU' такие, что (a,u,b)Р тогда и только тогда, когда ((a),(u),(b))P’.

Аналогично теореме 1 справедлива

Теорема 2. Мультиграфы GиG' изоморфны тогда и только тогда, когда их матрицы инцидентности получаются друг из друга некоторыми перестановками строк и столбцов.

Пути и маршруты

Путем (или ориентированным маршрутом) ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является началь­ной вершиной следующей.

Так, на рис. 1.6 последовательности дуг

а₆ а₅ а₉ a₈ а₄ (1.1)

а₁ а₆ а₅ а₉ (1.2)

а₁ а₆ а₅ а₉ а₁₀ а₆ а₄ (1 3)

являются путями.

Рисунок 1.6

Дуги а = (х_i , x_j), x_i ≠ x_j , имеющие общие концевые вершины, называются смежными. Две вершины x_i и x_j называются смежными, если какая-нибудь из двух дуг (x_i, x_j) и (х_j), x_i) или обе одно­временно присутствуют в графе. Так, например, на рис. 1.6 дуги а₁, а₁₀, а₃ и а₆, как и вершины х₅ и х₃, являются смежными, в то время как дуги а₁ и а₅ или вершины х₅ и x₃ не являются смежными.

Ориентированной цепью (или, короче, орцепъю) называется такой путь, в котором каждая дуга используется не больше одного раза. Так, например, приведенные выше пути (1.1) и (1.2) являют­ся орцепями, а путь (1.3) не является таким, поскольку дуга а_в в нем используется дважды.

Простой орцепъю называется такой путь, в котором каждая вершина используется не более одного раза. Например, путь (1.2) является простой орцепью, а пути (1.1) и (1.3) — нет. Очевидно, что простая орцепь является также орцепью, но обратное утвер­ждение неверно. Например, путь (1.1) является орцепью, но не простой орцепью, путь (1.2) является орцепью и простой орцепью, а путь (1.3) не является ни орцепью, ни простой орцепью. Маршрут есть неориентированный «двойник» пути, и это понятие рассматривается в тех случаях, когда можно пренебречь направ- ленностью дуг в графе. Таким образом, маршрут есть последова­тельность ребер а₁, а₂,...,a_q , в которой каждое ребро a_i, за исключением, возможно, первого и последнего ребер, связано с ребрами а_i-1 и a_i+1 своими двумя концевыми вершинами. После­довательности дуг

а₂, a₄, a₈, a₁₀, (1.4)

a₂, a₇, а₈, а₄, а₃ (1.5)

a₁₀, a₇, а₄, а₈, а₇, а₂ (1.6)

в графе, изображенном на рис. 1.2, являются маршрутами; черта над символом дуги означает, что ее ориентацией пренебрегают, т. е. дуга рассматривается как неориентированное ребро.

Точно так же, как мы определили орцепи и простые орцепи, можно определить цепи и простые цепи. Так, например, маршрут (1.4) есть цепь и простая цепь, маршрут (1.5) — цепь, но не простая цепь, а маршрут (1.6) не является ни цепью, ни простой цепью.

Путь или маршрут можно изображать также последователь­ностью вершин, что мы и будем использовать. Путь (1.1) можно представить также последовательностью вершин х₂, х₅, x_k, х₃, х₅, х₆ и такое представление часто оказывается более полезным в тех случаях, когда осуществляется поиск простых орцепей пли простых цепей.

Веса и длина пути

Иногда дугам графа G сопоставляются (приписываются) чис­ла — дуге (x_t, xj) ставится в соответствие некоторое число с,_;-, называемое весом, или длиной, или стоимостью (ценой) дуги. Тогда граф G называется графом со взвешенными дугами. Иногда веса (числа у,) приписываются вершинам x_t графа, и тогда полу­чается граф со взвешенными вершинами. Если в графе веса при­писаны и дугам, и вершинам, то он называется просто взвешен­ным.

При рассмотрении пути μ, представленного последовательно­стью дуг (а_х, а₂, . . ., a_q), за его вес (или длину, или стоимость) принимается число I(μ), равное сумме весов всех дуг, входящих в μ, т. е.

Таким образом, когда слова «длина», «стоимость», «цена» и «вес» применяются к дугам, то они эквивалентны по содержанию, и в каждом конкретном случае выбирается такое слово, которое

Рисунок 1.3

ближе подходит по смыслу и совпадает с принятым в литературе. Длиной (или мощностью) пути и. называется число дуг, входя­щих в него.

Петли, ориентированные циклы и циклы

Петлей называется дуга, начальная и конечная вершины кото­рой совпадают. На рис. 1.7, например, дуги а₂и а₅являются пет­лями.

Путь а₁, а₂, ... ,a_qназывается замкнутым, если в немначальная вершина дуги а₁ совпадает с конечной вершиной дуги а_q. Так, например, в графе, приведенном на рис. 1.7, последова­тельности дуг

а₃ ,а₆, а₁₁, (1.7)

а₁₁ , а₃, а₄, а₇, а_i, а₁₂, а₉, (1.8)

а₃, а₄, а₇, а₁₀, а₉, а₁₁, (1.9)

являются замкнутыми путями.

Пути (1.7) и (1.9) являются замкнутыми простыми орцепями (контурами, или простыми орциклами), поскольку в них одна и та же вершина используется только один раз (за исключением начальной и конечной вершин, которые совпадают), а путь (1.8) не является контуром, так как вершинах₁ используется в нем дважды. Контур, проходящий через все вершины графа, имеетособое значение и называется гамилътоновым контуром. Конеч­но, не все графы обладают гамильтоновыми контурами. Так, например, контур (1.9) является гамильтоновым контуром графа, приведенного на рис. 1.7, а граф на рис. 1.6 не имеет гамильтоно-вых контуров, поскольку не существует такой дуги, для которойх₁ была бы конечной вершиной.

Замкнутый маршрут является неориентированным двойником замкнутого пути. Таким образом, замкнутый маршрут является маршрутом х₁, х₂, ... ,x_q, в котором совпадают начальная и конечная вершины, т. е. в которомх_х =x_q.

На рис. 1.7 маршруты

a₁, а₁₂, а₁₀, (1.10)

а₁₀, а₁, а₃, а₄, а₇, а₁, а₁₂ (1.11)

являются замкнутыми маршрутами.