Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Уфимский государственный авиационный технический университет

Кафедра вычислительной математики и кибернетики

Кафедра проектирования средств информатики

ТЕОРИЯ ГРАФОВ

Практикум

по дисциплине «Дискретная математика»

Уфа  2005

Составители: н.И. Житникова, г.И. Федорова, а.К. Галимов

УДК 519.6 (07)

ББК 22.193 (я7)

Теория графов: Практикум по дисциплине «Дискретная математика». /Уфимск. гос. авиац. техн. ун-т; Сост. Н.И. Житникова, Г.И. Федорова, А.К. Галимов. - Уфа, 2005. - 39 с.

Практикум содержит основные сведения о теории графов, примеры решения контрольных задач и задания для самостоятельной работы. Предназначен для студентов факультета информатики и робототехники специальности 010503: «Математическое обеспечение и администрирование информационных систем» и направления 230100: «Информатика и вычислительная техника», изучающих дисциплину «Дискретная математика».

Ил. 15. Библиогр.: 8 назв.

Рецензенты: Бронштейн Е.М.

Хабибуллин Б.Н.

© Уфимский государственный

авиационный технический университет, 2005

Содержание

Введение 4

1. Краткий перечень основных понятий теории графов 5

1.1. Общие понятия 5

1.2. Понятия смежности, инцидентности, степени 7

1.3. Маршруты и пути 7

1.4. Матрицы смежности и инцидентности 8

1.5. Связность. Компоненты связности 9

1.6. Матрицы достижимости и связности 9

1.7. Расстояния в графе 10

1.8. Образ и прообраз вершины и множества вершин 10

1.9. Нагруженные графы 11

1.10. Деревья и циклы 12

2. Решение контрольных задач 13

2.1. Компоненты сильной связности ориентированного графа 13

2.2. Расстояния в ориентированном графе 16

2.3. Минимальный путь в нагруженном ориентированном графе 20

2.4. Эйлеровы циклы и цепи 23

2.5. Минимальное остовное дерево 25

2. 6. Задача о коммивояжёре 27

3. Задания для самостоятельного решения 35

Список литературы 38

Введение

Теория графов – это математический аппарат для формализации (моделирования) реальных задач по исследованию свойств конечных множеств с заданными отношениями между их элементами. В их числе задачи из области администрирования сетей, информационных потоков, планирования, проектирования и управления различными системами.

Задачи на графах удобно переводить на языки программирования, то есть решать с использованием современной вычислительной техники.

Умение решать задачи на графах позволит будущему специалисту приобрести опыт разработки технологий и методов теории операций для решения задач при научных исследованиях и проектно-конструкторской деятельности

В данном практикуме рассмотрены основные типы задач на графах, подходы и методы их решения, конкретные примеры.

Цель раздела «Теория графов» состоит в формировании у студентов умений и навыков, необходимых при исследовании различных систем и проектировании технических объектов.

Для достижения указанной цели решаются следующие задачи:

- формирование знаний методов и алгоритмов эффективного решения задач дискретной оптимизации;

- формирование умений и навыков использования изученных методов для решения типовых задач математического моделирования и оценки пределов применимости полученных результатов.

1. Краткий перечень основных понятий теории графов

1.1. Общие понятия

Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 1, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.

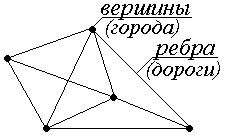
Рис. 1.

Формальное определение графа таково [1-8]. Графом Г=(V,X) называется пара множеств: V – множество, элементы которого называются вершинами, X – множество неупорядоченных пар вершин, называемых ребрами. Если v, w  V, x=(v,w)X, то говорят, что ребро x соединяет вершины v и w или x инцидентно v и w. Таким образом, {v,w} – обозначение ребра. Если Х представляет собой упорядоченные пары (т. Е. X – подмножество декартова произведения V×V), то граф называется ориентированным, а пары {v,w} называют дугами. Если множеству X принадлежат пары v=w, то такие ребра (v,v) называют петлями. Существование одинаковых пар {v,w} соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер называют количество таких одинаковых пар.

Например, кратность ребра {v₁, v₂} в графе, изображенном на рис. 2, равна двум, кратность ребра {v₃, v₄} − трем.

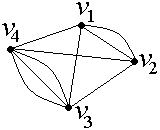
Рис.2.

Псевдограф − граф, в котором есть петли и/или кратные ребра.

Мультиграф − псевдограф без петель.

Заметим, что графом также называют мультиграф, в котором ни одна пара не встречается более одного раза.

Итак, используемые далее обозначения:

V – множество вершин;

X – множество ребер или дуг;

v (или v_i)– вершина или номер вершины;

G, G₀ – неориентированный граф;

D, D₀ – ориентированный;

{v,w} − ребра неориентированного графа;

{v,v} – обозначение петли;

(v,w) − дуги в ориентированном графе;

v,w – вершины, x,y,z – дуги и ребра;

n(G), n(D) количество вершин графа;

m(G) – количество ребер, m(D) – количество дуг.

Примеры

1) Ориентированный граф D=(V, X), V={v₁, v₂, v₃, v₄},

X={x₁=(v₁,v₂), x₂=(v₁,v₂), x₃=(v₂,v₂), x₄=(v₂,v₃)}.

Рис. 3.

2) Неориентированный граф, изображенный на рис. 4:

G=(V, X), V={v₁, v₂, v₃, v₄, v₅},

X={x₁={v₁,v₂}, x₂={v₂,v₃}, x₃={v₂,v₄}, x₄={v₃,v₄}}.

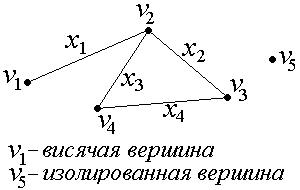
Рис. 4.