
- •38. Вероятность. Аксиоматика теории вероятностей
- •39. Комбинаторный анализ
- •40. Алгебра событий. Основные теоремы теории вероятностей
- •41.Формула полной вероятности, формула Байеса
- •42. Схема независимых испытаний. Формула Бернулли
- •43. Предельные теоремы Лапласа и Пуассона.
- •44 Случайные величины. Дискретная случайная величина
- •45. Непрерывная случайная величина
- •46.Основные распределения случайных величин
45. Непрерывная случайная величина
Функцией распределения вероятностей
называют функцию
![]() ,
определяющую вероятность того, что
случайная величина
в
результате испытания примет значение,
меньшее
,
определяющую вероятность того, что
случайная величина
в
результате испытания примет значение,
меньшее
![]() ,
то есть:
,
то есть:
![]() .
Случайную
величину называют непрерывной, если ее
функция распределения вероятностей
есть непрерывная, кусочно-дифференцируемая
функция с непрерывной производной.
.
Случайную
величину называют непрерывной, если ее
функция распределения вероятностей
есть непрерывная, кусочно-дифференцируемая
функция с непрерывной производной.
Свойства функции распределения вероятностей случайной величины
З
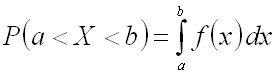
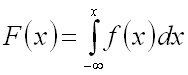 начения
функции распределения вероятностей
принадлежат отрезку
начения
функции распределения вероятностей
принадлежат отрезку
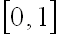 :
:
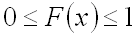 .
2.
Функция распределения вероятностей –
неубывающая функция, то есть:
.
2.
Функция распределения вероятностей –
неубывающая функция, то есть:
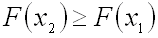 ,
если
,
если
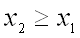 .
Следствие
1. Вероятность того, что случайная
величина примет значение, заключенное
в интервале
.
Следствие
1. Вероятность того, что случайная
величина примет значение, заключенное
в интервале
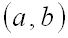 ,
равна приращению функции распределения
вероятностей на этом интервале:
.
,
равна приращению функции распределения
вероятностей на этом интервале:
.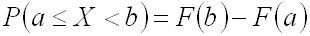 Следствие
2. Вероятность того, что непрерывная
случайная величина примет одно
определенное значение, равна
нулю.
Используя последнее следствие,
легко убедиться в справедливости
следующих равенств:
Следствие
2. Вероятность того, что непрерывная
случайная величина примет одно
определенное значение, равна
нулю.
Используя последнее следствие,
легко убедиться в справедливости
следующих равенств:
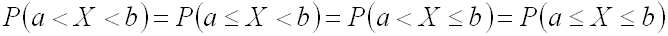 .
3.
Если возможные значения непрерывной
случайной величины принадлежат интервалу
,
то:
.
3.
Если возможные значения непрерывной
случайной величины принадлежат интервалу
,
то:
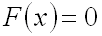 ,
если
,
если
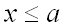 ;
;
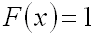 ,
если
,
если
 .
Следствие.
Если возможные значения непрерывной
случайной величины расположены на всей
числовой оси, то справедливы следующие
предельные соотношения:
.
Следствие.
Если возможные значения непрерывной
случайной величины расположены на всей
числовой оси, то справедливы следующие
предельные соотношения:
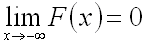
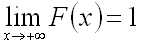 Плотностью
распределения вероятностей непрерывной
случайной величины Х называют функцию
f(x)– первую
производную от функции распределения
вероятностейF(x):f(x)=F’(x).
Таким образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей.
Теорема. Вероятность
того, что непрерывная случайная величина
Х примет значение, принадлежащее
интервалу (a,b),
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Следовательно, зная плотность
распределения вероятности f(x),
можно найти функцию распределения F(x)
по формуле
Плотностью
распределения вероятностей непрерывной
случайной величины Х называют функцию
f(x)– первую
производную от функции распределения
вероятностейF(x):f(x)=F’(x).
Таким образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей.
Теорема. Вероятность
того, что непрерывная случайная величина
Х примет значение, принадлежащее
интервалу (a,b),
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Следовательно, зная плотность
распределения вероятности f(x),
можно найти функцию распределения F(x)
по формуле
46.Основные распределения случайных величин
