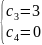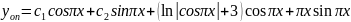Задача 1.Найти неопределённый интеграл

Решение:
=
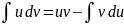
Получаем:
= (4-3x)
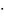
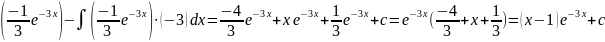
Задача 2. Вычислить определённый интеграл:

Решение:

Получаем: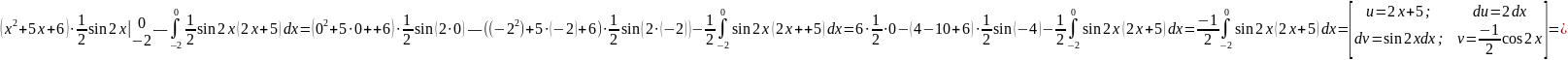
=
Задача 3. Вычислить неопределённый интеграл:

Решение:
Введем
замену: ,
тогда
,
тогда

Задача 4. Вычислить определенный интеграл:
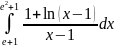
Решение:
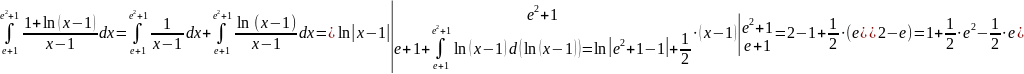
Задача 5.Вычислить неопределенный интеграл:
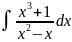
Решение:
Выделяем целую часть:
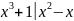
 -
- x+1
x+1
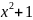
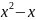
x+1
Получаем:
=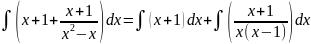
Разложим правильную рациональную дробь на дроби методом неопределенных коэффициентов:
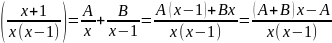

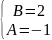
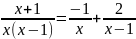
Получаем:
=
Задача 6. Вычислить неопределенный интеграл:

Решение:
Разложим
правильную рациональную дробь на дроби
методом неопределенных коэффициентов


Вычитаем из третьего уравнения четвертое:
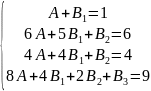
Прибавим к третьему уравнению первое умноженное на -4:

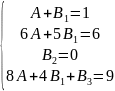
Прибавим ко второму уравнению первое умноженное на -5:

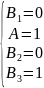
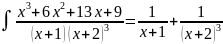
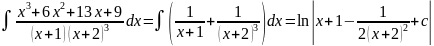
Задача 7.
Найти неопределенный интеграл:

Решение:
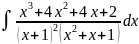
Разложим правильную рациональную дробь на элементарные дроби методом неопределенных коэффициентов:


=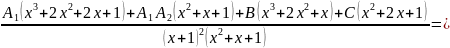
=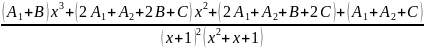
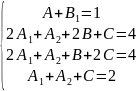
Вычтем из второго уравнения четвертое:
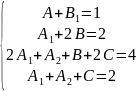
Вычтем из второго уравнения первое:
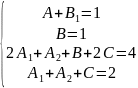


Вычитаем из третьего уравнения четвертое:
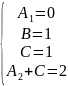


Тогда:
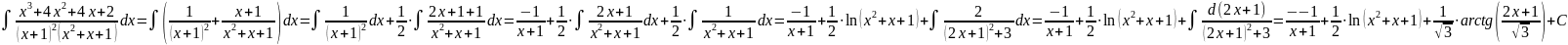
Задача 8. Вычислить определенный интеграл:
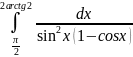
Решение:
Воспользуемся универсальный подставкой:
t=tg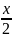
Где:
sinx= , cosx=
, cosx= , dx=
, dx=
x=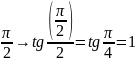
x=2arctg2
Подставляем:

Задача 9. Вычислить определенный интеграл:

Решение:
Воспользуемся подстановкой:
t=tgx
Где:
sin2x=
, dx=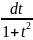
x=
x=arctg3
Подставляем:
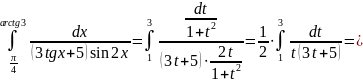
Разложим правильную рациональную дробь на элементарные дроби методом неопределенных коэффициентов:



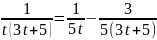
Тогда:
=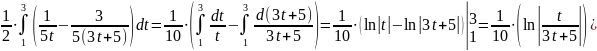
Задача 10. Вычислить определенный интеграл:
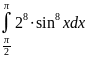
Решение:
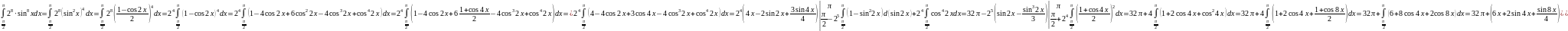
Задача 11. Вычислить определенный интеграл:

Решение:
=

dx=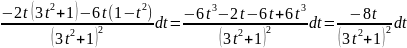
3x+1=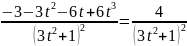
1)=
Задача 12.
Вычислить определенный интеграл:
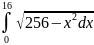
Решение:
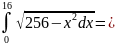 Замена:
Замена:
x=16sin
t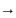 dx=16cost
dt
dx=16cost
dt
x=0
x=16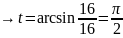
Получаем:
=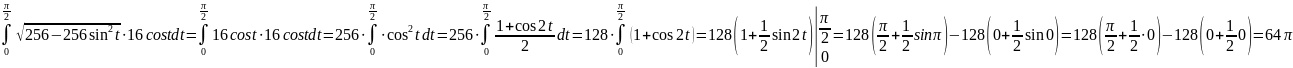
Задача 13.
Найти неопределенный интеграл:
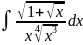
Решение:

Под
интегралом дифференциальный бином
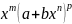 ,откуда m=-
,откуда m=-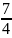 ,
n=
,
n= ,
p=
,
p=
Т.к.
 целое,
то используем замену:
целое,
то используем замену:
a ,
где s-
знаменатель дроби P.
,
где s-
знаменатель дроби P.
Т.е. в нашем случае замена имеет вид:

X=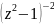
dx=-2 =-4z
=-4z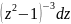
Получаем:
=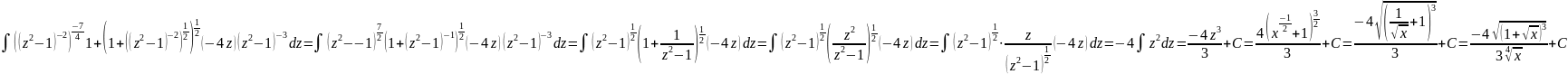
!Задача 14
Вычислить площадь фигуры, ограниченной графиками функций:
y=
На графике видно что площадь между графику состоит из двух одинаковых частей:
 =2
=2
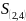
Найдем
площадь части где x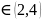 как разность двух интегралов:
как разность двух интегралов:
S=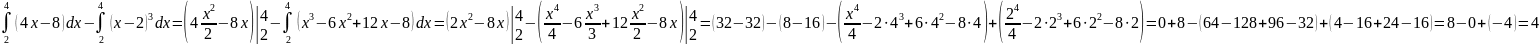
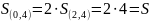
Задача 15.
Задача 16.
Задача 17.
Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат.
lnx,
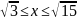
Решение:
Длина
дуги кривой, заданной уравнением y=f(x);
a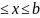 ,
определяется формулой L=
,
определяется формулой L=
Найдем производную данной функции:

 =
=
Тогда по формуле получаем:
L=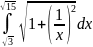 =
=
 =
=
=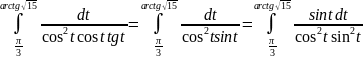 =
=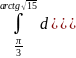 =
=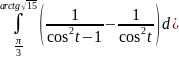
Задача 18.
Вычислить длины дуг кривых, заданных параметрическими уравнениями.
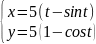

Решение:
Найдем производные по t:
 ;
;

L=5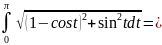 5
5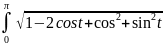 dt=
5
dt=
5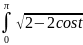 dt=5
dt=5 =10
=10
Часть 2. Дифференциальные уравнения.
Задача 1. Найти общий интеграл дифференциального уравнения.
4x

Решение:
4x
 =3
=3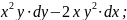
2x(2+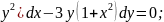
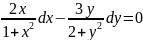
ln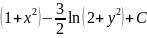
Задача 2. Найти общий интеграл дифференциального уравнения.

Решение:
Данное уравнение является однородным, поэтому делаем замену
y=ux,
u= ,
,
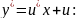
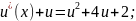

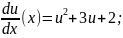
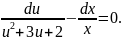
Интегрируем последнее уравнение:



Учитывая
y=
,
получим:ln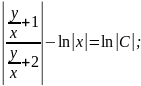 ln
ln ln
ln
Задача 3. Найти общий интеграл дифференциального уравнения.

Решение:
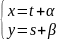
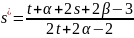
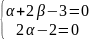
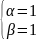

s=zt
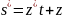
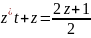

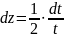
z=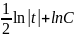
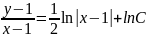
Задача 4. Найти решение задачи Коши.
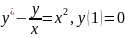
Решение:
y=uv;

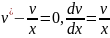 ;
;
 ln v=ln x; v=x.
ln v=ln x; v=x.
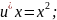
 u=
u=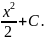
y=x
(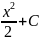 ).
).
y(1)=0
y=x
Задача 5. Решить задачу Коши.
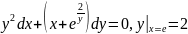
Решение: Полагаем x функций от y, x=x(y).
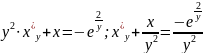 .
.
x=u
v;
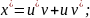
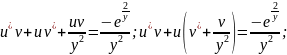

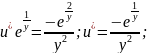 u=
u=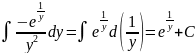
x=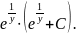
Учитывая y(e)=2, получаем:
y=

x=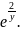
Задача 7. Найти общий интеграл дифференциального уравнения.
3
Решение:
Обозначим
М=(x,y)=3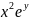 ,
N(x,y)=
,
N(x,y)=

 =
=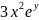
Поскольку
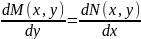 то данное уравнение представляет собой
уравнение в полных дифференциалах, то
есть существует функция U(x,y)
такая, что dU=3
dx+(
то данное уравнение представляет собой
уравнение в полных дифференциалах, то
есть существует функция U(x,y)
такая, что dU=3
dx+(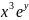 -1)dy.
По определению дифференциала имеем:
-1)dy.
По определению дифференциала имеем:
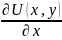 =3
,
откуда получаем
=3
,
откуда получаем
U=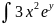 dx+
dx+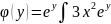 dx+
dx+ =
+
,
где
-некоторая
функция, зависящая от y.
=
+
,
где
-некоторая
функция, зависящая от y.
Дифференцируя найденную функцию U по переменной y получим:
=
+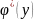 (1)
(1)
С другой стороны, из исходного уравнения следует, что
= -1 (2)
Приравнивая (1) и (2) получаем дифференциальное уравнение нахождения функция :
+ = -1
=-1
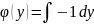 =-y+E,
где Е - произвольная постоянная.
=-y+E,
где Е - произвольная постоянная.
Таким образом получаем U(x,y)= -y+E. Но поскольку дифференциал функции U равен нулю (т.е dU=0), то U является постоянной, то есть
-y+E = D, где D-постоянная. Полученное равенство можно переписать в виде -y=, где С=D-E-произвольная постоянная.
Задача 11.
Найдите решение задачи Коши:
4 ,
,
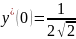
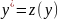

4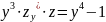

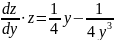
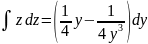


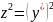
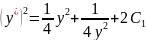
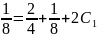
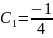
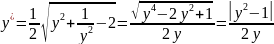
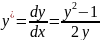

ln
x=0,
y= ln
ln
ln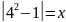
Задача 12.
Найти общее решение дифференциального уравнения:


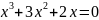
x=0 x=-1 x=-2

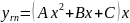
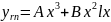
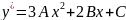
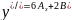


6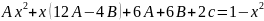

Общее решение:


Задача 13.
Найти общее решение дифференциального уравнения:
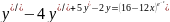
Решение:
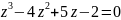
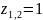


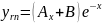

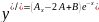
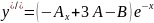
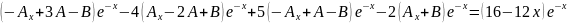
12
-12A=-12 A=1
16A-12B=16 B=0
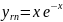

Задача 14.
Найти общее решение дифференциального уравнения:
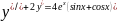
Решение:
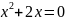
x=0 x=-2
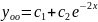

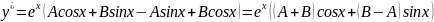
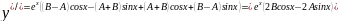
2Bcosx-2Asinx+2(A+B)cosx+2(B-A) sinx=4sinx+4cosx
(A+2B)cosx+(-2A+B)sinx=2sinx+2cosx
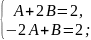


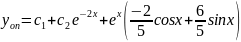
Задача 15.
Найти общее решение дифференциального уравнения:

Решение:
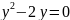
y=0 y=2

Представим
2ch2x=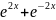


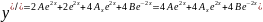

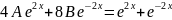
2A=1 A=
8B=1
B=
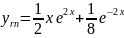

Задача 16.
Найти решение задачи Коши:
 ,
y(0)=3 ,
,
y(0)=3 ,
 =0
=0
Решение:

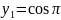
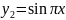
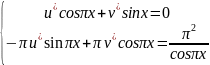
После решения системы получаем:
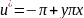

u=-π
v=π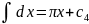

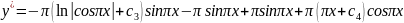
y(0)=3
3=(0+