
- •4. Метод наименьших квадратов (мнк):
- •5 . Классическая линейная модель множественной регрессии
- •Оценка точности и адекватности регресионной модели
- •Понятие мультиколлинеарности. Основные признаки и последствия мультиколлинеарности
- •Понятие мультиколлинеарности. Основные признаки мультиколлинеарности и способы ее устранения
- •1 0. Стандартизованная и естественная формы уравнения множественной регрессии. Интерпретация параметров.
- •Обобщённая линейная модель множественной регрессии в случае гетероскедастичности остатков. Взвешенный метод наименьших квадратов
- •Тесты на гетероскедастичность: их преимущества и недостатки. Тест Голдфельда-Квандта
- •13. Тесты на гетероскедастичность: их преимущества и недостатки. Тест Уайта
- •1 4. Тесты на гетероскедастичность: их преимущества и недостатки. Тест Глейзера
- •Обобщённая линейная модель множественной регрессии. Понятие автокорреляции. Тесты на наличие автокореляции: их преимущества и недостатки.
- •Обобщённая линейная модель множественной регрессии. Теорема Айткена. Обобщённый метод наименьших квадратов.
- •Понятие автокорреляции. Тесты на наличие автокорреляции. Тест Бреуша-Годфри.
- •18. Понятие автокорреляции. Тесты на наличие автокорреляции. Тест Дарбина-Уотсона.
- •Понятие гетероскедастичности остатков. Оценка параметров модели в случае гетероскедастичности.
- •23. Неоднородность данных в регрессионном смысле. Использование фиктивных переменных в регрессионных моделях. Интерпритация коэф при фиктивных переменных.
- •24. Неоднородность данных в регрессионном сиысле. Тест Чоу на неоднородность данных.
- •25. Использование фиктивных переменных в регрессионных моделях. Интерпритация коэф при фиктивных переменных.
- •27. Нелинейные модели регрессии и их линеаризация. Примеры нелинейных моделей регрессии.
- •28. Линейная и степенная модели множественной регрессии: интерпритация параметров.
- •29. Производственная Кобба-Дугласа. Эластичность объема производства.
- •45. Модель спроса-предложения и её модификации
45. Модель спроса-предложения и её модификации
Рассмотрим ряд модификаций модели спроса-предложения.
1. Модель спроса-предложения с учетом тренда.
Если предположить изменение спроса со временем, то в первое уравнение системы необходимо добавить временной тренд:

Приведенная форма модели запишется в виде:

Исходная система не оказывается идентифицируемой, поскольку параметр β5 является сверхидентифицируемым. Чтобы это показать, запишем систему в следующем виде:

Сравнивая две записи приведенной формы, легко заметить, что оценку β5. можно получить двумя способами: как e/b и f/c.
2. Модель спроса-предложения с учетом налога.
Предположим, что продавцы товаров облагаются специальным налогом T. Величина налога меняется со временем и представлена временным рядом. Тогда система уравнений запишется следующим образом:
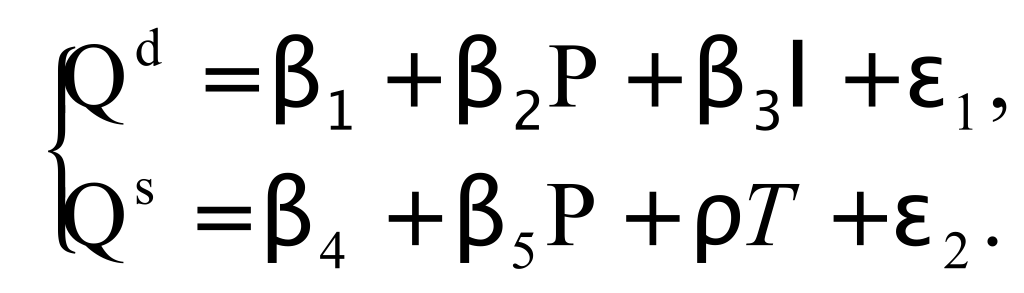
В данном случае система является идентифицируемой, но если теперь предположить, что доход I на протяжении длительного времени является постоянной величиной, то в уравнении спроса переменную I следует исключить.

Данная система уравнений уже не является идентифицируемой. Получить идентифицируемое уравнение формирования предложения можно, наложив ограничение на структурные коэффициенты: β5 = -ρ. Смысл этого ограничения в том, что мы полагаем, что продавцы исходят из суммы, которую они получают после уплаты налога, т.е. Р* = Р - Т.

Пример 6. Структурная форма модели имеет вид:
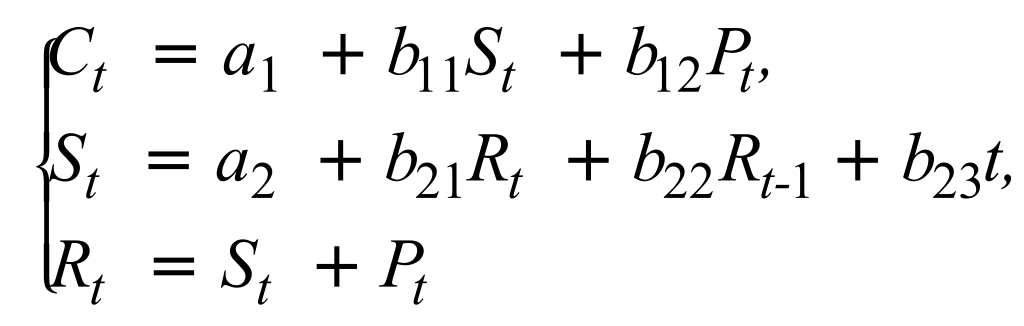
где: Сt – личное потребление в период t,
St – зарплата в период t,
Pt – прибыль в период t,
Rt – общий доход в период t,
Rt-1 – общий доход в период t-1,
Задание:
Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
Запишите приведенную форму модели.
Решение.
Модель представляет собой систему одновременных уравнений, состоящую из двух уравнений, которые необходимо проверить на идентифицируемость для определения способа оценки параметров, и тождества, параметры которого известны, поэтому необходимости в проверке его на идентифицируемость нет.
Модель включает три эндогенные переменные (Ct, St, Rt) и три экзогенные переменные (Pt, t, в том числе одну лаговую переменную Rt-1).
Проверим уравнения модели на идентифицируемость.
1 уравнение.
Проверим выполнение необходимого условия идентифицируемости. Это уравнение включает две эндогенные переменные (Ct ,St) и одну экзогенную переменную (Pt). Таким образом, H = 2; число экзогенных переменных системы, не входящих в это уравнение, также равно двум D = 2. Получаем: D + 1 > H, следовательно, первое уравнение сверхидентифицируемо.
Теперь проверим достаточное условие идентифицируемости.
Запишем матрицу коэффициентов при переменных (эндогенных и экзогенных), не входящих в первое уравнение (Rt, Rt-1, t):
Номер уравнения |
Rt |
Rt-1 |
t |
2 |
b21 |
b22 |
b23 |
3 |
-1 |
0 |
0 |
Ее ранг равен 2, так как определитель квадратной подматрицы 2х2 этой матрицы не равен нулю:
![]() ,
,
и достаточное условие идентифицируемости выполняется.
2 уравнение.
Это уравнение включает две эндогенные переменные (St ,Rt) и две экзогенные переменные (Rt-1, t). Таким образом, H = 2; число экзогенных переменных, не входящих в это уравнение, равно одному D = 1. Получаем: D + 1 = H, и второе уравнение является точно идентифицируемым.
Теперь проверим достаточное условие идентифицируемости.
Запишем матрицу коэффициентов при переменных, не входящих во второе уравнение (Ct, Pt):
Номер уравнения |
Сt |
Pt |
1 |
-1 |
b12 |
3 |
0 |
1 |
Определитель этой матрицы не равен нулю, а ее ранг равен 2:
 .
.
Таким образом, второе уравнение системы точно идентифицируемо. Но так как первое уравнение системы сверхидентифицируемо, то вся модель является сверхидентифицируемой.
Запишем приведенную форму модели в общем виде:

Здесь ν1, ν2, и ν3 - случайные ошибки.
Поскольку модель является сверхидентифицируемой, то для оценки
параметров уравнений следует применять двухшаговый метод наименьших квадратов. ♦
