9.Масштаб изображения и искажения длин линий в проекции Гаусса-Крюгера.

Проекция Гаусса-Крюгера является равноугольной, так как в ней не искажаются горизонтальные углы геометрических фигур земной поверхности. Поэтому бесконечно малые фигуры в этих проекциях подобны соответствующим фигурам на эллипсоиде. В проекции Г-К, кроте того, не искажаются длины дуг осевых меридианов. Длины других линий и площадей фигур в этой проекции получаются искаженными.

Значение искажения зависит от масштаба изображения линий в проекции, т.е. отношение длины бесконечно малого отрезка в проекции к длине соответствующего отрезка на сфероиде (шара).

Если длина малого отрезка на сфероиде (шаре) равно S, а длина его изображения в проекции к длине соответствующего отрезка на сфероиде (шаре).

Если длина малого отрезка на сфероиде (шаре) равна S, а длина его изображения в проекции Г-К-S_г, то масштаб изображения m длины линии в этой проекции можно выразить приближенным равенством

m=S_Г/S,

которое будет тем точнее, чем меньше значение S.

Относительное искажение длин линий определяется отношением

(S_г –S)/S =∆S/S= m-1

Масштаб изображения в пределах одной и той же зоны различен и зависит от удаленности отрезка от осевого меридиана.

10. Редуцирование линий на плоскости в проекции Гаусса Крюгера.

Редуцированием линии называют (вычисление) длины линии на шаре (местности) к длине линии на плоскости в проекции.

Масштаб изображения в проекции Гаусса Крюгера равен:

Sᵣ/S=m=1+y²/2R²

Из этого равенства следует, что

S²=S(1+y²/2R²) или Sᵣ=S+ΔS,

Где ΔS=Sy²/2R²=S(m-1)

Величину ΔS называют поправкой за редуцирование линии при переходе с эллипсоида (шара) на плоскость в проекции Гаусса-Крюгера. Как следует из формулы ΔS=Sy²/2R²=S(m-1), эта поправка всегда положительна, т.е. длина линий в проекции Гаусса-Крюгера всегда больше длины соответствующих линий на земной поверхности. При вычислении поправки SΔ ординату берут для середины редуцируемого отрезка (достаточно знть приближённо значение этой ординаты). Поправки за редуцирование линий в проекции Гаусса-Крюгера вводят в измеренные линии в том случае, когда в создаваемых геодезических сетях (полигонометрия, триангуляция) в качестве исходных данных используют пункты государственной геодезической сети. Эти поправки можно не вводить в измеренные линии, если их значение пренебрегаемо мало по сравнению с точностью линейных измерений.

11. Искажение площадей в проекции Гаусса-Крюгера.

В проекции Гаусса-Крюгера сохраняется подобие бесконечно малых фигур. Известно, что площади подобных фигур относятся как квадраты сходственных сторон, т. е.

Pᵣ/P=Sᵣ²/S².

Но ранее было получено

Sᵣ=S(1+y²/2R²)

Подставив это выражение для Sᵣ в предыдущее равенство, будем иметь

Pᵣ/P=(1+y²/2R²) или Pᵣ=P(1+y²/R²+ / ).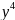

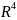Имея ввиду, что последний член в скобках мал по сравнению с предыдущим, его можно отбросить. Тогда

Pᵣ=P(1+y²/R²) или

Pᵣ=P+ΔP,

Где ΔP – поправка в площадь за переход с поверхности шара на плоскость в проекции Гаусса-Крюгера; ΔP=Py²/R²=2P(m-1).

Обычно специалистов интересует площадь не в проекции Гаусса-Крюгера, а на местности, поэтому величину ΔP называют абсолютным искажением площади.

Относительное искажение площади будет выражаться формулой

ΔP/P=y²/R/

Если площадь землепользования (колхоза, совхоза) определена по координатам на плоскости в проекции Гаусса-Крюгера Pᵣ, то для получения фактической площади землепользования на местности P необходимо вычесть поправку ΔP, т.е.

P=Pᵣ-ΔP.

Для упрощения вывода формул земная поверхность была принята за поверхность шара. Если принять Землю за эллипсоид вращения (сфероид), что ближе к действительному ее виду, то вывод формул, относящихся к проекции Гаусса-Крюгера, будет значительно сложнее. Полученные формулы, приближённые, но они обеспечивают необходимую точность при построении (разрезной) геодезической сети сгущения и съемочной сети.