
- •Расчёт конической косозубой передачи
- •Определение коэффициента режима работы
- •Определение диаметра колеса
- •Расчет диаметра вала в опасном сечении
- •Расчет вала на сопротивление усталости (выносливость)
- •Выполнить кинематическое исследование заданного механизма методом построения плана скоростей и ускорений
- •Структурный анализ механизма
- •Построение плана скоростей
- •Построение плана ускорений
Выполнить кинематическое исследование заданного механизма методом построения плана скоростей и ускорений
Частота вращения входного звена n = 150 мин -1. Масштаб механизма 1:4.
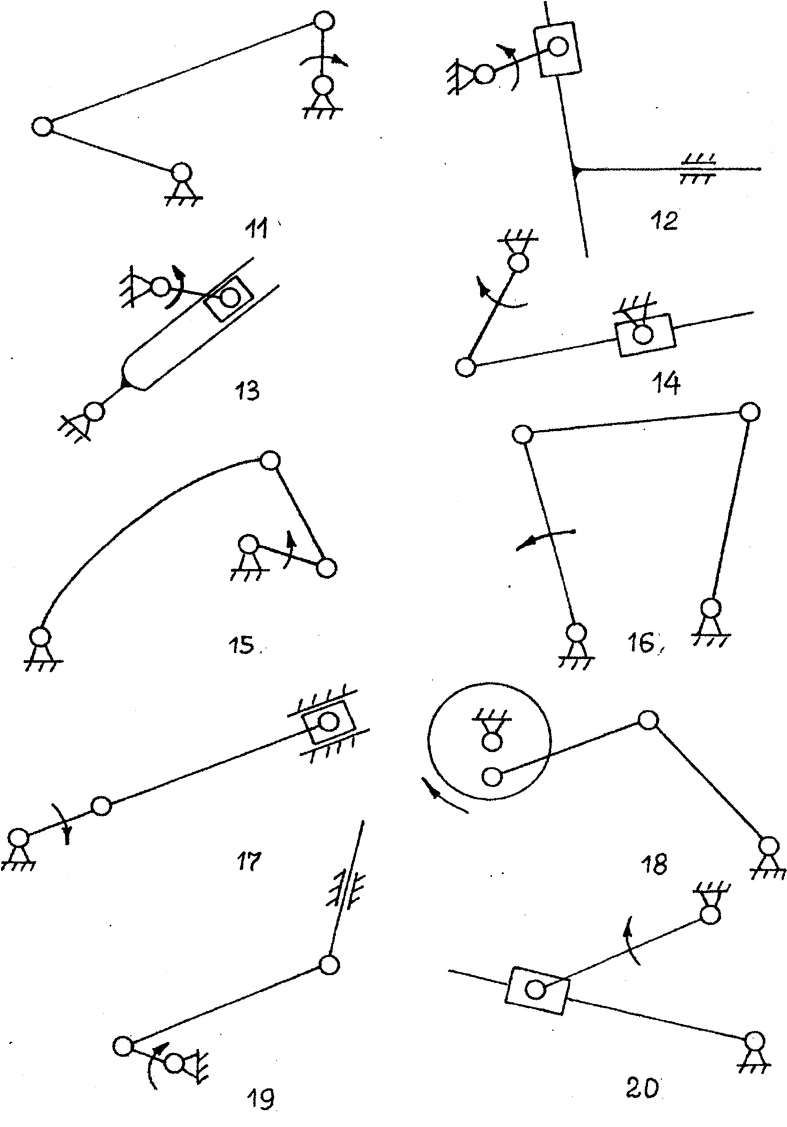
Рисунок 7 Схема плоского механизма
Структурный анализ механизма
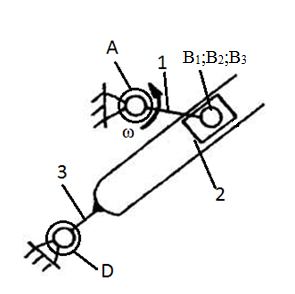
Рисунок 8 Структурный анализ механизма
Построение планов скоростей и ускорений проводится на основе последовательного составления векторных уравнений для точек звеньев механизма, начиная с ведущего звена, угловая скорость ω1 которого задана.
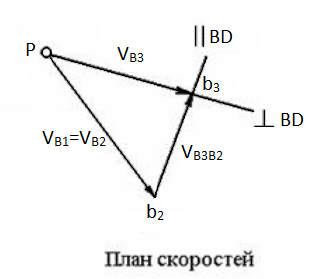
Построение плана скоростей
Скорость точки В (Рисунок 8) находится из уравнения:
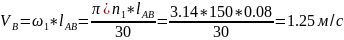
Вектор скорости точки В направлен в сторону вращения ведущего звена перпендикулярно звену АВ.
Скорость точки В2 принадлежащей камню, равна скорости В1, принадлежащей кривошипу
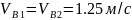
Из полюса Р плана скоростей для исходного положения механизма отложим отрезок, изображающий скорость точки В1. Пусть <pibi>=100 мм, тогда масштаб плана скоростей будет
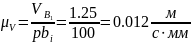
Скорость точки В3, принадлежащей кулисе 3, можно найти по векторному уравнению скоростей,
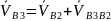
где
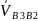 –
вектор скорости точки В3
кулисы относительно точки В2
ползуна, параллельный прямой С1D
плана механизма.
–
вектор скорости точки В3
кулисы относительно точки В2
ползуна, параллельный прямой С1D
плана механизма.
После
выбора масштаба плана скоростей
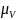 строят план скоростей. Из полюса Р
перпендикулярно отрезку АВ плана
механизма проводится вектор скорости
, совпадающий с вектором скорости. Через
точку b1
проводят прямую, параллельную прямой
С1D
, а через полюс Р – прямую, перпендикулярную
С1D.
На их пересечении получают точку b3
и наносят направление векторов (стрелки),
руководствуясь векторным уравнением
скоростей.
строят план скоростей. Из полюса Р
перпендикулярно отрезку АВ плана
механизма проводится вектор скорости
, совпадающий с вектором скорости. Через
точку b1
проводят прямую, параллельную прямой
С1D
, а через полюс Р – прямую, перпендикулярную
С1D.
На их пересечении получают точку b3
и наносят направление векторов (стрелки),
руководствуясь векторным уравнением
скоростей.
Вычисляют величины скоростей:
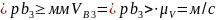
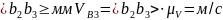
Построение плана ускорений
Исходными данными для построения плана ускорения являются план положения механизма, план скоростей и ускорения точек ведущего звена АВ.
Cоставляем векторные уравнения
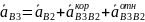
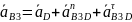
Где
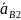 – ускорение ползуна;
– ускорение ползуна;
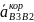 –
ускорение Кориолиса точки B3
относительно B2
(возникает тогда, когда есть относительное
движение двух точек с одновременным
вращением их вокруг какой-либо оси; в
данном случае точка B3
движется относительно B2,
вместе они вращаются вокруг неподвижной
точки D;
направление вектора
определяется так: необходимо условно
повернуть вектор скорости VB3B2
по направлению вращения кулисы 3 – это
и будет направление ускорения Кориолиса);
–
ускорение Кориолиса точки B3
относительно B2
(возникает тогда, когда есть относительное
движение двух точек с одновременным
вращением их вокруг какой-либо оси; в
данном случае точка B3
движется относительно B2,
вместе они вращаются вокруг неподвижной
точки D;
направление вектора
определяется так: необходимо условно
повернуть вектор скорости VB3B2
по направлению вращения кулисы 3 – это
и будет направление ускорения Кориолиса);
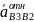 – относительное ускорение точки B3
относительно B2
(его вектор параллелен B3D);
– относительное ускорение точки B3
относительно B2
(его вектор параллелен B3D);
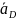 – ускорение точки D
(
– ускорение точки D
(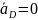 ,
так как точка D
неподвижна);
,
так как точка D
неподвижна);
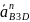 –
нормальное ускорение точки B3
относительно D
(направление вектора от B3
к точке D);
–
нормальное ускорение точки B3
относительно D
(направление вектора от B3
к точке D);
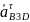 –
тангенциальное ускорение точки B3
относительно D
(вектор направлен перпендикулярно B3D).
–
тангенциальное ускорение точки B3
относительно D
(вектор направлен перпендикулярно B3D).
Вычисление величины ускорения Кориолиса и нормальных ускорений можно произвести по формулам
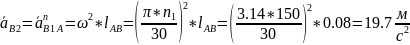
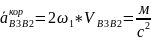
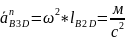
Масштаб плана ускорений выбирают, используя формулу
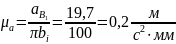
Остальные известные величины ускорений переводятся масштабом в векторные отрезки соответствующих длин:

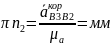
Затем
строится план ускорений. Из произвольно
выбранного полюса – точки π – проводится
вектор ускорения
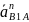 с длиной πа'2.
Из точки а'2
перпендикулярно B2D
проводится вектор ускорения
с длиной a'2k.
Через точку k
проводится прямая, перпендикулярная
этому вектору. Таким образом, будет
выполнено графическое изображение
первого векторного уравнения ускорений
из двух, ранее составленных. Затем
приступают к построению второго
векторного уравнения. Из полюса π
параллельно прямой B3D
проводится вектор ускорения длиной
πn2,
а через точку n2
– перпендикулярная ему прямая до
пересечения с прямой, проведённой ранее
через точку k.
На пересечении этих прямых получается
точка а'3.
Вектор, соединяющий точки π и а'3,
– полное ускорение аB3
точки B3.
с длиной πа'2.
Из точки а'2
перпендикулярно B2D
проводится вектор ускорения
с длиной a'2k.
Через точку k
проводится прямая, перпендикулярная
этому вектору. Таким образом, будет
выполнено графическое изображение
первого векторного уравнения ускорений
из двух, ранее составленных. Затем
приступают к построению второго
векторного уравнения. Из полюса π
параллельно прямой B3D
проводится вектор ускорения длиной
πn2,
а через точку n2
– перпендикулярная ему прямая до
пересечения с прямой, проведённой ранее
через точку k.
На пересечении этих прямых получается
точка а'3.
Вектор, соединяющий точки π и а'3,
– полное ускорение аB3
точки B3.
План механизма
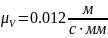
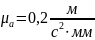
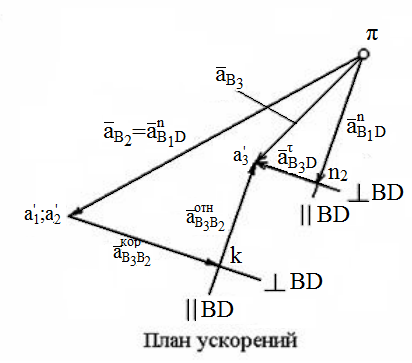
 Рисунок
9 Кинетический анализ механизма
Рисунок
9 Кинетический анализ механизма
